




|
 
|

|
1) Astronomy Picture of the Day, Tantalizing Titan, http://apod.nasa.gov/apod/ap041028.html
If you fell into Titan's atmosphere, here's what you'd see. Unlike the previous picture, this is in natural colors, taken by the Cassini probe on March 31st, 2005 from a distance of just 9,500 kilometers:
2) Wikipedia, Titan's atmosphere, http://en.wikipedia.org/wiki/Titan_(moon)#Atmosphere
The orange stuff is hydrocarbon "smog", perhaps made of chemicals called tholins which I don't really understand. When you got further down the atmosphere would be so thick, and the gravity so low, that you could fly through it by flapping wings attached to your arms. Unfortunately the atmosphere would be very cold, and unbreathable: mostly nitrogen, with a little methane and ethane. (I wrote about the hydrocarbon rain on Titan back in "week160", and showed you the first pictures of its lakes in "week210".)
Astronomy is great, but today I want to talk about group theory. As you may have heard, John Thompson and Jacques Tits won the 2008 Abel prize for their work on groups:
3) Abel Prize, 2008 Laureates, http://www.abelprisen.no/en/prisvinnere/2008/
If you want a fun, nontechnical book that gives a good taste of the sort of things Thompson thought about, try this:
4) Marcus du Sautoy, Symmetry: a Journey into the Patterns of Nature, HarperCollins, 2008.
Mathematicians will enjoy this book for its many anecdotes about the heroes of symmetry, from Pythagoras to Thompson and other modern group theorists. Nonmathematicians will learn a lot about group theory in a fun easy way.
As a PhD student working under Saunders Mac Lane, Thompson began his career with a bang, by solving a 60-year-old conjecture posed by the famous group theorist Frobenius.
5) Mactutor History of Mathematics Archive, John Griggs Thompson, http://www-history.mcs.st-andrews.ac.uk/Biographies/Thompson_John.html
But, he's mainly famous for helping prove an even harder theorem that's even simpler to state - one of those precious nuggets of knowledge that mathematicians fight so hard to establish:
We say a group is "solvable" if it can be built out of abelian groups in finitely many stages: the group at each stage mod the group at the previous stage must be abelian. The term "solvable" comes from Galois theory, since we can solve a polynomial equation using radicals iff its Galois group is solvable.
Way back in 1911, Burnside conjectured that every finite group with an odd number of elements is solvable. John Thompson and Walter Feit proved this in 1963. Their proof took all 255 pages of an issue of the Pacific Journal of Mathematics!
The proof has been simplified a bit since then, but not much. Versions can be found in two different books, and there is a project underway to verify it by computer:
6) Wikipedia, Feit-Thompson Theorem, http://en.wikipedia.org/wiki/Feit-Thompson_theorem
This theorem, also called the "odd order theorem", marked a trend toward really long proofs in finite group theory, as part of a quest to classify finite "simple" groups. A simple group is one that has no nontrivial normal subgroups. In other words: there's no way to find a smaller group inside it, mod out by that, and get another smaller group. So, more loosely speaking, we can't build it up in several stages: it's a single-stage affair, a basic building block.
One reason finite simple groups are important is that every finite group can be built up in stages, where the group at each stage mod the group at the previous stage is a finite simple group. So, the finite simple groups are like the "prime numbers" or "atoms" of finite group theory.
The first analogy is nice because abelian finite simple groups practically are prime numbers. More precisely, every abelian finite simple group is Z/p, the group of integers mod p, for some prime p. So, building a finite group from simple groups is a grand generalization of factoring a natural number into primes.
However, the second analogy is nice because just as you can build different molecules with the same collection of atoms, you can build different finite groups from the same finite simple groups.
I actually find a third analogy helpful. As I hinted, for any finite group we can find an increasing sequence of subgroups, starting with the trivial group and working on up to the whole group, such that each subgroup mod the previous one is a finite simple group. So, we're building our group as a "layer-cake" with these finite simple groups as "layers".
But: knowing the layers is not enough: each time we put on the next layer, we also need some "frosting" or "jam" to stick it on! Depending on what kind of frosting we use, we can get different cakes!
To complicate the analogy, stacking the layers in different orders can sometimes give the same cake. This is reminiscent of how multiplying prime numbers in different orders gives the same answer. But, unlike multiplying primes, we can't always build our layer cake in any order we like.
Apart from the order, though, the layers are uniquely determined - just as every natural number has a unique prime factorization. This fact is called the "Jordan-Hölder theorem", and these layer cakes are usually called "composition series". For more, try this:
7) Wikipedia, Composition series, http://en.wikipedia.org/wiki/Composition_series
But let's see some examples!
Suppose we want to build a group out of just two layers, where each layer is the group of integers mod 3, otherwise known as Z/3. There are two ways to do this. One gives Z/3 ⊕ Z/3, the group of pairs of integers mod 3. The other gives Z/9, the group of integers mod 9.
We can think of Z/3 ⊕ Z/3 as consisting of pairs of digits 0,1,2 where we add each digit separately mod 3. For example:
01 + 02 = 00
12 + 11 = 20
11 + 20 = 01
We can think of Z/9 as consisting of pairs of digits 0,1,2 where we add each digit mod 3, but then carry a 1 from the 1's place to the 10's place when the sum of the digits in the 1's place exceeds 2 - just like you'd do when adding in base 3. I hope you remember your early math teachers saying "don't forget to carry a 1!" It's like that. For example:
01 + 02 = 10
12 + 11 = 00
11 + 20 = 01
So, the "frosting" or "jam" that we use to stick our two copies of Z/3 together is the way we carry some information from one to the other when adding! If we do it trivially, not carrying at all, we get Z/3 ⊕ Z/3. If we do it in a more interesting way we get Z/9.
In fact, this how it always works when we build a layer cake of groups. The frosting at each stage tells us how to "carry" when we add. Suppose at some stage we've got some group G. Then we want to stick on another layer, some group H. An element of the resulting bigger group is just a pair (g,h). But we add these pairs like this:
(g,h) + (g',h') = (g + g' + c(h,h'), h + h')
where
c: H × H → G
tells us how to "carry" from the "H place" to the "G place" when we add. So, information percolates down when we add two guys in the new top layer of our group.
Of course, not any function c will give us a group: we need the group laws to hold, like the associative law. To make these hold, the function c needs to satisfy some equations. If it does, we call it a "2-cocycle".
These cocycles are studied in a subject called "group cohomology". Usually people focus on the simplest case, when our original group G is abelian, and its elements commute with everything in the big new group we're building. If this isn't true, we need something more general: nonabelian group cohomology, often called "Schreier theory" (see "week223").
I like this layer cake business because it's charming and it generalizes in two nice ways. First of all, it works for lots of algebraic gadgets besides groups. Second of all, it works for categorified versions of these gadgets.
For example, a group is a category with one object, all of whose morphisms are invertible. Similarly, an "n-group" is an n-category with one object, all of whose 1-morphisms, 2-morphisms and so on are invertible. We can build up n-groups as layer cakes where the layers are groups. It's a more elaborate version of what I just described - and it uses not just "2-cocycles" but also "3-cocycles" and so on. I never really understand group cohomology until I learned to see it this way.
But what's really cool is that n-groups can also be thought of as topological spaces. This lets us build every space as a "layer cake" where the layers are groups! These groups are called the "homotopy groups" of the space. The nth homotopy group keeps track of how many n-dimensional holes the space has - see "week102" for details.
But of course, they don't call the process of sticking these groups together a "layer cake": that would be too undignified. They call it a "Postnikov tower". And instead of "frosting", they speak of "Postnikov invariants". Every space is the union of a bunch of connected pieces, each of which is determined by its homotopy groups and its Postnikov invariants.
(At least this is true if you count spaces as the same when they're "weakly homotopy equivalent". This is a fairly sloppy equivalence relation beloved by homotopy theorists. You've probably heard how a topologist is someone who can't tell the difference between a doughnut and a coffee cup. Actually they can tell: they just don't care! A homotopy theorist is a more relaxed sort of guy who doesn't even care about the difference between a doughnut and a Moebius strip. They're both just fattened up versions of a circle.)
Mike Shulman and I tried to explain this layer cake business here:
8) John Baez and Michael Shulman, Lectures on n-categories and cohomology, to appear in n-Categories: Foundations and Applications, eds. John Baez and Peter May. Also available as arXiv:math/0608420
Whoops! I see I've drifted from my supposed topic - the work of John Thompson - to something I actually understand. It was a digression, but not a completely pointless one. From what I've told you, it follows that every space with finite homotopy groups can be built as a fancy "layer cake" made of finite simple groups.
And even better, the finite simple groups have now been classified! - we think. There are 18 infinite series of these groups, and also 26 exceptions called "sporadic" groups, ranging in size from the five Mathieu groups (see "week234") on up to the Monster (see "week20" and "week66").
9) Wikipedia, List of finite simple groups, http://en.wikipedia.org/wiki/List_of_finite_simple_groups
Proving that these are all the possibilities took mathematicians about 10,000 pages of work! The Feit-Thompson theorem is a small but crucial piece in this enormous pyramid of proofs. There could still be some mistakes here and there, but experts are busy working through the details more carefully.
Among the 26 sporadic groups, one is called the Thompson group. It was discovered by Thompson, and it's a subgroup of a version of the group E8 defined over F3, the field with 3 elements. It has about 9 × 1016 elements, and it has a 248-dimensional representation over F3. I don't know much about it. I mention it just to show what crazy possibilities had to be considered to classify all finite simple groups - and how deeply Thompson was involved in this work.
But what about Jacques Tits?
10) Mactutor History of Mathematics Archive, Jacques Tits http://www-history.mcs.st-andrews.ac.uk/Biographies/Tits.html
He's not mentioned in du Sautoy's book "Symmetry", which is a pity, but not surprising, since too many mathematicians have studied group theory to fit comfortably in one story. He has a sporadic finite simple group named after him, but his work leaned in a different direction, more focused on the role of groups in geometry. He was an honorary member of Bourbaki, and in that role he helped awaken interest in the work of Coxeter.
I've mentioned his work on the "magic square" of exceptional Lie groups in "week145" and "week253"... but he's more famous for his work on "buildings", sometimes called "Bruhat-Tits buildings".
The subject of buildings has a reputation for being intimidating, perhaps because the definition of a building looks scary and unmotivated. You can read these and decide for yourself:
11) Wikipedia, Building (mathematics), http://en.wikipedia.org/wiki/Building_%28mathematics%29
12) Kenneth S. Brown, What is a building?, Notices AMS, 49 (2002), 1244-1245. Also available at http://www.ams.org/notices/200210/what-is.pdf
13) Paul Garrett, Buildings and Classical Groups, CRC Press, 1997. Preliminary version available at http://www.math.umn.edu/~garrett/m/buildings/
14) Kenneth S. Brown, Buildings, Springer, 1989.
15) Mark Ronan, Lectures on Buildings, Academic Press, 1989.
Personally I found it a lot easier to start with examples.
So, start with any "finite reflection group" - a finite group of transformations of Rn that's generated by reflections. The possibilities have been completely worked out, and I listed them back in "week62". But let's do an easy one: the symmetry group of an equilateral triangle.
I can't resist mentioning that this group is also S3, the group of all permutations of the three vertices of the triangle. In fact, this group was the star of "week261", where it showed up as the Galois group of the cubic equation! We can solve a cubic using radicals since this group is solvable. In other words, we can build this group as a "layer cake" from the abelian groups Z/3 and Z/2. The bottom layer is Z/3, the subgroup of even permutations. The top layer is S3 modulo the even permutations, namely Z/2. Galois theory says you can solve a cubic by messing around a bit, then taking a square root, and then taking a cube root. Why a square root first? Because you build this sort of layer cake from the bottom up, but you eat it from the top down, slicing off one layer at a time.
But now we want to think about how this group is generated by reflections. You can use just two, for example the reflections across the mirrors labelled r and s here:
s
\ /
\ /
\ /
\ /
--------o--------r
/ \
/ \
/ \
/ \
Let's call these reflections r and s. They clearly satisfy
r2 = s2 = 1
but since the mirrors are at an angle of π/3 from each other, they also satisfy
(rs)3 = 1
This gives a presesentation of our group S3. We can summarize this presentation with a little "Coxeter diagram":
3
r-------s
where the dots r and s are the generators, and the edge labelled
"3" is the interesting relation (rs)3 = 1. I
explained these diagrams more carefully back in "week62". If you know about Dynkin diagrams,
these are pretty similar - see "week63" and "week64" for details.
Note that the mirrors in this picture:
s
\ /
\ /
\ /
\ /
--------o--------r
/ \
/ \
/ \
/ \
chop the plane into
6 "chambers", and the group S3 has 6
elements. This is no coincidence - it works like this for any finite
reflection group! We can pick any chamber as our favorite and label
it 1:
s
\ /
\ /
\ / 1
\ /
--------o--------r
/ \
/ \
/ \
/ \
Then, we can label any other chamber by the unique element of
our group that carries our favorite chamber to that one:
s
\ /
\ s /
sr \ / 1
\ /
--------o--------r
/ \
rsr = srs / \ r
/ rs \
/ \
If we start with chamber 1 and keep reflecting across mirrors,
we keep getting products of more and more generators until we
reach the diametrically opposite chamber, which corresponds to
the so-called "long word" in our finite reflection group. In
this case, the long word is rsr = srs.
(Fanatical devotees will also note that this equation is the "Yang-Baxter equation" mentioned in "week261".)
Now, Coxeter thought about all this stuff, and he realized that it was nice to introduce a polytope with one face for each chamber - in this case, just a hexagon:
s
o-----o
rs / \1
/ \
o o
\ /
rsr \ /r
o-----o
sr
This is called the "Coxeter complex" of our finite reflection
group. Our finite reflection group acts on it, and it acts
on the faces in a free and transitive way.
But, you'll note we started with the symmetry group of an equilateral triangle, and wound up with a hexagon! What happened?
The quick way to say it is this: combinatorially speaking, the hexagon is the "barycentric subdivision" of our original triangle. Not the inside of the triangle - just its surface, or boundary! The boundary of the triangle is a simplicial complex made of 3 vertices and 3 edges:
o
. .
. .
. o
. .
. .
o
so if we barycentrically subdivide it, we get 6 vertices
and 6 edges:
o-----o
/ \
/ \
o o
\ /
\ /
o-----o
and that's our hexagon - drawn puffed out a bit, just for the sake
of prettiness.
If this seems bizarre - and it probably does, given how lousy these pictures are - I urge you to try the next example on your own. Take the symmetry group of the regular tetrahedron, also known as S4, the group of permutations of 4 things. Show it's generated by three reflections r,s,t with relations
r2 = s2 = t2 = 1
(rs)3 = (st)3 = 1
rt = tr
We can summarize these with the following Coxeter diagram:
3 3
r-------s-------t
Draw all mirrors corresponding to reflections in S4, and show
they chop 3d space into 24 chambers, one for each element of S4.
Then, barycentrically subdivide the boundary of the tetrahedron
and check that the resulting "Coxeter complex" has 24 faces, one
inside each chamber.
Anyway, one thing Tits did is realize how these Coxeter complexes show up in the geometry of the Lie groups, or more generally algebraic groups, associated to Dynkin diagrams.
For example, if I take this guy:
3
r-------s
and remove some of the labels, I get the so-called A2
Dynkin diagram:
o-------owhich corresponds to the Lie group PSL(3). And, this is the group of symmetries of projective plane geometry! Each dot in the Dynkin corresponds to a "type of figure":
POINT LINE o-------oand the edge corresponds to an "incidence relation": in projective plane geometry, a point can lie on a line. This shape, which we've seen before:
o
. .
. .
. o
. .
. .
o
is then revealed to stand for a configuration of 3 points and 3
lines, satisfying incidence relations obvious from the picture.
To put points and lines on an equal footing, we switch to the
the Coxeter complex:
POINT LINE
o-----o
/ \
/ \
LINE o oPOINT
\ /
\ /
o-----o
POINT LINE
where now the vertices represent "figures" and the edges represent
"incidence relations". It turns out that inside any projective
plane, we can find lots of configurations like this: 3 points and
3 lines, each pair of points lying on one of the lines, and each
pair of lines intersecting in a point. Such a configuration is
called an "apartment".
If we take all the apartments coming from a projective plane, they form a simplicial complex called a "building". And this generalizes to any geometry corresponding to any sort of Dynkin diagram. The building knows everything about the geometry: all the figures, all the incidence relations.
And that's all I have time for now, but it's just the beginning of the marvelous theory Jacques Tits worked out.
Addenda: At least on Titan, tholins seem to be a complex brew of compounds made by irradiation of molecular nitrogen and methane in the upper atmosphere. The same sort of compounds could be an early chemical step in the formation of life on Earth - that's one reason I'm interested. They're related to PAHs, or "polycyclic aromatic hydrocarbons", which are ubiquitous in outer space - I wrote about those back in "week258". I guess the main difference is that tholins contain nitrogen!
I found some more information on tholins here:
16) J. H. Waite, Jr., et al, The process of tholin formation in Titan's upper atmosphere, Science 316 (2007), 870-875.
Here's a picture of how tholins get made, from this paper:
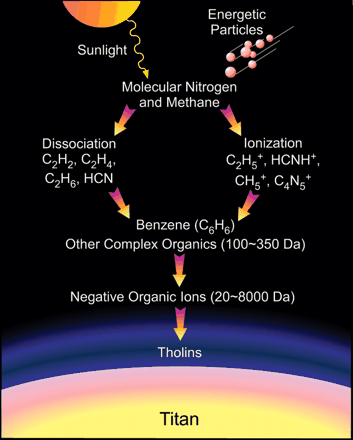
You can see more discussion and also questions I'm dying to know the answers to over at the n-Category Café. Whenever I write This Week's Finds, I come up with lots of questions. If you can help me with some of these, I'll be really grateful.
© 2008 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|