August 30, 2008

This Week's Finds in Mathematical Physics (Week 269)

John Baez

No fancy math today. I've been working hard with Aristide Baratin, Laurent Freidel and Derek Wise on infinite-dimensional representations of 2-groups. It's a gnarly mix of higher category theory and analysis. But I won't bother you with that until the paper is done. I need a break!

So, today I want to talk about the sulfur geysers on Io, honeycombs, the work of Kelvin, the Weaire-Phelan structure, and gas clathrates.

I already teased you with pictures of Jupiter's moon Io in "week266" and "week268". There's a reason. Tortured by powerful tidal forces, Io is the most geologically active object in the Solar System! It has mountains taller than Mount Everest, and over 400 active volcanos. These put out the hottest lava ever seen - and a lot of it, too. A big eruption in 1997 produced more than 3500 square kilometers of the stuff!

Most moons in the outer Solar System are pale and icy. Io looks like an evil pizza. The ghastly red ring in the top view here is sulfur spewed out by Pele, the biggest volcano on Io:

1) NASA Photojournal, Three views of Io, http://photojournal.jpl.nasa.gov/catalog/PIA00292

Io is big on sulfur. It has lakes of molten sulfur... pale sulfur dioxide snow... and geysers spew sulfur dioxide up to 500 kilometers high! Here's a picture of two such geysers, taken by the Galileo spacecraft in 1997:

2) Astronomy Picture of the Day, Io: the Prometheus plume, http://apod.nasa.gov/apod/ap070211.html

At the top horizon you can see a cloud of bluish-white haze. It may not look big, but remember: Io is about 3600 kilometers in diameter, roughly the size of our Moon. So, that hazy cloud is actually huge. It's a geyser plume rising 140 kilometers above a massive volcano called Pillan Patera. If you look carefully you can also see the Prometheus plume, dead center, as a blue-grey ring. This plume has been active at least since 1979 - but it's moved 85 kilometers west during that time! Scary.

Ironically, all this chaotic activity on Io may be caused by the "music of the spheres". Io is locked in a 2:1 orbital resonance with the moon Europa, and a 4:1 resonance with Ganymede. These keep Io's orbit a bit eccentric, which causes tidal heating - to the tune of about 100 trillion watts.

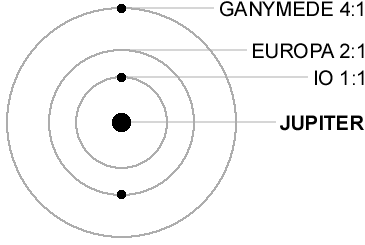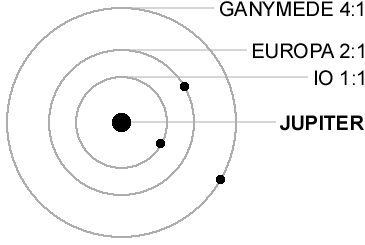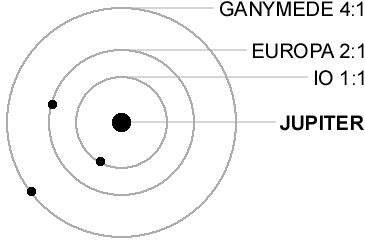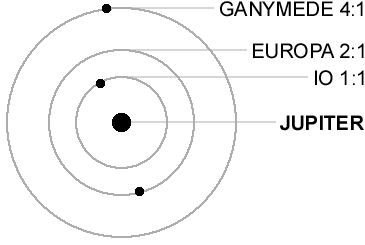
Another interesting thing is that the red spots on Io are made of sulfur, but so are the yellow plains. Of course there are lots of compounds involving sulfur, but even the pure element has a lot of different forms, or allotropes. I've always been fascinated by those.

Back here on Earth, the Weaire-Phelan structure was in the news recently! If you watched the Olympics in Beijing, you may have seen the National Aquatics Center - a building also called the "Water Cube":

3) Spectacular mathematical bubble design at the Olympics, Math in the News, Mathematical Association of America, August 8, 2008, http://mathdl.maa.org/mathDL?pa=mathNews&sa=view&newsId=392

The design of this building is based on the Weaire-Phelan structure. But the story behind the design of this building goes back to 36 BC, when Marcus Terentius Varro described two competing theories for why bees have hexagonal honeycombs. The first said: because bees have six legs! The second said: efficiency! You see, a hexagonal lattice lets you divide the plane into cells of equal area with the least possible perimeter per cell. So if the bees want to save wax, that's the pattern they'll pick.

The second theory seems more plausible. But is it true? I'm not even sure how to resolve that question. But it's worth noting that honeycomb cells are actually 3-dimensional - and the end of each cell consists of three rhombi that meet at the same angle as bubbles in soap suds!

Now, soap films minimize surface area subject to whatever constraints they encounter. So, a single bubble that holds a given amount of air will form a sphere. But soap suds with lots of bubbles do more complicated things. Take a bubble bath and pay careful attention! You'll see that three bubble faces meet along each edge, at precisely 120 degree angles. And when four bubbles meet at a vertex, they form a pattern with tetrahedral symmetry, with edges meeting at an angle of arccos(-1/3), or about 109.5 degrees.

So if honeycombs display these patterns, we can guess area is being minimized.

But as usual, things get more complicated when you look deeper. First, while everyone believed for a long time that a hexagonal honeycomb is the way to divide the plane into equal-area cells with minimal perimeters, this was only proved much later: in 1999, by Thomas Hales.

It's an interesting story. Hales had just finished his epic proof of Kepler's conjecture about the densest way to pack equal-sized spheres - a proof so complicated that the referees "ran out of energy" trying to check it. That's quite a tale in itself... but to avoid an infinite sequence of nested digressions, I'll refer you to these:

4) George G. Szpiro, Kepler's Conjecture, John Wiley and Sons, 2003. Reviewed by Frank Morgan in Notices Amer. Math. Soc. 52 (2005), 44-47. Also available at http://www.ams.org/notices/200501/rev-morgan.pdf

5) Thomas Hales, The Kepler Conjecture, http://www.math.pitt.edu/~thales/kepler98/

Anyway, after Hales proved the Kepler Conjecture, Denis Weaire suggested that he tackle the Hexagonal Honeycomb Conjecture - and Hales promptly solved that too! He said, "In contrast with the years of forced labor that gave the Kepler Conjecture, I felt as if I had won the lottery."

6) Thomas C. Hales, The Honeycomb Conjecture, http://www.math.pitt.edu/~thales/kepler98/honey/

Hales wasn't the first to make progress on the Hexagonal Honeycomb Conjecture. A guy named Fejes Tóth had already proved it's true if we assume the cells are polygons:

7) L. Fejes Tóth, Regular Figures, Macmillan, New York, 1964.

So what Hales had to do is rule out cells with curved edges. This is harder than you might think. In fact, for clusters of finitely many cells, the optimal shapes can be curved, even near the middle!

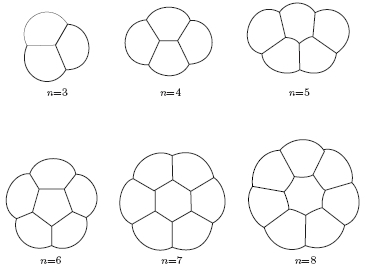
7) S. J. Cox, M. Fatima Vas, C. Monnereua-Pittet and N. Pittet, Minimal perimeter for N identical bubbles in two dimensions: calculations and simulations, Phil. Mag. 83 (2003), 1393-1406.

Another thing Tóth did is carefully define the 3d optimization problem that bees might be trying to solve, and find a slightly better solution:

9) L. Fejes Tóth, What the bees know and what the bees do not know, Bull. Amer. Math. Soc. 70 (1964), 468-481. Also available at http://projecteuclid.org/euclid.bams/1183526078

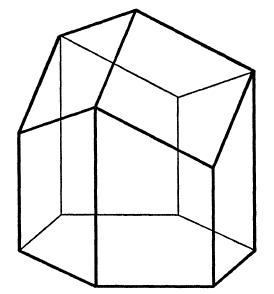
I won't try to describe his results in detail, since the paper is freely available and well-written. But here's the basic idea. The end of a bee's honeycomb cell looks just like a corner of a rhombic dodecahedron:

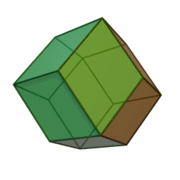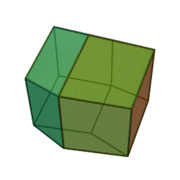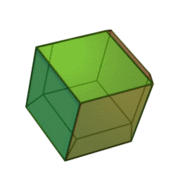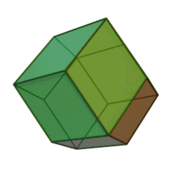
This is a 12-sided solid that you can pack to completely fill space. This makes sense, because the ends of one layer of cells in a honeycomb should neatly fit against those of the next layer.

However, it's been known since the work of Kelvin that there's another solid you can use to pack space more efficiently: that is, with less surface area per cell. This is the truncated octahedron:

Using this, Tóth found a design for the end of a honeycomb cell that would be more efficient than what bees use:

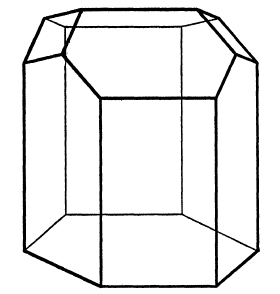
How much more efficient? How much area did Tóth manage to shave off? Almost 0.35% of the area of cell's opening! In the eternal battle of man against bee, we triumph yet again! It makes me proud to be human.

Tóth is more modest:

We must admit that all this has no practical consequence.... Besides, the building style of the bees is definitely simpler than that described above. So we would fail in shaking someone's conviction that the bees have a deep geometrical intuition.

Now, back to Kelvin! When he bumped into the truncated octahedron, he was actually studying the 3d version of the 2d Hexagonal Honeycomb Conjecture. In other words, he was trying to chop 3d space into cells of equal volume with the least surface area per cell. And he conjectured that the answer was very similar to filling space with truncated octahedra, as shown here:

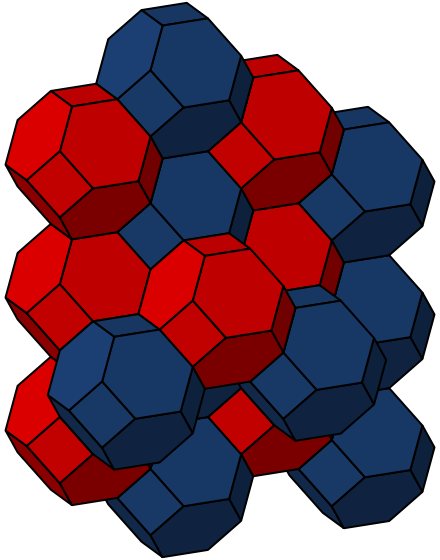
9) Wikipedia, Bitruncated cubic honeycomb, http://en.wikipedia.org/wiki/Bitruncated_cubic_honeycomb

I say "very similar" because it's actually more efficient if you let the hexagonal faces in this structure be slightly curved. So, the possibility Hales ruled out in the 2d case actually matters here! In his 1887 paper on this subject, Kelvin wrote:

No shading could show satisfactorily the delicate curvature of the hexagonal faces, though it may be fairly well seen on the solid model made as described in Section 12. But it is shown beautifully, and illustrated in great perfection, by making a skeleton model of 36 wire arcs for the 36 edges of the complete figure, and dipping it in soap solution to fill the faces with film, which is easily done for all the faces but one. The curvature of the hexagonal film on the two sides of the plane of its six long diagonals is beautifully shown by reflected light.

You can read Kelvin's paper here:

10) Lord Kelvin, On the division of space with minimum partitional area, Phil. Mag. 24 (1887), 503. Also available at http://zapatopi.net/kelvin/papers/on_the_division_of_space.html

His lively mind is evident from the selection of papers on this site. For example: "On Vortex Atoms", where he unsuccessfully tried to build atoms out of knotted electromagnetic field lines, and wound up giving birth to knot theory. Some others I hadn't heard of: "On the origin of life", "The sorting demon of Maxwell", and "Windmills must be the future source of power".

Anyway: for over a century the so-called "Kelvin structure" was believed to be the best solution to the problem of chopping space into equal volume cells with minimal surface area. But in 1993 two physicists at Trinity College in Dublin - Denis Weaire and Robert Phelan - found a solution that has 0.3% less surface area! It looks like this:

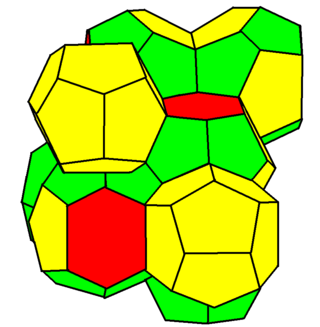
11) Wikipedia, Weaire-Phelan structure, http://en.wikipedia.org/wiki/Weaire–Phelan_structure

It's built from two kinds of cells - a 12-sided one and a 14-sided one. Was that allowed in Kelvin's original puzzle? I can't tell!

In fact, this so-called "Weaire-Phelan structure" was no bolt out of the blue. The basic pattern had already been seen in certain cage-like crystals called "clathrates". For example, down at the bottom of the ocean there's somewhere between 500 and 2500 billion tons of methane hydrate, a funny substance in which methane molecules are trapped in polyhedral cages formed by water molecules. It looks like ice, but you can ignite it with a cigarette lighter! If you think global warming is bad now, just wait until people figure out how to mine this stuff....

Anyway, methane hydrate is just one of a collection of gas hydrates with different geometries. And it's an example of a "type I" gas hydrate, where water molecules form cages patterned after the Weaire-Phelan structure!

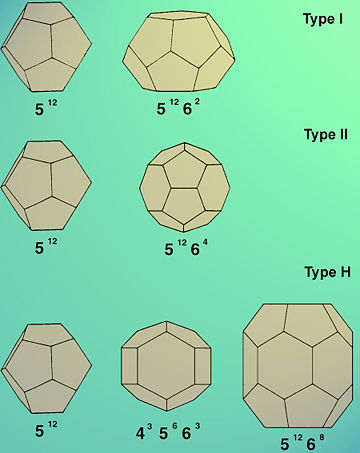
12) Wikipedia, Clathrate hydrate, http://en.wikipedia.org/wiki/Clathrate_hydrate

So, it's nicely appropriate to use the Weaire-Phelan structure for a building called the Water Cube. Since this structure is perfectly periodic, the engineer for the Water Cube cut it at an odd angle to make it look more exciting. The MAA article cited above says:

Made of a plastic known as ethylene tetrafluoroethylene and filled with air, the bubbles are attached to a steel framework outlining the bubble edges. Surface tension holds the bubbles together and tends to pull them into a structure with least surface area.

The building "really looks like nothing else in the world," Tristam Carfrae told the New York Times. "It's a box made of bubbles." Carfrae is the structural engineer who designed the center.

On the math side of things, there's plenty left to be done. Nobody has proved that the Weaire-Phelan structure is the best solution to Kelvin's problem. According to Frank Morgan, the expert on minimal surface who reviewed Spziro's book on Kepler's problem,

Proving the Weaire-Phelan structure optimal looks perhaps a century beyond current mathematics to me, but I understand that Hales is already thinking about it.

13) Frank Morgan, Geometric Measure Theory: a Beginner's Guide, Academic Press, New York, 2000.

Personally, I'm more in love with symmetry than minimization. So, I want to learn more about the 28 "convex uniform honeycombs" - ways of uniformly packing 3d space with uniform solids:

14) Wikipedia, Convex uniform honeycomb, http://en.wikipedia.org/wiki/Convex_uniform_honeycomb

They're related to Coxeter groups and "crystallographic groups", which are the 3d analogues of the wallpaper groups I discussed back in "week267". In fact, we can study honeycombs and their symmetry groups in any dimension, both in flat space and in positively curved (spherical) and negatively curved (hyperbolic) space. A lot is known about them....

Addenda: I thank Jim Stasheff and Mike Stay for drawing my attention to the Water Cube and its use of the Weaire-Phelan structure. I thank Blake Stacey for catching a mistake.

My suggestion is that Aepinus' fluid consists of exceedingly minute equal and similar atoms, which I call electrions, much smaller than the atoms of ponderable matter. - Lord Kelvin, Aepinus Atomized

One word characterizes the most strenuous effors for the advancement of science I have made perserveringly during fifty-five years; that word is Failure. I know no more of electric or magnetic force, or of the relation between ether, electricity and ponderable matter, or of chemical affinity, than I knew and tried to teach to my students of natural philosophy fifty years ago in my first session as professor. - Lord Kelvin, at a celebration of his life's work attended by more than 2000 guests

© 2008 John Baez
baez@math.removethis.ucr.andthis.edu