




|
 
|

|
This Week will be all about Frobenius algebras and modular tensor categories. But first, here's a beautiful photo of Io, the volcanic moon of Jupiter that I introduced back in "week266":
1) NASA Photojournal, A new year for Jupiter and Io, http://photojournal.jpl.nasa.gov/catalog/PIA02879
Io looks awfully close to Jupiter here! It's actually 2.5 Jupiter diameters away... but that's close enough to cause the intense tidal heating that leads to sulfur volcanoes.
I told you about Frobenius algebras in "week174" and "week224", but I think it's time to talk about them again! In the last few weeks, I've run into them - and their generalizations - in a surprising variety of ways.
First of all, Jamie Vicary visited me here in Paris and explained how certain Frobenius algebras can be viewed as classical objects living in a quantum world - governed by quantum logic.
Mathematicians in particular are used to thinking of the quantum world as a mathematical structure resting on foundations of classical logic: first comes set theory, then Hilbert spaces on top of that. But what if it's really the other way around? What if classical mathematics is somehow sitting inside quantum theory? The world is quantum, after all.
There are a couple of papers so far that discuss this provocative idea:
2) Bob Coecke and Dusko Pavlovic, Quantum measurements without sums, in The Mathematics of Quantum Computation and Technology, eds. Chen, Kauffman and Lomonaco, Chapman and Hall/CRC, New York, pp. 559-596. Also available as arXiv:quant-ph/0608035.
3) Jamie Vicary, Categorical formulation of quantum algebras, available as arXiv:0805.0432.
Second, Paul-André Melliès, the computer scientist and logician who's my host here, has been telling me how logic can be nicely formulated in certain categories - "*-autonomous categories" - which can be seen as categorified Frobenius algebras. Here the idea goes back to Ross Street:
4) Ross Street, Frobenius monads and pseudomonoids, J. Math. Physics 45 (2004) 3930-3948. Available as http://www.math.mq.edu.au/~street/Frob.pdf
Paul-André is teaching a course on this and related topics; you can see the slides for his course here:
5) Paul-André Melliès, Groupoides quantiques et logiques tensorielles: une introduction, course notes at http://www.pps.jussieu.fr/~mellies/teaching.html
See especially the fourth class.
But to get you ready for this material, I should give a quick introduction to the basics!
If you're a normal mathematician, the easiest definition of "Frobenius algebra" is something like this. For starters, it's an "algebra": a vector space with an associative product that's linear in each argument, and an identity element 1. But what makes it "Frobenius" is that it's got a nondegenerate bilinear form g satisfying this axiom:
g(ab,c) = g(a,bc)
I'm calling it "g" to remind geometers of how nondegenerate bilinear forms are used as "metrics", like the metric tensor at a point of a Riemannian or Lorentzian manifold. But beware: we'll often work with complex instead of real vector spaces. And, we won't demand that g(a,b) = g(b,a), though this holds in many examples.
Let's see some examples! For starters, we could take the algebra of n × n matrices and define
g(a,b) = tr(ab)
where "tr" is the usual trace. Or, we could perversely stick any nonzero number in this formula, like
g(a,b) = -37 tr(ab)
Or, we could take a bunch of examples like this and take their direct sum. This gives us the most general "semisimple" Frobenius algebra.
So, semisimple Frobenius algebras are pathetically easy to classify. There's also a vast wilderness of non-semisimple ones, which will never be classified. But for a nice step in this direction, try Prop. 2 in this paper:
6) Steve Sawin, Direct sum decompositions and indecomposable TQFTs, J. Math. Phys. 36 (1995) 6673-6680. Also available as q-alg/9505026.
This classifies all commutative Frobenius algebras that are "indecomposable" - not a direct sum of others.
Note the mention of topological quantum field theories, or TQFTs. Here's why. Suppose you have an n-dimensional TQFT. This gives vector spaces for (n-1)-dimensional manifolds describing possible choices of "space", and operators for n-dimensional manifolds going between these, which describe possible choices of "spacetime".
So, it gives you some vector space for the (n-1)-sphere, say A. And, this vector space is a commutative Frobenius algebra!
Let me sketch the proof. I'll use lots of hand-wavy reasoning, which is easy to make rigorous using the precise definition of a TQFT.
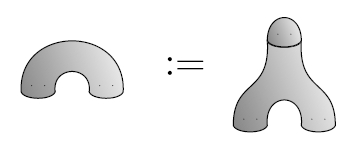
For starters, there's the spacetime where two spherical universes collide and fuse into one. Here's what it looks like for n = 2:
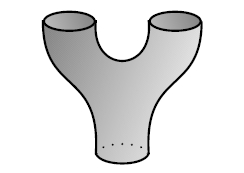
This gives the vector space A a multiplication:
m: A ⊗ A → A a ⊗ b |→ ab
Next there's the spacetime where a spherical universe appears from nothing - a "big bang":

This gives A an identity element, which we call 1:
i: C → A 1 |→ 1Here C stands for the complex numbers, but mathematicians could use any field.
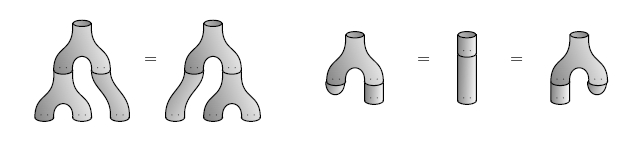
Now we can use topology to show that A is an algebra - namely, that it satisfies the associative law:
(ab)c = a(bc)
and the left and right unit laws:
1a = a = 1
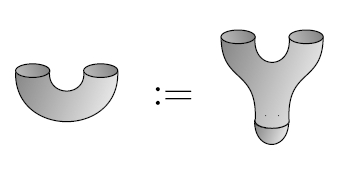
But why is it a Frobenius algebra? To see this, let's switch the future and past in our previous argument! The spacetime where a spherical universe splits in two gives A a "comultiplication":
Δ: A → A ⊗ A
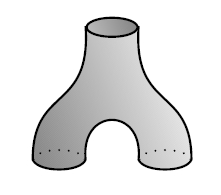
The spacetime where a spherical universe disappears into nothing - a "big crunch" - gives A a trace, or more precisely a "counit":
e: A → C
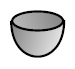
And, a wee bit of topology shows that these make A into a "coalgebra", satisfying the "coassociative law" and the left and right "counit laws":
Everything has just been turned upside down!
It's easy to see that the multiplication on A is commutative, at least for n > 1:
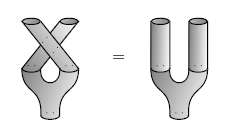
Similarly, the comultiplication is "cocommutative" - just turn the above proof upside down!
But why is A a Frobenius algebra? The point is that the algebra and coalgebra structures interact in a nice way. We can use the product and counit to define a bilinear form:
g(a,b) = e(ab)
This is just what we did in our matrix algebra example, where e was a multiple of the trace.
We can also think of g as a linear operator
g: A ⊗ A → C
But now we see this operator comes from a spacetime where two universes collide and then disappear into nothing:
To check the Frobenius axiom, we just use associativity:
g(ab,c) = e((ab)c) = e(a(bc)) = g(a,bc)

But why is g nondegenerate? I'll just give you a hint. The bilinear form g gives a map from A to the dual vector space A*:
a |→ g(a,-)
Physicists would call this map "lowering indices with the metric g". To show that g is nondegenerate, it's enough to find an inverse for this map, which physicists would call "raising indices". This should be a map going back from A* to A. To build a map going back like this, it's enough to get a map
h: C → A ⊗ A
and for this we use the linear operator coming from this spacetime:
The fact that "raising indices" is the inverse of "lowering indices" then follows from the fact that you can take a zig-zag in a piece of pipe and straighten it out!
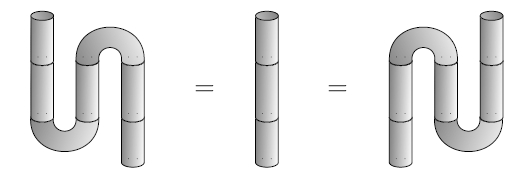
So, any n-dimensional TQFT gives a Frobenius algebra, and in fact a commutative Frobenius algebra for n > 1.
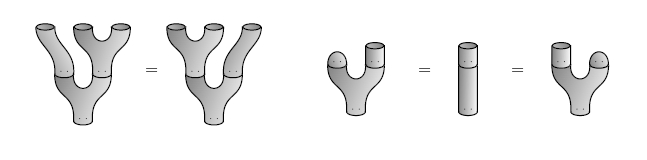
In general there's more to the TQFT than this Frobenius algebra, since there are spacetimes that aren't made of the building blocks I've drawn. But in 2 dimensions, every spacetime can be built from these building blocks: the multiplication and unit, comultiplication and counit. So, with some work, one can show that
This idea goes back to Dijkgraaf:
7) Robbert H. Dijkgraaf, A Geometric Approach To Two-Dimensional Conformal Field Theory, PhD thesis, University of Utrecht, 1989.
and a formal proof was given by Abrams:
8) Lowell Abrams, Two-dimensional topological quantum field theories and Frobenius algebra, Jour. Knot. Theory and its Ramifications 5 (1996), 569-587.
This book is probably the best place to learn the details:
9) Joachim Kock, Frobenius Algebras and 2d Topological Quantum Field Theories, Cambridge U. Press, Cambridge, 2004.
but for a goofier explanation, try this:
10) John Baez, Winter 2001 Quantum Gravity Seminar, Track 1, weeks 11-17, http://math.ucr.edu/home/baez/qg-winter2001/
To prove the equivalence of 2d TQFTs and commutative Frobenius algebras, it's handy to use a different definition of Frobenius algebra, equivalent to the one I gave. I said a Frobenius algebra was an algebra with a nondegenerate bilinear form satisfying
g(ab,c) = g(a,bc).
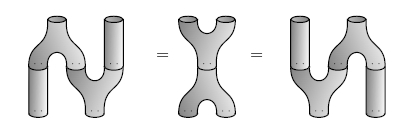
But this is equivalent to having an algebra that's also a coalgebra, with multiplication and comultiplication linked by the "Frobenius equations":
(Δ ⊗ 1A) (1A ⊗ m) = Δ m = (m ⊗ 1A) (1A ⊗ Δ)
These equations are a lot more charismatic in pictures!
We can also interpret them conceptually, as follows. If you have an algebra A, it becomes an (A,A)-bimodule in an obvious way... well, obvious if you know what this jargon means, at least. A ⊗ A also becomes an (A,A)-bimodule, like this:
a (b ⊗ c) d = ab ⊗ cd
Then, a Frobenius algebra is an algebra that's also a coalgebra, where the comultiplication is an (A,A)-bimodule homomorphism! This scary sentence has the Frobenius equations hidden inside it.
The Frobenius equations have a fascinating history, going back to Lawvere, Carboni and Walters, Joyal, and others. Joachim Kock's website includes some nice information about this. Read what Joyal said about Frobenius algebras that made Eilenberg ostentatiously rise and leave the room!
11) Joachim Kock, Remarks on the history of the Frobenius equation, http://mat.uab.es/~kock/TQFT.html#history
The people I just mentioned are famous category theorists. They realized that Frobenius algebra can be generalized from the category of vector spaces to any "monoidal category" - that is, any category with tensor products. And if this monoidal category is "symmetric", it has an isomorphism between X ⊗ Y and Y ⊗ X for any objects X and Y, which lets us generalize the notion of a commutative Frobenius object.
For a nice intro to these ideas, try the slides of this talk:
12) Ross Street, Frobenius algebras and monoidal category, talk at the annual meeting of the Australian Mathematical Society, September 2004, available at http://www.maths.mq.edu.au/~street/FAMC.pdf
These ideas allow for a very slick statement of the slogan I mentioned:
For any n, there's a symmetric monoidal category nCob, with:
The objects are choices of "space", and the morphisms are choices of "spacetime".
The sphere is a very nice object in nCob; let's call it A. Then all the pictures above show that A is a Frobenius algebra in nCob! It's commutative when n > 1. And when n = 2, that's all there is to say! More precisely:
So, to define a 2d TQFT, we just need to pick a commutative Frobenius algebra in Vect (the category of vector spaces). By "freeness", this determines a symmetric monoidal functor
Z: 2Cob → Vect
and that's precisely what a 2d TQFT is!
If you don't know what a symmetric monoidal functor is, don't worry - that's just what I'd secretly been using to translate from pictures of spacetimes to linear operators in my story so far. You can get a precise definition from those seminar notes of mine, or many other places.
Now let's talk about some variations on the slogan above.
We can think of the 2d spacetimes we've been drawing as the worldsheets of "closed strings" - but ignoring the geometry these worldsheets usually have, and keeping only the topology. So, some people call them "topological closed strings".
We can also think about topological open strings, where we replace all our circles by intervals. Just as the circle gave a commutative Frobenius algebra, an interval gives a Frobenius algebra where the multiplication comes from two open strings joining end-to-end to form a single one:
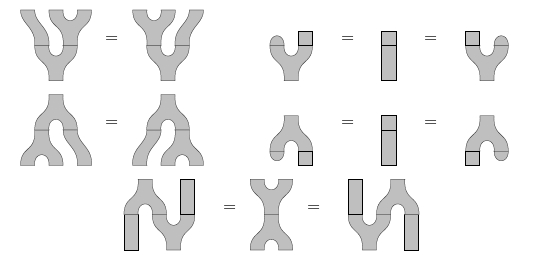
This open string Frobenius algebra is typically noncommutative - draw the picture and see! But, it's still "symmetric", meaning:
g(a,b) = g(b,a)

This is very nice. But physically, open strings like to join together and form closed strings, so it's better to consider closed and open strings together in one big happy family... or category.
The idea of doing this for topological strings was developed by Moore and Segal:
13) Greg Moore, Lectures on branes, K-theory and RR charges, Clay Math Institute Lecture Notes (2002), available at http://www.physics.rutgers.edu/~gmoore/clay1/clay1.html
Lauda and Pfeiffer developed this idea and proved that this category has a nice description in terms of Frobenius algebras:
14) Aaron Lauda and Hendryk Pfeiffer, Open-closed strings: two-dimensional extended TQFTs and Frobenius algebras, Topology Appl. 155 (2008) 623-666. Also available as arxiv:math.AT/0510664.
Here's what they prove, encoded as a mysterious slogan:
If you like the pictures I've been drawing so far, you'll love this paper - since that's where I got most of these pictures! And, it's just the beginning of a longer story where Lauda and Pfeiffer build 2d TQFTs using state sum models:
15) Aaron Lauda and Hendryk Pfeiffer, State sum construction of two-dimensional open-closed topological quantum field theories, J. Knot Theory and its Ramifications 16 (2007), 1121-1163. Also available as arXiv:math/0602047.
This generalizes a construction due to Fukuma, Hosono and Kawai, explained way back in "week16" and also in my seminar notes mentioned above. Then Lauda and Pfeiffer use this machinery to study knot theory!
16) Aaron Lauda and Hendryk Pfeiffer, Open-closed TQFTs extend Khovanov homology from links to tangles, available as math/0606331.
Alas, explaining this would be a vast digression. I want to keep talking about basic Frobenius stuff.
I guess I should say a bit more about semisimple versus non-semisimple Frobenius algebras.
Way back at the beginning of this story, I said you can get a Frobenius algebra by taking the algebra of n × n matrices and defining
g(a,b) = k tr(ab)
for any nonzero constant k. Direct sums of these give all the semisimple Frobenius algebras.
But any algebra acts on itself by left multiplication:
La: b |→ ab
so for any algebra we can try to define
g(a,b) = tr(La Lb)
This bilinear form is nondegenerate precisely when our algebra is "strongly separable":
17) Marcelo Aguiar, A note on strongly separable algebras, available at http://www.math.tamu.edu/~maguiar/strongly.ps.gz
Over the complex numbers, or any field of characteristic zero, an algebra is strongly separable iff it's finite-dimensional and semisimple. The story is trickier over other fields - see that last paper of Lauda and Pfeiffer if you're interested.
Now, for n × n matrices,
g(a,b) = tr(La Lb)
is n times the usual tr(ab). But it's better, in a way. The reason is that for any strongly separable algebra,
g(a,b) = tr(La Lb)
gives a Frobenius algebra with a cute extra property: if we comultiply and then multiply, we get back where we started!
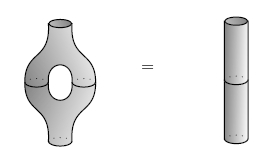
If we use a commutative special Frobenius algebra to get a 2d TQFT, it fails to detect handles! That seems sad. But these papers:
18) Stephen Lack, Composing PROPs, Theory and Applications of Categories 13(2004), 147-163. Available at http://www.tac.mta.ca/tac/volumes/13/9/13-09abs.html
19) R. Rosebrugh, N. Sabadini and R.F.C. Walters, Generic commutative separable algebras and cospans of graphs, Theory and Applications of Categories 15 (Proceedings of CT2004), 164-177. Available at http://www.tac.mta.ca/tac/volumes/15/6/15-06abs.html
makes that sad fact seem good! Namely:
Here Cospan(FinSet) is the category of "cospans" of finite sets. The objects are finite sets, and a morphism from X to Y looks like this:
X Y
\ /
F\ /G
\ /
v v
S
If you remember the "Tale of Groupoidication" starting in
"week247", you'll know about
spans and how to compose spans using pullback. This is just the same
only backwards: we compose cospans using pushout.
But here's the point. A 2d cobordism is itself a kind of cospan:
X Y
\ /
F\ /G
\ /
v v
S
with two collections of circles included in the 2d manifold S. If we
take connected components, we get a cospan of finite sets. Now we've
lost all information about handles! And the circle - which was a
commutative Frobenius algebra - becomes a mere one-point set - which
is a special commutative Frobenius algebra.
Now for a few examples of non-semisimple Frobenius algebras.
First, take the exterior algebra ΛV over an n-dimensional vector space V, and pick any nonzero element of degree n - what geometers would call a "volume form". There's a unique linear map
e: ΛV → C
which sends the volume form to 1 and kills all elements of degree < n. This is a lot like "integration" - and so is taking a trace. So, you should want to make ΛV into a Frobenius algebra using this formula:
g(a,b) = e(a ^ b)
where ^ is the product in the exterior algebra. It's easy to see this is nondegenerate and satisfies the Frobenius axiom:
g(ab,c) = e(a ^ b ^ c) = g(a,bc)
So, it works! But, this algebra is far from semisimple.
If you know about cohomology, you should want to copy this trick replacing the exterior algebra by the deRham cohomology of a compact oriented manifold, and replacing e by "integration". It still works. So, every compact manifold gives us a Frobenius algebra!
If you know about algebraic varieties, you might want to copy this trick replacing the compact manifold by a complex projective variety. I'm no expert on this, but people seem to say that it only works for Calabi-Yau varieties. Then you can do lots of cool stuff:
20) Kevin Costello, Topological conformal field theories and Calabi-Yau categories, available as arxiv:math/0412149.
Here a "Calabi-Yau category" is just the "many-object" version of a Frobenius algebra - a Calabi-Yau category with one object is a Frobenius algebra. There's much more to say about this wonderful paper, but I'm afraid for now you'll have to read it... I'm getting worn out, and I want to get to the new stuff I just learned!
But before I do, I can't resist rounding off one corner I cut. I said that Frobenius algebras show up naturally by taking string theory and watering it down: ignoring the geometrical structure on our string worldsheets and remembering only their topology. A bit more precisely, 2d TQFTs assign linear operators to 2d cobordisms, but conformal field theories assign operators to 2d cobordisms equipped with conformal structures. Can we describe conformal field theories using Frobenius algebras?
Yes!
21) Ingo Runkel, Jens Fjelstad, Jurgen Fuchs, Christoph Schweigert, Topological and conformal field theory as Frobenius algebras, available as arXiv:math/0512076.
But, you need to use Frobenius algebras inside a modular tensor category!
I wish I had more time to study modular tensor categories, and tell you all about them. They are very nice braided monoidal categories that are not symmetric. You can use them to build 3d topological quantum field theories, and they're also connected to other branches of math.
For example, you can modular tensor categories consisting of nice representations of quantum groups. You can also can get them from rational conformal field theories - which is what the above paper by Runkel, Fjelstad, Fuchs and Schweigert is cleverly turning around. You can also get them from von Neumann algebras!
If you want to learn the basics, this book is great - there's a slightly unpolished version free online:
22) B. Bakalov and A. Kirillov, Jr., Lectures on Tensor Categories and Modular Functors, American Mathematical Society, Providence, Rhode Island, 2001. Preliminary version available at http://www.math.sunysb.edu/~kirillov/tensor/tensor.html
But if a book is too much for you, here's a nice quick intro. It doesn't say much about topological or conformal field theory, but it gives a great overview of recent work on the algebraic aspects of tensor categories:
23) Michael Müger, Tensor categories: a selective guided tour, available as arXiv:0804.3587.
Here's a quite different introduction to recent developments, at least up to 2004:
24) Damien Calaque and Pavel Etingof, Lectures on tensor categories, available as arXiv:math/0401246.
Still more recently, Hendryk Pfeiffer has written what promises to be a fundamental paper describing how to think of any modular tensor category as the category of representations of an algebraic gadget - a "weak Hopf algebra":
25) Hendryk Pfeiffer, Tannaka-Krein reconstruction and a characterization of modular tensor categories, available as arXiv:0711.1402.
And here's a paper that illustrates the wealth of examples:
26) Seung-moon Hong, Eric Rowell, Zhenghan Wang, On exotic modular tensor categories, available as arXiv:07108.5761.
The abstract of this makes me realize that people have bigger hopes of understanding all modular tensor categories than I'd imagined:
It has been conjectured that every (2+1)-dimensional TQFT is a Chern-Simons-Witten (CSW) theory labelled by a pair (G,k), where G is a compact Lie group, and k in H4(BG,Z) is a cohomology class. We study two TQFTs constructed from Jones' subfactor theory which are believed to be counterexamples to this conjecture: one is the quantum double of the even sectors of the E6 subfactor, and the other is the quantum double of the even sectors of the Haagerup subfactor. We cannot prove mathematically that the two TQFTs are indeed counterexamples because CSW TQFTs, while physically defined, are not yet mathematically constructed for every pair (G,k). The cases that are constructed mathematically include:
- G is a finite group - the Dijkgraaf-Witten TQFTs;
- G is a torus Tn;
- G is a connected semisimple Lie group - the Reshetikhin-Turaev TQFTs.
We prove that the two TQFTs are not among those mathematically constructed TQFTs or their direct products. Both TQFTs are of the Turaev-Viro type: quantum doubles of spherical tensor categories. We further prove that neither TQFT is a quantum double of a braided fusion category, and give evidence that neither is an orbifold or coset of TQFTs above. Moreover, the representation of the braid groups from the half E6 TQFT can be used to build universal topological quantum computers, and the same is expected for the Haagerup case.
Anyway, now let me say what Vicary and Melliès have been explaining to me. I'll give it in a highly simplified form... and all mistakes are my own.
First, from what I've said already, every commutative special Frobenius algebra over the complex numbers looks like
C ⊕ C ⊕ ... C ⊕ C
It's a direct sum of finitely many copies of C, equipped with its god-given bilinear form
g(a,b) = tr(La Lb)
So, this sort of Frobenius algebra is just an algebra of complex functions on a finite set. A map between finite sets gives an algebra homomorphism going back the other way. And the algebra homomorphisms between two Frobenius algebras of this sort all come from maps between finite sets.
So, the category with:
is equivalent to FinSetop. This means we can find the category of finite sets - or at least its opposite, which is just as good - lurking inside the world of Frobenius algebras!
Coecke, Pavlovic and Vicary explore the ramifications of this result for quantum mechanics, using Frobenius algebras that are Hilbert spaces instead of mere vector spaces. This lets them define a "†-Frobenius algebra" to be one where the comultiplication and counit are adjoint to the the multiplication and unit. They show that making a finite-dimensional Hilbert space into a commutative special †-Frobenius algebra is the same as equipping it with an orthonormal basis.
There's no general way to duplicate quantum states - "you can't clone a quantum" - but if you only want to duplicate states lying in a chosen orthonormal basis you can do it. So, you can think of commutative special †-Frobenius algebras as "classical data types", which let you duplicate information. That's what the comultiplication does: duplicate!

Any commutative special †-Frobenius algebra has a finite set attached to it: namely, the set of basis elements. So, we now see how to describe finite sets starting from Hilbert spaces and introducing a notion of "classical data type" formulated purely in terms of quantum concepts.
The papers by Coecke, Pavlovic and Vicary go a lot further than my summary here. Jamie Vicary even studies how to categorify everything I've just mentioned!
A subtlety: it's a fun puzzle to show that in any monoidal category, morphisms between Frobenius algebras that preserve all the Frobenius structure are automatically isomorphisms. See the slides of Street's talk if you get stuck: he shows how to construct the inverse, but you still get the fun of proving it works.
So, the category with:
is equivalent to the groupoid of finite sets. We get FinSetop if we take algebra homomorphisms, and I guess we get FinSet if we take coalgebra homomorphisms.
Finally, a bit about categorified Frobenius algebras and logic!
I'm getting a bit tired, so I hope you believe that the concept of Frobenius algebra can be categorified. As I already mentioned, Frobenius algebras make sense in any monoidal category - and then they're sometimes called "Frobenius monoids". Similarly, categorified Frobenius algebras make sense in any monoidal bicategory, and then they're sometimes called "Frobenius pseudomonoids". These were introduced in Street's paper "Frobenius monads and pseudomonoids", cited above - but if you like pictures, you may also enjoy learning about them here:
27) Aaron Lauda, Frobenius algebras and ambidextrous adjunctions,
Theory and Applications of Categories 16 (2006), 84-122, available at
http://tac.mta.ca/tac/volumes/16/4/16-04abs.html
Also available as arXiv:math/0502550.
I explained some of the basics behind this paper in "week174".
But now, I want to give a definition of *-autonomous categories, which simultaneously makes it clear that they're natural structures in logic, and that they're categorified Frobenius algebras!
Suppose A is any category. We'll call its objects "propositions" and its morphisms "proofs". So, a morphism
f: a → b
is a proof that a implies b.
Next, suppose A is a symmetric monoidal category and call the tensor product "or". So, for example, given proofs
f: a → b, f': a' → b'
we get a proof
f or f': a or a' → b or b'
Next, suppose we make the opposite category Aop into a symmetric monoidal category, but with a completely different tensor product, that we'll call "and". And suppose we have a monoidal functor:
not: A → Aop
So, for example, we have
not(a or b) = not(a) and not(b)
or at least they're isomorphic, so there are proofs going both ways.
Now we can apply "op" and get another functor I'll also call "not":
not: Aop → A
Using the same name for this new functor could be confusing, but it shouldn't be. It does the same thing to objects and morphisms; we're just thinking about the morphisms as going backwards.
Next, let's demand that this new functor be monoidal! This too is quite reasonable; for example it implies that
not(a and b) = not(a) or not(b)
or at least they're isomorphic.
Next, let's demand that this pair of functors:
not
--------->
A Aop
<----------
not
be a monoidal adjoint equivalence. So, for example, there's a
one-to-one correspondence between proofs
not(a) → b
and proofs
not(b) → a
Now for the really fun part. Let's define a kind of "bilinear form":
g: A × A → Set
where g(a,b) is the set of proofs
not(a) → b
And let's demand that g satisfy the Frobenius axiom! In other words, let's suppose there's a natural isomorphism:
g(a or b, c) ≅ g(a, b or c)
Then A is a "*-autonomous category"! And this is a sensible notion, since it amounts to requiring a natural one-to-one correspondence between proofs
not(a or b) → c
and proofs
not(a) → b or c
So, categorified Frobenius algebras are a nice framework for propositional logic!
In case it slipped by too fast, let me repeat the definition of *-autonomous category I just gave. It's a symmetric monoidal category A with a monoidal adjoint equivalence called "not" from A (with one tensor product, called "or") to Aop (with another, called "and"), such that the functor
g: A × A → Set (a,b) |→ hom(not(a),b)is equipped with a natural isomorphism
g(a or b, c) ≅ g(a, b or c)
I hope I didn't screw up. I want this definition to be equivalent to the usual one, which was invented by Michael Barr quite a while ago:
28) Michael Barr, *-Autonomous Categories, Lecture Notes in Mathematics 752, Springer, Berlin, 1979.
By now *-autonomous categories become quite popular among those working at the interface of category theory and logic. And, there are many ways to define them. Brady and Trimble found a nice one:
29) Gerry Brady and Todd Trimble, A categorical interpretation of C. S. Peirce's System Alpha, Jour. Pure Appl. Alg. 149 (2000), 213-239.
Namely, they show a *-autonomous category is the same as a symmetric monoidal category A equipped with a contravariant adjoint equivalence
not: A → A
which is equipped with a "strength", and where the unit and counit of the adjunction respect this strength.
Later, in his paper "Frobenius monads and pseudomonoids", Street showed that *-autonomous categories really do give Frobenius pseudomonoids in a certain monoidal bicategory with:
Alas, I'm too tired to explain this now! It's a slicker way of saying what I already said. But the cool part is that this bicategory is like a categorified version of Vect, with the category of finite sets replacing the complex numbers. That's why in logic, the "nondegenerate bilinear form" looks like
g: A × A → Set
So: Frobenius algebras are lurking all over in physics, logic and quantum logic, in many tightly interconnected ways. There should be some unified explanation of what's going on! Do you have any ideas?
Finally, here are two books on math and music that I should read someday. The first seems more elementary, the second more advanced:
30) Trudi Hammel Garland and Charity Vaughan Kahn, Math and Music - Harmonious Connections, Dale Seymour Publications, 1995. Review by Elodie Lauten on her blog Music Underground, http://www.sequenza21.com/2007/04/microtonal-math-heads.html
31) Serge Donval, Histoire de l'Acoustique Musicale (History of Musical Acoustics), Editions Fuzaeau, Bressuire, France, 2006. Review at Music Theory Online, http://mto.societymusictheory.org/mto-books.html?id=11
Addenda: I thank Bob Coecke, Robin Houston, Steve Lack, Paul-André Melliès, Todd Trimble, Jamie Vicary, and a mysterious fellow named Stuart for some very helpful corrections.
You can't really appreciate the pictorial approach to Frobenius algebras until you use it to prove some things. Try proving that every homomorphism of Frobenius algebras is an isomorphism! Or for something easier, but still fun, start by assuming that a Frobenius algebra is an algebra and coalgebra satisfying the Frobenius equations


For more discussion, visit the n-Category Café. In particular, you'll see there's a real morass of conflicting terminology concerning what I'm calling "special" Frobenius algebras and "strongly separable" algebras. But if we define them as I do above, they're very nicely related.
More precisely: an algebra is strongly separable iff it can be given a comultiplication and counit making it into a special Frobenius algebra. If we can do this, we can do it in a unique way. Conversely, the underlying algebra of a special Frobenius algebra is strongly separable.
For more details, see:
32) nLab, Frobenius algebra, http://ncatlab.org/nlab/show/Frobenius+algebra
and:
33) nLab, Separable algebra, http://ncatlab.org/nlab/show/separable+algebra
'Interesting Truths' referred to a kind of theorem which captured subtle unifying insights between broad classes of mathematical structures. In between strict isomorphism - where the same structure recurred exactly in different guises - and the loosest of poetic analogies, Interesting Truths gathered together a panoply of apparently disparate systems by showing them all to be reflections of each other, albeit in a suitably warped mirror. - Greg Egan, Incandescence
© 2008 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|