




|
 
|

|
I'm very happy to have finished writing a huge paper with Aaron Lauda... a paper we've been working on for 5 years! It's a chronology of 20th century math and physics, focused on why people are starting to use n-categories in physics:
1) John Baez and Aaron Lauda, A prehistory of n-categorical physics, to appear in Deep Beauty: Mathematical Innovation and the Search for an Underlying Intelligibility of the Quantum World, edited by Hans Halvorson. Available at http://math.ucr.edu/home/baez/history.pdf
This is a companion to a paper I talked about in "week261":
2) John Baez and Mike Stay, Physics, topology, logic and computation: a Rosetta Stone, to appear in New Structures in Physics, edited by Bob Coecke. Available as arXiv:0903.0340.
Both of them are supposed to be gentle explanations of how "diagrammatic thinking" unifies and clarifies our perspective on many subjects. I can imagine merging them and expanding them to form a book someday... but not today. Today I want to take a break from n-categories, and talk about some basic physics.
Let's start with a riddle.
What's a million times thinner than paper, stronger than diamond, a better conductor than copper, and absorbs exactly
π α ~ 3.14159 / 137.035 ~ 2.29254%
of the light you shine through it?
Hint: α is the "fine structure constant" - a fundamental dimensionless constant that specifies the strength of the electromagnetic force.
Can't guess? Okay, here's the answer: graphene!

Graphene is what you get when you take one slice of a crystal of graphite. It's a hexagonal array of carbon atoms, each connected to three neighbors. I mentioned this substance back in "week262", when I was visiting the National University of Singapore, because researchers there were working on graphene as a possible substitute for silicon chips, which might operate 1000 times faster. Now a group there led by Barbaros Özyilmaz is trying to use graphene for storing information:
3) Prachi Patel, A step towards superfast carbon memory, Technology Review, Wednesday April 1, 2009, available at http://www.technologyreview.com/computing/22377/.
No, this is not an April Fool's joke.
Graphene was only discovered in 2004, but the easiest way to make some is surprisingly lowtech. You press a chunk of graphite onto some scotch tape, and hope a thin layer sticks:
4) Making graphene 101, Özyilmaz' group, YouTube video, available at http://www.youtube.com/watch?v=rphiCdR68TE
Graphene has some amazing properties. For starters, it acts like a toy universe containing massless spin-1/2 particles, which zip around at the speed of light. But in this toy universe, light moves 300 times slower than in the real universe!
To understand this, you have to start by realizing that any sort of wave also acts like a particle when you take quantum mechanics into account. The idea is that when something can wiggle back and forth at some frequency, it can wiggle a little or a lot - but it can't wiggle just any amount. The amount of wiggling is "quantized" - it comes in discrete steps. These steps are too small to see in normal life, where for example you might see a rubber band seem to vibrate with any amplitude it wants. But these quantized steps are there nonetheless, no matter what is doing the wiggling - it appears to be a completely general principle.
When the wiggles are waves that are moving along, these quantized steps are called "particles". So, for example, when we have a wave of light of some particular frequency that contains 500 times more energy than the bare minimum, we say it consists of 500 "particles" called photons. At first this may sound weird, but it turns out that many things we normally consider particles - like electrons and protons and neutrons - really are just quantized wiggles of some sort or another.
In cases like these, the stuff that's doing the wiggling is rather absract: for photons, we say it's the "electromagnetic field", and for other particles we say it's various other fields.
But since the principle is completely general, there are also cases where the stuff doing the wiggling is quite mundane. For example, if you have a crystal, the crystal's atoms can wiggle. This is of course how sound propagates. But this should mean that sound comes in quantized packets called "phonons". And indeed, experiments with crystals show that this is true!
5) Wikipedia, Phonon, http://en.wikipedia.org/wiki/Phonon
Different vibrational modes of the crystal have different numbers of wiggles per distance, and different numbers of wiggles per time; these give phonons with different momentum and energy. The relation is simple:
momentum = h (wiggles per distance)
energy = h (wiggles per time)
where h is Planck's constant, a tiny little constant.
(Why am I talking about sound in crystals, rather than air? It's because our story applies in its simplest form to vibrational modes that don't interact much with other modes or get damped out quickly by friction. These give rise to particles that don't interact much with other particles, and don't decay very fast - so they're easy to see.)
There are other things about a crystal that can vibrate besides the atoms. For example, the atoms may have an angular momentum, or "spin", that can change directions. Often each atom's spin affects its neighbors through magnetic forces. This allows waves of changed spin - "spin waves" - to propagate through the crystal. And again, these waves come in quantized packets called "magnons":
6) Wikipedia, Spin wave, http://en.wikipedia.org/wiki/Spin_wave
A crystal can also have a "hole": an atom with a missing electron These holes can move around, so they too act like particles. This example is perhaps a bit more obvious than the previous ones... so here I should probably emphasize that just as sound waves or spin waves come in discrete particle-like units, these holes act like waves!
Similarly, a crystal can have atom with an extra electron. Here it's even more obvious that these electrons act like particles - you probably want to just say they are particles. But at this point it's crucial to emphasize that this example is really like all the rest. In particular (pardon the pun), we need to understand these extra electrons in terms of waves, and we need to compute their energy and momentum using these formulas:
momentum = h (wiggles per distance)
energy = h (wiggles per time)
so the relation between the energy and momentum depends completely on the details of the crystal: you can't just use some formula you may happen to know about a "free" electron in empty space. So, electrons in crystals can do all sorts of crazy things that you'd never expect, and indeed this is what makes things like conductors and transistors possible.
Let's talk about relations between energy and momentum. For a particle of mass m in empty space, special relativity says that
energy2 = momentum2 + mass2
in units where the speed of light is 1. If we work in units where the speed of light is some number c, the formula looks messier:
energy2 = momentum2 c2 + mass2 c4
If you look at a particle at rest, its momentum is zero so a little calculation reveals that:
energy = mass c2
which is a pretty famous formula.
But if we go to the other extreme, and look at "massless" particle, meaning one with mass = 0, we get
energy = momentum c
which is also famous, but less so. If we apply the formulas
momentum = h (wiggles per distance)
energy = h (wiggles per time)
we get
wiggles per time = c (wiggles per distance)
This fact is easy to believe if we imagine light as a wave moving along, and c as the speed of this wave. Indeed, this fact was important in helping guess the relation between momentum and "wiggles per distance", and energy and "wiggles per time", back when they were first inventing quantum mechanics.
Now, the above formulas apply to photons in empty space. But my real point is this: if we have any sort of substance and any sort of wave that can move around in this substance, obeying these formulas, it acts like a massless particle. So, we can use a lot of the same math and intuition that we use for photons. But, quite likely the value of c will be different than the real-world speed of light!
And this in fact is what happens for graphene. The calculation is pathetically simple by ordinary physics standards, yet complicated enough that I don't feel like presenting the details here. You can see it near the beginning of this wonderful paper:
7) Jiannis K. Pachos, Manifestations of topological effects in graphene, to appear in Contemp. Phys.. Also available as arXiv:0812.1116.
You start with a really simplified model: a planar hexagonal honeycomb that can either have or lack an electron at each vertex. You ignore the spin of the electron for some reason. It's a bit surprising you can get away with that! You assume the energy is a bit less whenever you've got electrons at both ends of any given edge of your hexagonal honeycomb.
It helps to color the vertices of the honeycomb alternately black and white. Then there are two kinds of electrons: "black" and "white" ones. The formula for the energy can be expressed nicely in terms of these, because it's a sum over pairs of neighboring vertices, one black and one white. Note that whenever an electron moves, it changes from black to white or vice versa.
Then you do a little calculating: you do a Fourier transform here, you diagonalize a 2×2 matrix there, and... presto!
There turn out to be two different kinds of waves, each consisting of a certain linear combination of black and white electrons. The energy of these waves (or if you prefer, their number of wiggles per time) is related to their momentum (or wiggles per distance) by a complicated formula.
To write down this formula, we have to treat momentum as a vector, since the energy of a wave depends on which direction it's going: the hexagonal honeycomb means that not all direction behave the same. If you plot the energy E as a function of the momentum vector p = (px,py), you get a graph like this:
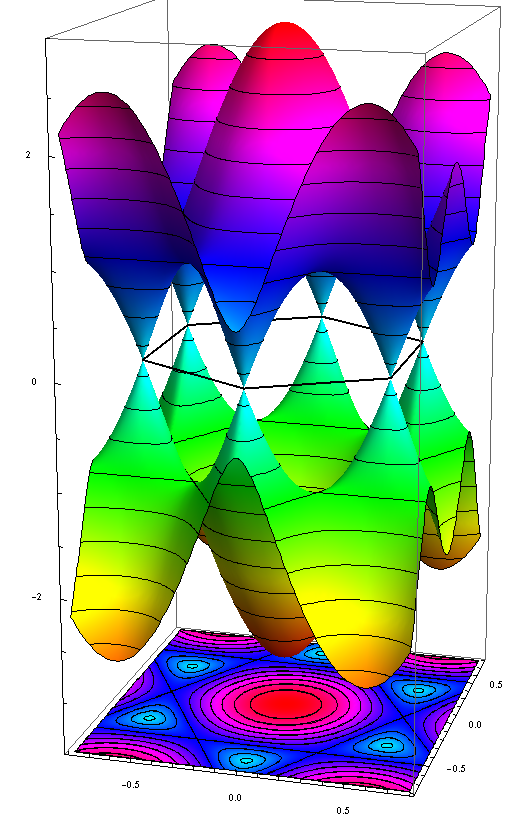
It's pretty fancy! But you can see it has hexagonal symmetry, as you'd expect. And it's also periodic. This comes from the periodicity of the crystal lattice - but in sneaky way: the crystal lattice in actual space gives rise to a "dual lattice" in the space of momentum vectors, and the energy stays the same if you take the momentum and add any vector in this dual lattice. This is no big deal, it happens for any crystal:
8) Wikipedia, Reciprocal lattice, http://en.wikipedia.org/wiki/Reciprocal_lattice
In crystal jargon, the original crystal lattice is called the "Bravais lattice" and its dual is called the "reciprocal lattice".
The big deal is that if you look carefully at certain points in the graph, it looks almost like a cone.
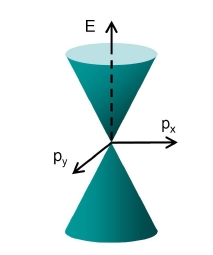
E2 = (px2 + py2) c2
or in other words:
energy2 = momentum2 c2
for some constant c. And this is just the relation we had for a massless particle!
A digression: when I wrote this relation before, I took a square root and got
energy = momentum c
But the above graph includes negative energies as well. What do the negative energies mean, physically? That's an interesting puzzle, which people had to confront when they were first trying to combine special relativity and quantum mechanics. I don't want to talk about it here, but if you're curious, see this:
9) M. I. Katnelson, K. S. Novoselov, A. K. Geim, Chiral tunnelling and the Klein paradox in graphene, Nature Physics 2 (2006), 620.
Anyway, the upshot is that near one of these special points, graphene acts like it has two kinds of massless particles in it: "black" and "white". They are approximately described by the usual equation for massless spin-1/2 particles, the Dirac equation - but in a universe with just 2 dimensions of space! The speed c is about 1/300th of the real-world speed of light. Also, a spin-1/2 particle in 2d space usually comes in two states: it can rotate clockwise or counterclockwise. But here those two states are certain linear combinations of "black" and "white".
Furthermore, because the formula
energy2 = momentum2 c2
remains unchanged when you rescale both distances and times by the same factor, graphene reacts exactly the same way to light of different wavelengths - at least within some range where all the approximations we've made are good. And, it turns out to absorb πα of the light you shine through it:
10) A. B. Kuzmenko, E. van Heumen, F. Carbone, and D. van der Marel, Universal infrared conductance of graphite, Phys. Rev. Lett. 100 (2008), 117401.
11) R. R. Nair, P. Blake, A. N. Grigorenko, K. S. Novoselov, T. J. Booth, T. Stauber, N. M. R. Peres, and A. K. Geim, A. K., Fine structure constant defines visual transparency of graphene, Science 320 (2008), 1308. Also available at http://onnes.ph.man.ac.uk/nano/Publications/Science_2008fsc.pdf
So, graphene is an amazing physical system, but so far I've just scratched the surface. Graphene also has "topological defects", and "anyons", and there are wonderful applications of Euler's theorem and its big brother, the Atiyah-Singer index theorem. All this in a physical system you can make by pressing graphite against a piece of tape!
I should say more about all this, but I need to go to bed and then catch an early morning plane. So, I'll quit here - but I highly recomend Pachos' paper "Manifestations of topological effects in graphene".
Addenda: For more discussion visit the n-Category Café.
Error and doubt no longer encumber us with mist;
We are now admitted to the banquets of the Gods;
We may deal with laws of heaven above; and we now have
The secret keys to unlock the obscure earth. - Halley
© 2009 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|