




|
 
|

|
I just finished a paper with John Huerta, a math grad student who really likes particle physics:
1) John Baez and John Huerta, Division algebras and supersymmetry, available as arXiv:0909.0551.
You can think of this paper as our sequel to:
2) John Baez, OP1 and Lorentzian geometry, http://math.ucr.edu/home/baez/octonions/node11.html
A "normed division algebra" is an algebraic gadget where you can add, multiply, subtract, and divide, satisfying all the usual laws except the commutative and associative laws for multiplication, and where every element has an "absolute value" or "norm" satisfying the usual rules, including most notably:
|xy| = |x| |y|
The most popular example is the real numbers. The second most popular example is the complex numbers. Then comes the quaternions, which are noncommutative... and then, trailing in a distant fourth place, comes the octonions, which are noncommutative and nonassociative.
Our paper aims to give a clear and self-contained treatment of the amazing relation between normed division algebras and supersymmetric Yang-Mills theory. Let me explain the basic idea! I'll cut some corners, but you can see all the details in our paper.
Suppose K is a normed division algebra of dimension n. There are just four choices:
We get all of these by taking the real numbers and throwing in square roots of minus 1. So, any guy in K has a "real part" and an "imaginary part" - and we can "conjugate" it by switching the sign of its imaginary part.
This means we can talk about hermitian matrices with entries in K: that is, matrices that stay the same when you transpose them and then conjugate each entry. Let's use h2(K) to mean the set of hermitian 2×2 matrices with entries in K.
Then a nice thing happens: h2(K) is the same as (n+2)-dimensional Minkowski spacetime! To see this, note that any guy in h2(K) has this form:
A = t+x y
y* t-x
where t and x are real elements of K, and y is an arbitrary element.
Since K has dimension n, h2(K) has dimension n+2. And check out
its determinant:
det(A) = t2 - x2 - yy*
Note that yy* = y*y = |y|2, just as in the complex numbers. So, det(A) is a Minkowski metric with one positive or "timelike" direction, namely t, and n+1 negative or "spacelike" directions, namely x and the n components of y.
So:
And - lo and behold! - these are just the dimensions where classical superstring theory and super-Yang-Mills theory work best!
More precisely, these are the dimensions where you can write down the Lagrangian for the "Green-Schwarz superstring" and "pure super-Yang-Mills theory". There are fancier tricks that give superstring theories and super-Yang-Mills theories in other dimensions, but these are mainly offshoots of the four cases listed here.
So now we have to ask: why do these supersymmetric theories feel so happy when spacetime is secretly h2(K)?
Well, supersymmetry is a kind of symmetry that mixes bosons and fermions. In the simple cases I'm talking about, this means mixing vectors and spinors. Since vectors are the same as points in Minkowski spacetime - once we pick an origin - vectors in dimensions 3, 4, 6, or 10 are nicely described by elements of h2(K). And it turns out that supersymmetry works well in these dimensions because we can also describe spinors using K. A spinor consists of 2 guys in K: in other words, an element of K2.
Indeed, if you've studied physics, you may know that in 4d Minkowski spacetime, where we apparently live, we use C2 to describe spinors. I talked quite a bit about this example and also the example of 3d Minkowski spacetime back in "week196". So go there if you want more details. For now what matters is this:
This is a bit oversimplified, because physicists use various kinds of spinors, and I'm not saying which kinds show up here. But I explained all these kinds back in "week93", and I don't want to distract you with that here. I'll say more about it later.
Now, from what we've seen so far, there's an obvious way to take a vector and a spinor and get a new spinor. This is what matrices were born for! Just take your matrix in h2(K), multiply your spinor in K2 by that matrix, and you get a new spinor in K2.
In fact, we see this process at work whenever an electron absorbs a photon. Quite literally, we see it - because that's how our eyes work! A photon is described by a vector, an electron is described by a spinor, and part of the math involved when an electron absorbs a photon is this business of matrix multiplication.
Physicists would draw this operation using a Feynman diagram where a wiggly line (the vector) and a straight one (the spinor) come in and a straight one goes out:
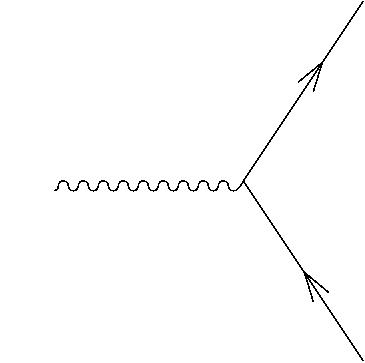
Mathematicians would write it as the operation that takes A in h2(K) and ψ in K2 and multiplies them to get Aψ in h2(K).
Now, one cool thing about Feynman diagrams is that you can turn them around and read them in different ways, and they still make sense. So as soon as we have a process where a spinor absorbs a vector, we also get a process where two spinors collide and form a vector:

So, we've got an operation that takes a vector and a spinor and creates a spinor, and an operation that takes two spinors and creates a vector. Actually, these operations exist for any dimension of spacetime! In general we need to describe them using the language of Clifford algebras. Only in dimensions 3, 4, 6 and 10 can we describe them using the language of normed division algebras, as I've done here.
But it's this special language that gives the prettiest explanation of a certain astounding fact. Supersymmetry for the Green-Schwarz superstring and pure super-Yang-Mills theory relies on a special identity which is true only in dimensions 3, 4, 6 and 10:
(ψ·ψ) ψ = 0
This is an example of a "Fierz identity". These equations show up whenever you work with spinors, and they should probably be called "fierce identities", because they can be pretty scary. In particular, it's a bit scary how some of them - like this one - hold only in certain special dimensions.
But this particular one has a beautiful proof in terms of normed division algebras! It follows from a special property shared by these algebras: they're all "alternative". In other words, the "associator"
[x,y,z] = (xy)z - x(yz)
changes sign whenever we switch any of the two variables. The associator is just zero for R, C, and H, since these algebras are associative. So the only really interesting case is the octonions, which are not associative, but still alternative. And this is the case that matters for superstring theory in 10 dimensions!
Anyway, what our paper does is describe the basic operations involving spinors and vectors using the normed division algebras, then use this description to prove the identity
(ψ·ψ) ψ = 0,
and then explain how this identity is crucial in supersymmetric Yang-Mills theory. None of this is particularly new! What's new, we hope, is that we explain everything in one place, in a way that people who don't know about division algebras or supersymmetry can follow. Some of the proofs use a little Clifford algebra technology, but most of them amount to simple calculations.
Now let me tell you a tiny bit about the history of this subject, with references. I would love to hear more details from people who were around at the time. As far as I can tell, this is the first paper that explained super-Yang-Mills theory and why it only works in dimensions 3, 4, 6 and 10:
3) Lars Brink, John Schwarz and Joel Scherk, Supersymmetric Yang-Mills theory, Nucl. Phys. B 121 (1977), 77-92.
Well, actually 2, 4, 6, and 10, but never mind! This is the paper that did it for superstring theory:
4) Michael Green and John Schwarz, Covariant description of superstrings, Phys. Lett. B136 (1984), 367-370.
The bible of string theory contains proofs of these facts, based on the properties of Clifford algebras in various dimensions:
5) Michael B. Green, John H. Schwarz and Edward Witten, Superstring Theory, Volume 1, Cambridge U. Press, Cambridge, 1987. Appendix 4.A, Super Yang-Mills Theory, pages 244-247. Section 5.1.2: The supersymmetric string action, pp. 253-255.
Back in 1983, Kugo and Townsend showed how spinors in dimension 3, 4, 6, and 10 get special properties from the normed division algebras. They formulated a supersymmetric model in 6 dimensions using the quaternions, and speculated about a similar formalism in 10 dimensions using the octonions:
6) Taichiro Kugo and Paul Townsend, Supersymmetry and the division algebras, Nucl. Phys. B 221 (1983), 357-380. Also available at http://ccdb4fs.kek.jp/cgi-bin/img_index?198301032
Later, Evans showed that supersymmetry of nonabelian Yang-Mills fields coupled to massless spinors in (n+2)-dimensional spacetime implies the existence of a normed division algebra of dimension n:
7) J. M. Evans, Supersymmetric Yang-Mills theories and division algebras, Nucl. Phys. B 298 (1988), 92-108. Also available at http://ccdb4fs.kek.jp/cgi-bin/img_index?8801412
Shortly after Kugo and Townsend's work, Tony Sudbery used division algebras to construct vectors, spinors and Lorentz groups in Minkowski spacetimes of dimensions 3, 4, 6, and 10:
8) Anthony Sudbery, Division algebras, (pseudo)orthogonal groups and spinors, Jour. Phys. A17 (1984), 939-955.
He then refined his construction with the help of a grad student:
9) Kwok-Wai Chung and Anthony Sudbery, Octonions and the Lorentz and conformal groups of ten-dimensional space-time, Phys. Lett. B198 (1987), 161-164.
Tony Sudbery and Corinne Manogue then used these ideas to give an octonionic proof that (ψ . ψ) ψ = 0.
10) Corinne Manogue and Anthony Sudbery, General solutions of covariant superstring equations of motion, Phys. Rev. D12 (1989), 4073-4077.
Together with her husband and Jason Janesky, Manogue later simplified the proof, and our argument is based on theirs:
11) Tevian Dray, Jason Janesky and Corinne Manogue, Octonionic hermitian matrices with non-real eigenvalues, Adv. Appl. Clifford Algebras 10 (2000), 193-216. Appendix B, The 3-Ψ's rule. Also available as arXiv:math/0006069.
They give a little more history of this wondrous identity. They say that Manogue's student Schray called it "the 3-Ψ's rule" in his hard-to-obtain thesis:
12) Jörg Schray, Octonions and supersymmetry, Ph.D. thesis, Department of Physics, Oregon State University, 1994.
and also here:
13) Jörg Schray, The general classical solution of the superparticle, Class. Quant. Grav. 13 (1996), 27-38. Also available as arXiv:hep-th/9407045.
They also write:
It is well-known that the 3-Ψ's rule holds for Majorana spinors in 3 dimensions, Majorana or Weyl spinors in 4 dimensions, Weyl spinors in 6 dimensions and Majorana-Weyl spinors in 10 dimensions. Thus, the Green-Schwarz superstring exists only in those cases. As was shown by Fairlie and Manogue, the 3-Ψ's rule in all these cases is equivalent to an identity on the gamma-matrices, which holds automatically for the natural representation of the gamma-matrices in terms of the 4 division algebras R, C, H and O, corresponding precisely to the above 4 types of spinors. Manogue and Sudbery then showed how to rewrite these spinor expressions in terms of 2x2 matrices over the appropriate division algebra, thus eliminating the gamma-matrices completely.Now I feel like explaining all this Majorana/Weyl business a bit better - leaving many details to "week93".
First I should admit, for the nonexperts, that I've committed a few sins of oversimplification for the sake of a nice clean story line. For starters, remember how I said that the absorption of a photon by an electron:

In saying this, I was ignoring everything about energy and momentum, and focusing on the "spin" aspect of this absorption process. It's only the "spin", or intrinsic angular momentum, of a photon that's described by an element of h2(K) - with K = C, since we live in 4-dimensional spacetime. And it's only the spin of the electron that's described by an element of K2.
But it's even worse than that. In 4-dimensional spacetime, spinors come in left- and right-handed forms. For example, the neutrinos we most easily see - not that easily, actually! - are left-handed spinors, while antineutrinos are right-handed. Electrons come in both left and right-handed forms, so we actually describe them using C2 ⊕ C2 = C4. We call C4 the space of "Dirac spinors", and we call the two pieces left- and right-handed "Weyl spinors".
Similar but subtly different things happen in other dimensions. As far as our division algebras story goes, the crucial fact is that besides the "obvious" way for an element of h2(K) to act on K2, there is a less obvious way that involves the "traced-reversed" form of a 2×2 hermitian matrix:
A~ = A - tr(A)
where the trace tr(A) is the sum of the diagonal entries. We get one kind of spinors, say
S+ = K2
upon which the vectors
V = h2(K)
act in the obvious way, and another kind of spinors, say
S- = K2
in which vectors act in a nonobvious way. As vector spaces S+ and S- are the same - but they differ in how vectors act on them, and we should think of this action as interchanging the two kinds of spinor. Here are the formulas:
V ⊗ S+ → S-
A ⊗ ψ |→ Aψ
V ⊗ S- → S+
A ⊗ ψ |→ A~ ψ
These actions fit together to yield a Clifford algebra action on the direct sum of S+ and S-, since
A A~ = A~ A = -det(A)
and the determinant is related to the metric on Minkowski spacetime, so these are the Clifford algebra relations in deep disguise.
What all this really amounts to depends a lot on which of the four division algebras we're looking at! Sometimes S+ and S- are secretly isomorphic, sometimes not. They always start out being real vector spaces, since as vector spaces they're just K2, and the only uniform way to think of all four normed division algebras is as real vector spaces. But sometimes S+ and S- admit Lorentz-invariant complex structures, so we can think of them as complex vector spaces!
(By "Lorentz-invariant" I really mean invariant under the action of the double cover of the Lorentz group. For brevity, let's just call this the Lorentz group.)
In fact, each of the four cases has its own unique personality, with the 4d case being the weirdest - you might call it a "split personality". Let me just summarize the facts, without much explanation. This is one of those things where I write stuff down so I can forget it and look it up later:
But in fact this real vector space has two invariant complex structures, and the resulting complex representations are not isomorphic! If we think of S+ and S- as two nonisomorphic complex representations we call their elements left- and right-handed "Weyl" spinors, respectively - since that's the name for complex spinors that do have a particular handedness.
Wow, I bet that was thrilling!
Now that I'm done with this paper, my life has undergone a phase change. I've been finishing a lot of old papers for the last 2 years. This is the last of that batch - and the least old. It comes as an incredible relief. Working on old projects is tiring, especially when you have new things you're dying to think about. I feel like I've been way behind myself, running to catch up... but this week I finally caught up and ran past myself! It's a strange sensation.
Adding to this strange sensation, I just got word that I'm free to take leave from UCR and visit Singapore for a year, starting in July 2010. I'll be working at the Centre for Quantum Technologies. That should be a great adventure.
So, I'm feeling peppy, and I'm dying to tell you about all sorts of new cool stuff: Stirling numbers and the Poisson operad, stacks and noncommutative geometry, Adams operations and Galois theory, toric varieties, octonions and rolling balls, the windmill powered by light, and the symplectic geometry of electrical circuits. Each of these deserves a whole Week, but we'll see.
For now, here are a few cool things I won't tell you much about, because I don't understand them well enough. First, as pointed out to me by Mike Stay:
14) Generalized continued fractions and equal temperament, Doctroidal Dissertations, April 13th, 2009, http://doctroid.wordpress.com/2009/04/13/
This starts with the old problem of trying to find a number x such that xn = 2 and xk is almost 3/2. In music jargon, this is called "finding an equal tempered scale that has a good fifth". In math jargon, it amounts to finding a good rational approximation to
log(3/2)/log(2) ~ 0.584962501
The theory of continued fractions gives us candidates:
0/1 = 0.000000 1/1 = 1.000000 1/2 = 0.500000 3/5 = 0.600000 7/12 = 0.583333 24/41 = 0.585366 31/53 = 0.584906and the first really good one is 7/12. Maybe that's why we divide the scale into 12 equal parts, with the the 7th one up playing a crucial role!
But what if you want a scale that has a good fifth and something else too, like a good third? That's where "generalized" continued fractions come in! I won't tell you what those are.
I also won't tell you about the new revolution linking logic to weak ∞-groupoids. For that you'll have to read these:
15) Martin Hofmann and Thomas Streicher, The groupoid interpretation of type theory, in Sambin, Giovanni, et al, Twenty-five years of constructive type theory, Clarendon Press, Oxford, 1998, pp. 83-111. Also available at http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.37.606
16) Steve Awodey and Michael A. Warren, Homotopy theoretic models of identity types, available as arXiv:0709.0248.
17) Steve Awodey, Pieter Hofstra, Michael A. Warren, Martin-Löf Complexes, available as arXiv:0906.4521.
18) Benno van den Berg and Richard Garner, Types are weak omega-groupoids, available at http://www.dpmms.cam.ac.uk/~rhgg2/Typesom/Typesom.pdf
Addendum: Francesco Toppan writes:
In relation with your recent, interesting, arxiv:0909.0551 paper I would like to signal that division algebras also appear in the N-extended supersymmetric quantum mechanics (in one dimension) for N=1,2,4,8. This is hardly surprising, of course (arXiv:hep-th/0109073 NPB Pr. Sup.). Perhaps slightly more surprising is the fact that the octonionic structure constants enter, as coupling constants, N=8 invariant actions, like e.g. the (1,8,7) model of arXiv:hep-th/0511274 (also in JHEP). In this example the 7 auxiliary fields can be associated with the 7 imaginary octonions, preserving the "octonionic covariance". I should add that the representations of N-extended 1D superalgebra are mathematically very interesting and quite intricate. In the last few years basically two groups, my group and the group of S. Gates and his collaborators, worked out with complementary viewpoints and results several features of these representations: total number of fields, grading of the fields, graph interpretation, connectivity of the graphs, etc. etc. Basic references can be found in hep-th/0010135 (in JMP), hep-th/0610180 (PoS), or typing my name (and Gates'name) in the arXiv. Perhaps you could find these interesting to have a look at.
For more discussion visit the n-Category Café.
A creation of importance can only be produced when its author isolates himself, it is a child of solitude. - Johann Wolfgang von Goethe
© 2009 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|