




|
 
|

|
Next week I'm going to New York to talk about the stuff I've been explaining here lately: electrical circuits and category theory. Then - volcanos permitting - I'll fly to Oxford to attend a course on quantum computation:
1) Foundational Structures in Quantum Computation and Information, May 24-28, 2010, Oxford University, organized by Bob Coecke and Ross Duncan, http://web.comlab.ox.ac.uk/people/Bob.Coecke/QICS_School.html
I look forward to lots of interesting conversations. A bunch of my math pals will be attending - folks like Bruce Bartlett, Eugenia Cheng, Simon Willerton, Jamie Vicary and maybe even my former student Alissa Crans, who lives here in California, but may swing by. I'll talk to Thomas Fischbacher about environmental sustainability and computational field theory, and Dan Ghica about hardware description languages. I also plan to meet Tim Palmer, a physicist at Oxford who works on climate and weather prediction, and one of the people I've been interviewing for the new This Week's Finds. I'm quite excited about that.
(My plan, you see, is to interview people who are applying math and physics to serious practical problems, from global warming and other environmental problems to biotechnology, nanotechnology, artificial intelligence and other potentially revolutionary technologies.)
The weekend after the course, there will be a workshop:
2) Quantum Physics and Logic, May 29-30, 2010, Oxford University, organized Bob Coecke, Prakash Panangaden, and Peter Selinger, http://web.comlab.ox.ac.uk/people/Bob.Coecke/QPL_10.html
Peter Selinger is the guy who got me interested in categories where the morphisms are electrical circuits! I'll be giving a talk in this workshop - you can see the slides here:
3) John Baez, Duality in logic and physics, http://math.ucr.edu/home/baez/dual/
Alas, I've been so busy getting ready for my talks that I don't feel like writing about electrical circuits today. I was going to, but I need a change of pace. So let me say a bit about octonions, higher gauge theory, string theory and hyperdeterminants.
Integers are very special real numbers. But there are also "integers" for the complex numbers, the quaternions and octonions. The most famous are the "Gaussian integers", which are complex numbers like
a + bi
where a and b are integers. They form a square lattice like this:
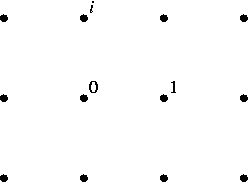
The second most famous are the "Eisenstein integers", which form a hexagonal lattice like this:
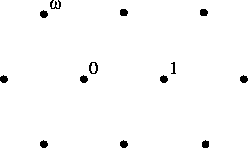
I explained how these lattices are important in string theory back in "week124" - "week126".
People have also thought about various kinds of far less well-known are various kinds of quaternionic and octonionic "integers". To learn about these, there's no better place than the magnificent book by Conway and Smith:
4) John H. Conway and Derek A. Smith, On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry, A. K. Peters, Ltd., Natick, Massachusetts, 2003.
For a little taste, try my summary in "week194", and my review here:
5) John Baez, review of On Quaternions and Octonions, Bull. Amer. Math. Soc. 42 (2005), 229-243. Also available at http://www.ams.org/journals/bull/2005-42-02/S0273-0979-05-01043-8/ and as a webpage at http://math.ucr.edu/home/baez/octonions/conway_smith/
You'll meet the Lipschitz integers and Hurwitz integers sitting inside the quaternions - and the Lipschitzian, Hurwitzian and Gravesian integers sitting inside the octonions. I suspect all these charming names are due to Conway, who has a real gift for terminology. But best of all are the Cayley integers, which form a famous 8-dimensional lattice: the E8 lattice! This gives the densest lattice packing of spheres in 8 dimensions: each sphere touches 240 others.
But you've heard me rhapsodizing about E8 for years. What's new this week? Well, recently I was perusing a draft of a paper on various kinds of quaternionic and octonionic integers, which was kindly sent to me by Norman Johnson. I'm afraid that paper is still top secret, but an interesting issue came up.
People know all the finite subgroups of the unit quaternions, otherwise known as SU(2), the double cover of the 3d rotation group. The most famous of these are:
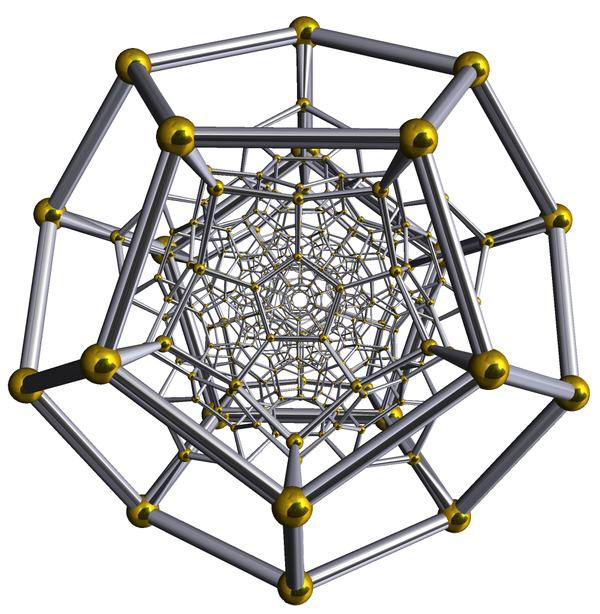
These are the double covers of the rotational symmetry groups of the Platonic solids. Since beautiful structures like this have a way of connecting diverse subjects, you shouldn't be surprised that these groups show up all over in math, from the McKay correspondence and Klein's work on the quintic equation (see "week65" and "week230") to the theory of modular forms (see "week197"). I've talked about the binary icosahedral group many times before: it's also called the 120-cell, and projected down to 3 dimensions it looks like this:
But the best place to learn the classification of finite subgroups of the unit quaternions is the book by Conway and Smith.
For some idiotic reason I'd never pondered the analogous question for the octonions until Norman Johnson brought it up! The unit octonions form a 7-dimensional sphere. They don't form a group, since multiplication of octonions isn't associative. But they form a "loop", which is just like a group but with the associative law dropped. Since they're a smooth manifold, and the group operations are smooth, they form a "Lie loop".
In fact the only spheres that are Lie groups are:
And the only other sphere that's a "Lie loop" is the unit octonions! So we can - and should! - ask: what are the finite subloops of the unit octonions?
Michael Kinyon, an expert on loops, quickly provided two references that settle the question:
6) R. T. Curtis, Construction of a family of Moufang loops, Math. Proc. Cambridge Philos. Soc. 142 (2007), 233-237.
7) P. Boddington and D. Rumynin, On Curtis' theorem about finite octonionic loops, Proc. Amer. Math. Soc. 135 (2007), 1651-1657. Available at http://www.ams.org/journals/proc/2007-135-06/S0002-9939-07-08707-2/
There are no huge surprises here. The most exciting finite subloop has 240 elements: it consists of the Cayley integers of length 1, otherwise known as the root vectors of E8. You've probably seen this thing:

The rest of the finite subloops are either finite subgroups of the unit quaternions or "doubles" of these. No exotic beasts I hadn't dreamt of. But it's very nice to know the full story!
I also have some other news on the octonionic front. John Huerta and I wrote a second paper on division algebras and supersymmetry, where we explain how to construct the "Lie n-superalgebras" that govern classical superstring and super-2-brane theories:
8) John Baez and John Huerta, Supersymmetry and division algebras II, available as arXiv:1003.3436.
As you may know, Lie groups and their Lie algebras are incredibly important in gauge theory, which describe how particles change when you move them around. Lately people have been developing "higher gauge theory", which does the same job for strings and higher-dimensional membranes. For strings we need Lie 2-groups and their Lie 2-algebras. Lie 2-groups are like Lie groups except that they're categories instead of sets... and similarly for Lie 2-algebras. Go up one more dimension and you need math based on 2-categories. So, for 2-branes, which look like soap bubbles instead of loops of string, you need Lie 3-groups and their Lie 3-algebras. Etcetera.
So, the race is on to construct, classify and understand Lie n-groups and Lie n-algebras - and redo all of geometry to take advantage of these higher structures! For an easy introduction, try:
9) John Baez and John Huerta, An invitation to higher gauge theory, available as arXiv:1003.4485.
But for supersymmetric theories, geometry based on manifolds isn't enough: we need supermanifolds. The world is made of bosons and fermions, and supersymmetry is an attempt to unite them. So, a supermanifold has ordinary "even" or "bosonic" coordinate functions that commute with each other, but also "odd" or "fermionic" coordinate functions that anticommute. For the last few decades people have been redoing geometry using supermanifolds. As part of this, they've done a lot of work to construct, classify and understand Lie supergroups and their Lie superalgebras.
Superstring theory combines supersymmetry and higher-dimensional membranes in a beautiful way. It's never made any predictions about the real world, and it may never succeed in doing that. But it's been a real boon for mathematicians. And here's another example: we can now enjoy ourselves developing a theory of Lie n-supergroups and their Lie n-superalgebras!
I might feel guilty indulging in such decadent pleasures, were it not that I plan to start work on more practical projects. But having spent years thinking about division algebras and higher gauge theory, it was irresistible to combine them - especially since my student John Huerta has a knack for this stuff.
And here's what we discovered:
3, 4, 6 and 10 - these are two more than the dimensions of the real numbers, complex numbers, quaternions and octonions. I've discussed this pattern many times here. But then we discovered something else:
4, 5, 7 and 11 - these are three more than the dimensions of the real numbers, complex numbers, quaternions and octonions! And the 11d case is related to "M-theory" - that mysterious dream you've probably heard people muttering about.
You might ask if the pattern keeps going on, like this:
But some calculations by Tevian Dray and John Huerta, together with a lot of physics lore, suggest that the pattern does not keep going on - at least not for the most exciting case, the octonionic case. You can see what I mean by looking at the "brane scan" in this classic paper by Duff:
10) Michael J. Duff, Supermembranes: the first fifteen weeks, Classical and Quantum Gravity 5 (1988), 189-205. Also available at http://ccdb4fs.kek.jp/cgi-bin/img_index?8708425
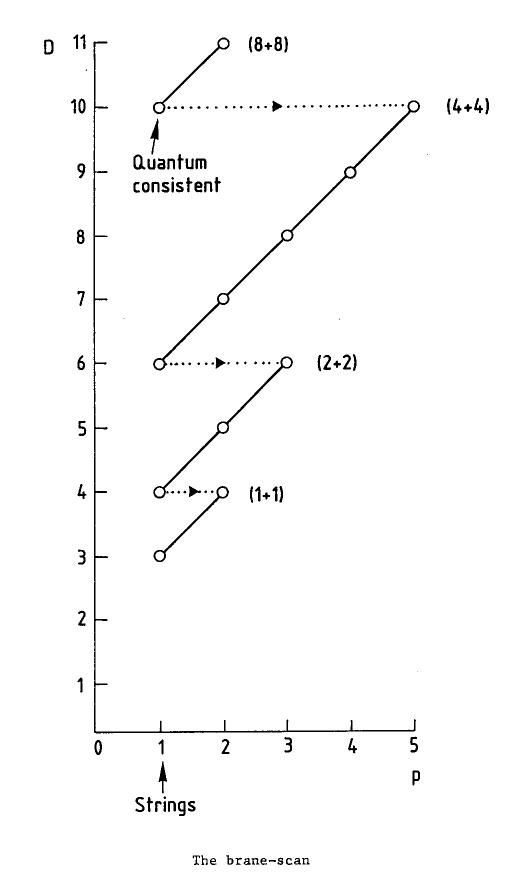
The story seems to fizzle out after 11 dimensions. And that's part of what intrigues me about division algebras and related exceptional structures in math: the funny fragmentary patterns that don't go on forever.
Recently Peter Woit criticized Duff for some remarks in this article:
11) Michael Duff, Black holes and qubits, CERN Courier May 5, 2010. Available at http://cerncourier.com/cws/article/cern/42328
12) Peter Woit, Applying string theory to quantum information theory, http://www.math.columbia.edu/~woit/wordpress/?p=2925
Duff's article describes how he noticed some of the same math showing up in superstring calculations of black hole entropy and patterns of quantum entanglement between qubits. This leads into some nice math involving octonions and related exceptional structures like the Fano plane and Cayley's "hyperdeterminants".
Unfortunately, Duff gets a bit carried away. For example, he says that string theory "predicts" the various ways that three qubits can be entangled. Someone who didn't know physics might jump to the conclusion that this is a prediction whose confirmation lends credence to string theory as a description of the fundamental constituents of nature. It's not!
I also doubt that "superquantum computing" is likely to be practical... though I've read interesting things about supersymmetry in graphene, so I could wind up eating my words.
On the other hand, the math is fascinating. For details, try these papers:
13) Akimasa Miyake and Miki Wadati, Multipartite entanglement and hyperdeterminants, Quant. Info. Comp. 2 (2002), 540-555. Also available as arXiv:quant-ph/0212146.
14) Michael J. Duff and S. Ferrara, E7 and the tripartite entanglement of seven qubits, Phys. Rev. D 76 025018 (2007). Also available as arXiv:quant-ph/0609227.
15) Michael J. Duff and S. Ferrara, E6 and the bipartite entanglement of qutrits, Phys. Rev. D 76 124023 (2007). Also available as arXiv:0704.0507.
or this very nice recent one:
16) Bianca L. Cerchiai and Bert van Geemen, From qubits to E7, available as arXiv:1003.4255.
Since I've spent a lot of time talking about the Fano plane, the octonions, and exceptional groups like E6, E7 and E8, let me say just a word or two about hyperdeterminants.
In the 1840's, after his work on determinants, Arthur Cayley invented a theory of "hyperdeterminants" for 2 × 2 × 2 arrays of numbers. They're a bit like determinants of 2 × 2 matrices, but more complicated. They lay dormant for about a century, but were recently revived by three bigshots: Gel'fand, Kapranov and Zelevinsky. I never understood them, but when Woit called them "extraordinarily obscure", it was like waving a red flag in front of a bull. I charged forward... and now I sort of understand them, at least a little.
Suppose we have a 2 × 2 matrix of complex numbers. We can think of this as an element of the Hilbert space
C2 ⊗ C2
so we get a linear functional
C2 ⊗ C2 → C
sending any vector to its inner product with this element. We can then regard this linear functional as a function
f: C2 × C2 → C
that's linear in each argument. Is there a nonzero point in C2 × C2 where the gradient of f vanishes? The answer is yes if and only if the determinant of our 2 × 2 matrix is zero!
Next, suppose we have a 2 × 2 × 2 array of complex numbers. We can think of this as an element of the Hilbert space
C2 ⊗ C2 ⊗ C2
so we get a linear functional
C2 ⊗ C2 ⊗ C2 → C
sending any vector to its inner product with this element. We can then regard this linear functional as a function
f: C2 × C2 × C2 → C
that's linear in each argument. Is there a nonzero point in C2 × C2 × C2 where the gradient of f vanishes? The answer is yes if and only if the hyperdeterminant of our 2 × 2 × 2 array is zero!
Here's another way to think about it. Suppose you have a quantum system made of 3 subsystems, each described by a 2d Hilbert space. The Hilbert space of the whole system is thus
C2 ⊗ C2 ⊗ C2
The hyperdeterminant is a function on this space that can be thought of as measuring how correlated - or to use a bit of jargon, "entangled" - the 3 subsystems are. In particular, if we look at unit vectors modulo phase, we get the projective space CP7. The group
GL(2,C) × GL(2,C) × GL(2,C)
acts on this. There's an open dense orbit, coming from the vectors whose hyperdeterminant is nonzero. These states are quite entangled, as you'd expect: entanglement is not an exceptional situation, it's generic. And then there are various smaller orbits, going down to the 1-point orbit coming from vectors like
u ⊗ v ⊗ w
These describe states with no entanglement at all!
We can make what I'm saying a bit more precise at the expense of a little more math. The polynomial functions on C2 ⊗ C2 ⊗ C2 that are invariant under the action of SL(2,C) × SL(2,C) × SL(2,C) form an algebra, and this algebra is generated by the hyperdeterminant, which is a homogeneous cubic polynomial. (Why did I switch from GL(2,C) to SL(2,C)? Because the hyperdeterminant is not invariant under the bigger group GL(2,C) × GL(2,C) × GL(2,C). However, it comes close: it gets multiplied by a scalar in a simple way.)
If we try to generalize this idea to tensor products of more spaces, like C2 ⊗ C2 ⊗ C2 ⊗ C2 we typically get an algebra that's not generated by a single polynomial. The same happens if we jack up the dimension, for example replacing C2 by C9. So, the situations where a single polynomial does the job are special.
As an extra lure, let me add that you can write the Lagrangian for a string in (2+2)-dimensional spacetime using 2 × 2 × 2 hyperdeterminants! The formula is very pretty and simple:
17) Michael J. Duff, Hidden symmetries of the Nambu-Goto action, Phys. Lett. B641 (2006), 335-337. Also available as arXiv:hep-th/0602160.
This being the 21st century, there is even a blog on hyperdeterminants:
18) Hyperdeterminacy, http://hyperdeterminant.wordpress.com/2008/09/25/hello-world/
The author begins with some introductory posts which are definitely worth reading, so I've linked to the first of those. He expresses the worry that "this may be turn out to be one of the least read blogs in the blogosphere". Go visit, leave a comment, and prove him wrong!
Addenda: On August 8th 2010, I received the following mail from Péter Lévay, who has allowed me to quote it here:
Dear John,For more discussion, visit the n-Category Café.I used to read your fascinating blog. Recently I have come across your "week298" post (14 May) concerning hyperdeterminants and reflections on a paper by Duff which appeared in CERN Courier on the black hole qubit correspondence.
Since I know that you are really fascinated by octonions, Freudenthal systems, etc., with this mail I intend to draw your attention to papers of mine connected to the stuff of your "week298" post. Moreover, I would also like to add some further hints (which Duff does not mention) why this analogy is worth working out further.
Originally I used to work on the field of quantum entanglement, and group theoretical and geometrical methods in quantum physics. My paper:
19) Péter Lévay, The twistor geometry of three-qubit entanglement, available as arXiv:quant-ph/0403060.
on the "Cayley" hyperdeterminant, twistors and three qubit entanglement was the one that motivated originally Duff's work (as he mentions in the CERN Courier). Later I have written another paper on the four qubit case (hyperdeterminant):
20) Péter Lévay, On the geometry of four qubit invariants, available as arXiv:quant-ph/0605151.
After Duff's and Kallosh and Linde's paper I have shown that the black hole qubit analogy also works for issues concerning DYNAMICS. I have shown that the attractor mechanism (a process used for moduli stabilization on the BH horizon) can be rephrased in this picture as a distillation procedure of GHZ-like states:
21) Péter Lévay, Stringy black holes and the geometry of entanglement, available as arXiv:hep-th/0603136.
Péter Lévay, A three-qubit interpretation of BPS and non-BPS STU black holes, available as arXiv:0708.2799.
Péter Lévay and Szilárd Szalay, The attractor mechanism as a distillation procedure, available as arXiv:1004.2346.
The physical nature of these moduli, charge and warp factor dependent "states" (or whether is it legitimate to call them states at all) is, however, still unclear.
Independently of Duff and Ferrara during the summer of 2006 I worked out the E7 tripartite entanglement of seven qubits picture. My paper came out later because I have bogged down on some maths details (I also wanted to see the E7 generators in the 56 dim rep. acting as qubit gates - without success!) However, the idea that this curious type of entanglement is related to the structure of the Fano plane appears first in this paper:
22) Péter Lévay, Strings, black holes, the tripartite entanglement of seven qubits and the Fano plane, available as arXiv:hep-th/0610314.
Here I made the conjecture that Freudenthal systems and issues concerning the magic square could be relevant to further developments of the black hole qubit analogy, initiating the nice study of Duff et al, culminating in their valuable Phys. Reports paper.
In the meanwhile with my student we have shown that Freudenthal systems are capable of giving hints for solving the classification problem of entanglement classes for systems consisting of special types of indistinguishable constituents (fermions and bosons). The black hole entropy formulas of string theory and supergravity also gave suggestions how to define sensible (tripartite) entanglement measures for these systems:
23) Péter Lévay and Péter Vrana, Three fermions with six single particle states can be entangled in two inequivalent ways, available as arXiv:0806.4076.
Péter Lévay and Péter Vrana, Special entangled quantum systems and the Freudenthal construction, available as arXiv:0902.2269.
Apart from these studies after realizing the relevance of finite geometric ideas with a Slovak co-worker Metod Saniga we have shown that the structure of the E6 and E7 invariants giving rise to black hole entropy formulas are related to generalizations of Mermin Square like configurations, and generalized polygons. Our studies motivated partly the nice paper of van Geemen and B. L Cerchiai you mention in your post ("From qubits to E7"). Since the finite geometric structures relevant to the black hole qubit correspondence turned out to be just geometric hyperplanes of incidence geometries for n-qubit systems, we conducted a mathematical study on the structure of such hyperplanes giving rise to another incidence geometry: the Veldkamp space. The nice maths results can be found in:
24) Péter Vrana and Péter Lévay, The Veldkamp space of multiple qubits, available as arXiv:0906.3655.
Such notions as symplectic structure, quadratic forms, transvections, and the group Sp(2n,2) connected to n-qubit systems and black holes appear here. The language of this paper is similar to the van Geemen paper.
Recently I have shown that certain solutions of the STU model living in 4D and coming from one sector of the E7(7) invariant N=8 SUGRA Duff mentions in his paper in connection to three qubits, is really a model living in 3D coming from a coset of E8(8) related to FOUR QUBITS. In this paper I have given hints that the classification problem for four qubits can be translated to the classification problem of black hole solutions (BPS and non BPS, extremal and even possibly non extremal).
25) Péter Lévay, STU black holes as four qubit systems, available as arXiv:1004.3639.
(The idea that four qubit systems show up in STU truncations first appeared in my Fano-E7 paper. This is related to the structure of a coset of SO(4,4), with triality making its debut via permutation of the qubits.)
Based on the results of this paper the challenge to relate the BH classification problem based on four qubit systems by fitting together the existing results in the literature was recently taken up by Duff et al.
I hope that these results add some useful hints to update the picture on the black hole qubit correspondence.
I think that the main virtue of this field is that fascinating maths (like octonions, Freudenthal systems, finite geometries etc.) will finally makes its debut to understanding quantum entanglement better. On the string theory side such studies might initiate some new way of looking at existing results in the field of stringy black hole solutions.
Of course finding the underlying physics (if any) is still out there!
With best regards,
Peter Levay
Department of Theoretical Physics
Institute of Physics
Budapest University of Technology
HUNGARY
Quaternions appear to exude an air of nineteenth century decay, as a rather unsuccessful species in the struggle-for-life of mathematical ideas. Mathematicians, admittedly, still keep a warm place in their hearts for the remarkable algebraic properties of quaternions but, alas, such enthusiasm means little to the harder-headed physical scientist. - Simon L. Altmann
© 2010 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|