




|
 
|

|
Two weeks ago I went to Oxford to attend a school on Quantum Information and Computer Science, and then a workshop on Quantum Physics and Logic. So, I'll start by telling you about those.
I'll show you where you can see videos of the talks. You can learn about string diagrams and see how people use these in quantum physics. You can even watch a program called "Quantomatic" automatically carry out some string diagram computations! I'll explain how classical structures give Frobenius algebras, and how complementary classical structures almost give Hopf algebras. And then I'll tell you about Aaron Fenyes' no-cloning theorem for classical mechanics. There was a lot more to the conference, but that's all I have the energy for.
Why? Well, after I came home, my friend the combinatorist Bill Schmitt paid me a visit. He told me a lot of interesting stuff about about "pre-Lie algebras". These are algebraic gadgets with deep connections to trees, operads, and the work of Connes and Kreimer on renormalization in quantum field theory. So, I want to tell you about that stuff, too.
Let's get started. You can see all the talks here:
1) Oxford Quantum Talks Archive,
http://www.comlab.ox.ac.uk/quantum/content/
QICS Spring School 2010, talks available at http://www.comlab.ox.ac.uk/quantum/content/events.html#QICS%20spring%20school%202010
Quantum Physics and Logic 2010, talks available at http://www.comlab.ox.ac.uk/quantum/content/events.html#Quantum%20Physics%20and%20Logic%202010
I've been using pictures called "string diagrams" for a long time here on This Week's Finds, and I've tried to explain them, but these talks give a nice systematic treatment:
2) Introduction to monoidal categories and graphical calculus.
Lecture 1 by Chris Heunen, available at
http://www.comlab.ox.ac.uk/quantum/content/1005005/
Lecture 2 by Jamie Vicary, available at
http://www.comlab.ox.ac.uk/quantum/content/1005010/
With the help of these diagrams we can think about many, many things. In particular, we can use them to describe processes in quantum mechanics. Feynman diagrams are an example. But now people in quantum information theory are using them in very different ways. For example, they're using them to study "classical structures" in quantum mechanics.
What's a classical structure? The basic idea is simple. You can't "clone a quantum". In other words, you can't build a "quantum copying machine" where you feed in a quantum system in an arbitrary state and have two identical copies pop out, both in the same state.
Why not? Well, you could try to measure everything about your system and make a copy where all those measurements have the same values. But you can never succeed! Measuring one thing will change the values of other things you already measured, in uncontrollable random ways. So you can never know everything about your system... not all at once! So, it's impossible to make an exact copy.
However, sometimes measuring one thing does not mess up the value of something else you measured. Quantities that get along this way are called "commuting" observables. A "classical structure" is a set of commuting observables that's as big as possible. And for each classical structure, we can build a copying machine that works for these observables.
For example, there's no way to take an electron, stick it in a copying machine, and duplicate everything about it. You can measure the spin of an electron along any axis. If you measure the spin along the x axis you get one of two results: "up" or "down". Similarly for the spin along the y axis. However, measuring the spin along the x axis messes up its spin along the y axis.
So, you can build a machine that takes an electron, measures its spin along the x axis, and spits out two electrons in that same state: either "spin-up" or "spin-down" along the x axis. But if you put an electron with spin up along the y axis in this machine, it will not be correctly duplicated.
In this example, there's a classical structure consisting of the spin along the x axis, and every function of this observable... but this classical structure does not include the spin along the y axis.
Here's a quick sketch of how the math works. If you're a mathematician, this should be far less confusing than the prose you just suffered through. In fact, you may be left wondering why I turned such simple math into such murky prose. But that's typical of quantum mechanics: the math is crystal clear, but when you try to explain how it describes the real world, it starts sounding mysterious.
Suppose H is a Hilbert space. If we were trying to build a quantum copying machine, it would be nice to have a linear operator like this:
H → H ⊗ H
ψ |→ ψ ⊗ ψ
But this operator is not linear, because doubling ψ would quadruple ψ ⊗ ψ.
Life gets easier when we have a classical structure. An "observable" in quantum mechanics is a self-adjoint operator. So, a "classical structure" is a maximal set of commuting self-adjoint operators. If H is finite-dimensional, we can get any classical structure from an orthonormal basis. How? Just take all the self-adjoint operators that are diagonal in that basis.
If you pick an orthonormal basis for H, say ei, there's a unique linear operator that duplicates states in that basis:
H → H ⊗ H
ei |→ ei ⊗ ei
So, this is how a classical structure gives a "duplication operator".
Here's where the string diagrams come in. We can draw our duplication operator in a funny symbolic way like this:
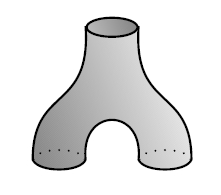
This is a picture of a 2d surface where one circle comes in and two go out - a kind of metaphor for duplication. We'll see why it's a good metaphor in a minute.
There's another thing we can do after we've picked an orthonormal basis for our Hilbert space H: we can define a "deletion operator"
H → C
ei |→ 1
which sends each state in the basis to the number 1. Here C is the complex numbers, a 1-dimensional Hilbert space. We can think of C as a kind of "garbage bin", and think of our operator as "throwing out" states in our basis. We can draw it as a cup-shaped thing, like this:
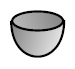
This is not really a picture of a garbage bin, though it looks like that too. It's a picture of a 2d surface where one circle comes in and none go out!
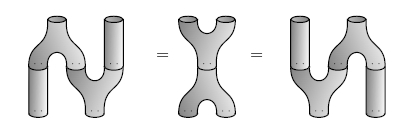
Now, the cool part is that our duplication and deletion operators satisfy rules that look very intuitive in terms of these pictures. For example, if we duplicate a state and then duplicate one of the copies, it doesn't matter which copy we duplicate. And if we duplicate a state and then delete either copy, it's the same as not doing anything:
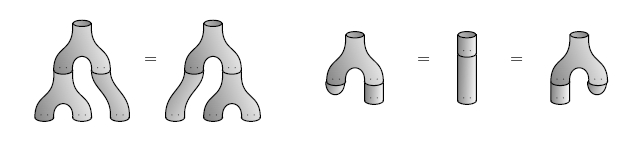
These rules are "topologically true": to get one of these equations, we just take one picture and wiggle it and warp it until it looks like another.
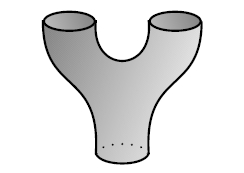
There are a bunch of other rules. Almost all of them are topologically true - exactly what you'd dream up by playing around with pictures of 2d surfaces. But to write down these rules, you need to notice that any operator between Hilbert spaces has an adjoint going the other way. So, besides duplication:
H → H ⊗ H
we have its adjoint:
H ⊗ H → H
which we draw just like duplication, except upside-down:
and besides deletion:
H → C
we have its adjoint:
C → H
which we draw just like deletion, except upside-down:

In math we call these four operators the "multiplication":
m: H ⊗ H → H
the "unit":
i: C → H
the "comultiplication":
Δ: H → H ⊗ H
and the "counit":
e: H → C
And we can summarize all the rules these operators obey by saying that H is a "special commutative dagger-Frobenius algebra". That's a mouthful, but as I said, almost all these rules come from topologically allowed manipulations on 2d surfaces.
What are these rules? Well, I listed the rules for a Frobenius algebra back in "week268". There are the "associative law" and the "left and right unit laws":
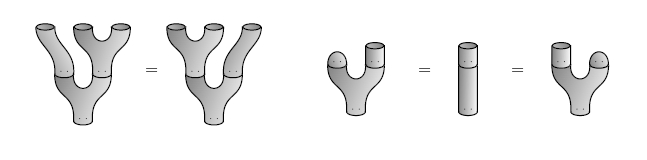

We say a Frobenius algebra is "special" if it obeys yet another law, which I'll show you later. So the only extra thing you need to know is what's a "dagger-Frobenius" algebra. And that's just a Frobenius algebra that's also a Hilbert space, where the multiplication and unit are adjoint to the comultiplication and counit! For more, try these papers:
3) Bob Coecke and Dusko Pavlovic, Quantum measurements without sums, in The Mathematics of Quantum Computation and Technology, eds. Chen, Kauffman and Lomonaco, Chapman and Hall/CRC, New York, pp. 559-596. Also available as arXiv:quant-ph/0608035.
4) Jamie Vicary, Categorical formulation of quantum algebras, available as arXiv:0805.0432.
5) Bob Coecke, Dusko Pavlovic and Jamie Vicary, A new description of orthogonal bases, available as arXiv:0810.0812
But what's really going on with all these pictures of 2d surfaces? You see them a lot in topological quantum field theory. Indeed, in "week268" I explained that a commutative Frobenius algebra is exactly what we need to get a 2d topological quantum field theory, or TQFT for short. This is a way of making precise the idea that any of these pictures gives a well-defined operator - and warping or wiggling the picture doesn't change the operator.
Even better, a commutative dagger-Frobenius algebra is exactly what we need to get a "unitary" 2d TQFT. This means that the upside-down version of a given picture gives the adjoint operator.
So, we're seeing a curious fact:
This sounds like it should be important, because it links two subjects with very different flavors: the foundations of quantum mechanics, and topological quantum field theory. But I have no idea what it really means.
Maybe you can help me! But before you try your hand at this problem, I should warn you that we don't get all unitary 2d TQFTs from classical structures - because we don't get all commutative dagger-Frobenius algebras. We only get the "special" ones, which obey this extra rule:
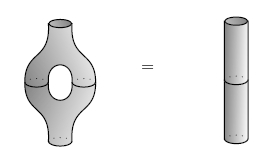
This rule is not topologically true. Indeed when it holds, our 2d TQFT is completely insensitive to how many handles our surface has. That makes it sort of boring.
For a closed surface, the number of handles is called the "genus". So, the real puzzle is to understand this more mysterious slogan:
I've been mulling this over for about a year now, with no great insights. Mathematically it's almost trivial. But physically, I can't tell if it's the tip of an interesting iceberg, or just a coincidence.
These talks offered some extra clues:
6) Ross Duncan, Convexity, categorical semantics and the foundations of physics, video available at http://www.comlab.ox.ac.uk/quantum/content/1005102/
7) Chris Heunen, Complementarity in categorical quantum mechanics, video and slides available at http://www.comlab.ox.ac.uk/quantum/content/1005115/
8) Simon Perdrix, Classical-quantum graphical calculus, video available at http://www.comlab.ox.ac.uk/quantum/content/1005015/
For more details, try these papers:
9) Bob Coecke, Eric Oliver Paquette and Dusko Pavlovic, Classical and quantum structuralism, available as arXiv:0904.1997.
10) Bob Coecke and Ross Duncan, Interacting quantum observables: categorical algebra and diagrammatics, available as arXiv:0906.4725.
11) Bob Coecke, Quantum picturalism, available as arXiv:0908.1787.
12) Bob Coecke and Simon Perdrix, Environment and classical channels in categorical quantum mechanics, arXiv/1004.1598.
Among other things, these papers say what you can do with a classical structure. You can do a bunch of things - and you can do them all very generally, because you can do them using just pictures. So, you don't need to be working in the category of finite-dimensional Hilbert spaces: any "dagger-compact category" will do. You can define a special commutative dagger-Frobenius algebra in any such category, and this gives a very general concept of classical structure.
This is the sort of thing that makes category theorists drool. But I will restrain myself! I won't work in such generality. I'll just work with finite-dimensional Hilbert spaces, and just sketch a few things we can do with classical structures. I won't even explain how we can do them just using pictures... even though that's the really cool part.
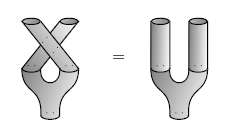
For starters, every classical structure determines a "phase group". If the classical structure comes from an orthonormal basis in the way I've described, its phase group consists of all unitary operators that are diagonal in this basis. But the cool part is that we can define this group just using pictures, and prove it's abelian, and so on.
We can also use pictures to define "complementarity". In physics we say position and momentum are complementary because if you know everything about one, you cannot know anything about the other. But we can also say what it means for two classical structures to be complementary. For a finite-dimensional Hilbert space, any classical structure comes from an orthonormal basis - and two of them are "complementary" if they come from "mutually unbiased" bases, meaning bases ei and fj such that
|<ei,fj>|
is independent of i and j. This means that if you know precisely which state ei your system is in, it has equal chances of being found in any of the states fj.
So, for example, the spin-up and spin-down states of an electron as measured along the x axis form one orthonormal basis. The spin-up and spin-down states as measured along the y axis form another. And these bases are mutually unbiased. So, knowing everything about the spin along the x axis tells you nothing about the spin along the y axis. And vice versa!
When we have two complementary classical structures, we get two ways of making our Hilbert space into a Frobenius algebra. And these are related in a cool way: if we use the multiplication of the first, and the comultiplication of the second, we almost get a "Hopf algebra"! If we had a Hopf algebra, this relation would hold:
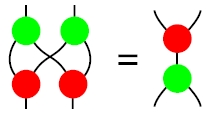
where we write the multiplication of our first Frobenius algebra as a red dot, and the comultiplication of the second as a green dot. But in fact this holds only up to a constant factor, so we get a "scaled Hopf algebra". I think this is fascinating because there's a constant interplay between Frobenius algebras and Hopf algebras in mathematics, and here's yet another example.
Now, if you like these pictures, you've got to see "Quantomatic" in action:
13) Lucas Dixon, Quantomatic demo, video available at http://www.comlab.ox.ac.uk/quantum/content/1005019
14) Lucas Dixon, Ross Duncan, Aleks Kissinger and Alex Merry, Quantomatic, http://dream.inf.ed.ac.uk/projects/quantomatic/
This is a program that automatically carries out calculations involving these pictures that I've been drawing! It's a lot of fun. If you know quantum computation, you'll see that we can describe a lot of quantum logic gates, like controlled not gates and Hadamard gates, using these pictures. And if you know 2-categories, you'll realize that the processes of rewriting diagrams are actually 2-morphisms in a 2-category! So higher category is sneaking in to the subject here. I bet we'll see a lot more of it in years to come.
There were many more interesting talks, but I'm running out of energy, so I just want to say one more thing about "cloning":
15) Aaron Fenyes, There's no cloning in symplectic mechanics, available at http://math.ucr.edu/home/baez/dual/no-cloning.pdf
This paper argues that the laws of classical mechanics make it impossible to build a "cloning machine". If we had such a machine, we could put two boxes with balls in them into slots on top of the machine. The machine would copy the position and velocity of the first ball over to the second one. When we were done, the second ball would be a "clone" of the first: a perfect copy.
Let me be a bit more precise. The boxes and the balls inside them are identically made. The first ball, the one we want to clone, has an arbitrary position and velocity. Well, of course its position is somewhere in the box! And if you like, we can say it's going no faster than 10 miles per hour. The second ball starts out in some fixed state. Let's say it has zero velocity and it's sitting right in a little dent in the middle of the box.
We pop the boxes into the machine. The machine can open the tops of the boxes and insert sensors. When we press a big red button, the machine measures the position and velocity of the first ball. It then does whatever it wants, but after a while two boxes come out of the bottom of the machines... and then a bell rings.
And when the bell rings, both balls have the same position and velocity that the first ball had when you pressed the button!
A "no-cloning theorem" says you can't build a machine like this, given some assumptions on the laws of physics. The original no-cloning theorem was due to Wooters and Zurek:
16) W. K. Wootters and H. D. Zurek, A single quantum cannot be cloned, Nature, 299 (1982), 802-803.
You can see a statement and proof here:
17) Wikipedia, No-cloning theorem, http://en.wikipedia.org/wiki/No-cloning_theorem
This was a quantum no-cloning theorem. In fact it was very general: it wasn't about balls in boxes, it was about any quantum system where states are described by unit vectors in a Hilbert space and processes are described by unitary operators.
There have been many no-cloning theorems since then, but what's new about Aaron Fenyes' result is that it applies to classical mechanics. Again, it's very general: it's about any classical system where states are described by points in a symplectic manifold, and processes are described by symplectomorphisms.
If that sounds scary, well, be reassured that most classical mechanics problems fit into this framework. There are some that can't, but I bet Fenyes' result can be generalized to cover a lot of those, too.
So, the big question is: how does this result square with the widely shared intuition that we can copy classical information: that we can exactly measure the position and momentum of a ball, say, and get two balls into that state?
I don't know the answer, but I'd like to - so let me know if you figure it out. Part of the problem is that when we use phrases like "classical structure" in our study of quantum mechanics, we are not talking about full-fledged classical mechanics, in which symplectic structures are important. But even after we work through this semantic issue, there's a physics issue left to ponder.
After I got back to Riverside, my friend Bill Schmitt visited me. As usual, we spent long evenings listening to music and talking about math. I told you about our last get-together in "week265". Back then, he told me about an amazing 588-page paper on Hopf algebras, combinatorics and category theory by Aguiar and Mahajan. By now that paper has grown into an 836-page book:
18) Marcelo Aguiar and Swapneel Mahajan, Monoidal functors, species and Hopf algebras, available at http://www.math.tamu.edu/~maguiar/a.pdf
In his preface, André Joyal calls it "a quantum leap towards the mathematics of the future". Check it out!
Now Bill is working with Aguiar on developing this theory further. There are some marvelous ideas here... but I'd rather tell you about something else: pre-Lie algebras.
The name "pre-Lie algebra" suggests that we're about to do some "centipede mathematics". That's the cruel sport where you take a mathematical concept and see how many legs you can pull off and have it still walk. For example: you take the concept of group, remove the associative law and the identity element, obtaining the concept of "quasigroup"... and then see if there are still any theorems left.
A "pre-Lie algebra" sounds like a Lie algebra with some legs pulled off. But actually it's an associative algebra with some legs pulled off! Any associative algebra gives a Lie algebra - but you don't need the full force of the associative law to play this game. It's enough to have pre-Lie algebra.
That doesn't sound too interesting. But Bill convinced me that pre-Lie algebras are important. They were first named by Gerstenhaber:
19) M. Gerstenhaber, The cohomology structure of an associative ring, Ann. Math. 78 (1963), 267-288.
who showed that the Hochschild chain complex of any ring, with grading shifted down by one, is a graded pre-Lie algebra. Later it was noticed that pre-Lie algebras show up in the combinatorics of trees, and are implicit in this old paper by Cayley:
20) Arthur Cayley, On the theory of the analytical forms called trees, Phil. Mag. 13 (1857), 172-176.
The fun really starts when we relate these ideas to quantum field theory and operads...
...but first things first! The definition is simple enough. A pre-Lie algebra is a vector space A equipped with a bilinear product such that
[L(a), L(b)] = L([a,b])
for every a, b in A.
Huh? Here L(a) stands for left multiplication by a:
L(a) b = ab
and the brackets denote commutators, so
[L(a), L(b)] = L(a) L(b) - L(b) L(a)
and
[a,b] = ab - ba
Putting together these formulas, we see the a pre-Lie algebra is vector space equipped with a bilinear product satisfying this scary equation:
a(bc) - b(ac) = (ab)c - (ba)c
Now, it's obvious that every associative algebra is a pre-Lie algebra: just take this scary equation and erase the parentheses, and you'll get something true. But not every pre-Lie algebra is associative. I'll give you some examples in a minute.
When we have an associative algebra, we get a Lie algebra with this bracket:
[a,b] = ab - ba
But we also get a Lie algebra this way from any pre-Lie algebra! That's why they're called "pre-Lie". To check this, take the scary equation above and use it to derive the Jacobi identity:
[[a,b],c] + [[b,c],a] + [[c,a,],b] = 0
Try it! It's fun. Honest!
Okay - so pre-Lie algebras are a cute generalization of associative algebras which are still good enough to give Lie algebras. But now you probably want me to explain how pre-Lie algebras show up in nature. I'll give three examples. The first is from geometry. The second is from quantum field theory. The third involves operads.
First, given a manifold with a flat torsion-free connection D on its tangent bundle, we can make the space of tangent vector fields into a pre-Lie algebra by defining
vw = Dv w
Second, Connes and Kreimer noticed a certain amazing group that plays an important role in the renormalization of quantum field theories:
21) Alain Connes and Dirk Kreimer, Hopf algebras, renormalization and noncommutative geometry, Commun. Math. Phys. 199 (1998), 203-242. Also available as arXiv:hep-th/9808042.
They built this group from Feynman diagrams. How? As you probably know, it's good to build groups starting from Lie algebras. And that's basically what they did. But what Lie algebra did they use?
The answer is easy if you know about pre-Lie algebras. But first I want to sketch the usual story. This is much more lengthy and technical... but I want to run you through it, so you can fully appreciate the elegance of the slick approach.
In the usual approach, you need to know that any Lie algebra gives rise to something called a "universal enveloping algebra". This is a cocommutative Hopf algebra, so its dual - defined in a careful way - is a commutative Hopf algebra. Connes and Kreimer started by getting their hands on this commutative Hopf algebra. Then they worked back to the Lie algebra.
To get their commutative Hopf algebra, they began with vector space whose basis consists of Feynman diagrams. But they also found it helpful to consider a simpler problem, where you start with a vector space whose basis consists of rooted forests.
A "rooted tree" looks like this:
o o o o
\|/ /
o o
\ /
o
|
o
The vertex at the bottom is called the "root". A finite
collection of rooted trees is called a "rooted forest":
o o o o
\| / |
o o o o o
\ / \ / |
o o o o o
| | \|/
o o o o
Let me show you how to take the vector space whose basis consists of all rooted forests, and make that into a commutative Hopf algebra. To do this, we need to give our vector space a multiplication and a comultiplication. And it's enough to say how these work on basis vectors, which are rooted forests.
To multiply two rooted forests, we simply set them side by side to get a new rooted forest. This multiplication is obviously associative. It's also commutative, since we don't care about any "ordering" or "planar structure" on our rooted forests.
In short, multiplication is boring. The fun part is comultiplication! To comultiply a rooted forest, we go through all ways of slicing it in a roughly horizontal way. Each slice gives two rooted forests: one below the slice, and one above. Then we form a big sum, where each slice contributes a term
(below) ⊗ (above)
where the first factor is the forest below the slice, while the second is the forest above the slice. You can see pictures of how this works in Connes and Kreimer's paper. The forest below the slice is sometimes called the "pruned forest", while the forest above is called the "fallen branches". If you've ever trimmed trees, that should give you the idea.
Starting from this Hopf algebra, you can get a Lie algebra. But there's a vastly quicker way to get this Lie algebra... if you know about pre-Lie algebras, that is. It's:
That's what I call slick. Instead of paragraphs of theorems and pictures, a single devastatingly efficient phrase.
But of course we need to see what's lurking in this phrase. Where did the rooted forests go? To answer this, you need to check that the free pre-Lie algebra on one generator has a basis given by rooted trees. Then its universal enveloping algebra will have a basis given by rooted forests!
So, the key question is: why does the free pre-Lie algebra on one generator have a basis given by rooted trees? Let me quickly sketch the answer Bill gave me. This may sound a bit cryptic, but I want to write it down before I forget.
Suppose you have rooted trees a and b and you attach a to b. More precisely: suppose you connect the root of a to some vertex of b using a new edge, forming a new rooted tree. You can do this in lots of ways, so you'll get a linear combination of trees, say ab. And this how multiplication in the free pre-Lie algebra on one generator works!
We can summarize this as follows:
ab = a
|
b
Here the picture stands for any way of attaching a to b. We
should really sum over all of them.
When you form a product like a(bc), different things can happen. We can summarize the possibilities like this:
a
|
a(bc) = b + a b
| \ /
c c
The point is that we can either attach the root of a to a vertex in
b, or a vertex in c. There are fewer possibilities when we form
a(bc):
a
|
(ab)c = b
|
c
so
a(bc) - (ab)c = a b
\ /
c
Now switch a and b in this equation! We get
b(ac) - (ba)c = b a
\ /
c
Our rooted trees are not planar, so the answer is really the same:
a b b a
\ / = \ /
c c
So, we have
a(bc) - (ab)c = b(ac) - (ba)c
and this is the definition of a pre-Lie algebra!
This calculation reveals the secret meaning of pre-Lie algebras. The secret is that pre-Lie algebras are all about attaching two things by connecting a special point of the first to an arbitary point of the second! Rooted trees are the universal example, so they give the free pre-Lie algebra on one generator.
This calculation also reveals that a pre-Lie algebra is really a vector space with a bilinear product whose "associator"
{a,b,c} = (ab)c - a(bc)
is symmetric in the last two variables.
Finally, let me tell you the third way to get pre-Lie algebras: from operads. I'll assume you know about linear operads, which I explained in "week282".
Suppose O is any linear operad. Let A be the free O-algebra on one generator. Then A becomes a pre-Lie algebra in a god-given way!
You should have seen this coming, since operads are related to trees. The details are explained here:
22) Frédéric Chapoton and Muriel Livernet, Pre-Lie algebras and the rooted trees operad, Int. Math. Res. Not. 2001 (2001), 395-408. Also available as arXiv:math/0002069.
The idea is that A is a lot like O, since we get elements of the free O-algebra on one generator by hitting that generator with operations in O. More precisely, we have
A = ⊕ On/Sn
Here On is the space of n-ary operations in O, which is acted on by the permutation group Sn. So, we can draw an element of A like this:
o o o
\ | /
-----
| a |
-----
|
o
where a is an n-ary operation in O, but we don't care how the
branches of this little tree are permuted.
We can multiply two guys like this by summing over all ways of attaching the output of one to an input of the other and composing them using our operad. And, thanks to the "secret meaning of pre-Lie algebras", this makes A into a pre-Lie algebra!
This is nice. But over dinner, James Dolan, Bill Schmitt and I came up with an even slicker construction which seems to give the same multiplication on A.
A is the free O-algebra on one generator, say x. So, for any element a in A, there's a unique O-algebra endomorphism
f(a): A → A
sending x to a. Note that f(x) is the identity. By the general philosophy that "an infinitesimal endomorphism is a derivation", the operator
(d/dt) f(x + ta)|t = 0
is a derivation of A.
(For certain familiar sorts of algebras, you may aready know what a derivation is. These are just special cases of a general concept of derivation for O-algebras. I leave it as an exercise to reinvent this general concept.)
Now, we can define a multiplication on A by
ab = (d/dt) f(x + ta)(b)|t = 0
And this is the same as the multiplication I just described. Can we use this slick description to more efficiently prove that A is a pre-Lie algebra? I don't know.
One last thing:
Any linear operad gives a pre-Lie algebra. But pre-Lie algebras are themselves algebras of a linear operad! This leads to curious self-referential situation, and a nice puzzle.
There's a linear operad whose algebras are pre-Lie algebras. As we have seen, for any linear operad O, the free O-algebra with one generator becomes a pre-Lie algebra. So: the free pre-Lie algebra on one generator becomes a pre-Lie algebra in this way. But of course it already is a pre-Lie algebra! Do these pre-Lie structures agree?
If you give up, you can find the answer here:
23) Dominique Manchon, A short survey on pre-Lie algebras, available at http://math.univ-bpclermont.fr/~manchon/biblio/ESI-prelie2009.pdf
But if you want to solve this puzzle on your own, it helps to think about what the operad for pre-Lie algebras looks like. Let's call it PL. It's not hard to guess what it looks like, given everything I've told you so far.
I've told you that the free pre-Lie algebra on one generator has a basis given by rooted trees. And I've told you a general fact: the free O-algebra on one generator is
⊕ On/Sn
So, taking O = PL, it should come as no surprise that PLn, the space of n-ary operations in PL, has a basis given by rooted trees with n vertices labelled by numbers 1 through n. Modding out by Sn just gets rid of those labels!
But how do you compose operations in PL?
Addendum: I thank Colin Backhurst, Tim van Beek, and James Stasheff for improvements. Eugene Lerman pointed out that this paper provides a nice introduction to the Hopf algebra of rooted trees:
24) Christian Brouder, Trees, renormalization and differential equations, Numerical Mathematics 44 (2004), 425-438. Also available at http://www-int.impmc.upmc.fr/~brouder/BIT.pdf
Let me quote:
Abstract. The Butcher group and its underlying Hopf algebra of rooted trees were originally formulated to describe Runge-Kutta methods in numerical analysis. In the past few years, these concepts turned out to have far-reaching applications in several areas of mathematics and physics: they were rediscovered in noncommutative geometry, they describe the combinatorics of renormalization in quantum field theory. The concept of Hopf algebra is introduced using a familiar example and the Hopf algebra of rooted trees is defined. Its role in Runge-Kutta methods, renormalization theory and noncommutative geometry is described.Introduction
This paper tells the story of a mathematical object that was created by John Butcher in 1972 and was rediscovered by Alain Connes, Henri Moscovici and Dirk Kreimer in 1998. Butcher wanted to set up a theory of Runge-Kutta methods in numerical analysis, Connes and Moscovici were working at an index theorem in noncommutative geometry, Kreimer was looking for the mathematical structure behind the renormalization method of quantum field theory, and all these people hit upon the same object: the Hopf algebra of rooted trees. The appearance of an object relevant to so widely different fields is not common. And the fact that a computer scientist discovered it 26 years in advance shows the power of inspiration provided by numerical analysis. Connes and Kreimer themselves noted: "We regard Butcher's work on the classification of numerical integration methods as an impressive example that concrete problem-oriented work can lead to far-reaching conceptual results".
Here are some examples, taken from Connes and Kreimer's paper, that illustrate the comultiplication in the Hopf algebra of rooted forests:
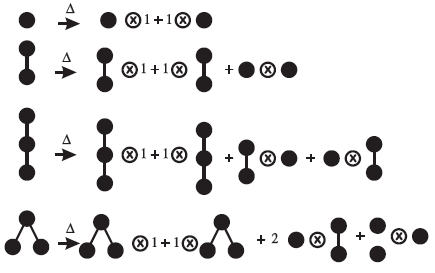
Here Δ stands for the comultiplication. But beware: these trees have their root on top - I hear that's how they grow in Europe. So, these pictures are upside-down compared to the description I gave earlier! Now to comultiply a rooted forest we slice it in lots of ways and form a sum of terms
(above) ⊗ (below)
For example, the terms in the last line of the picture come from these ways of slicing the given tree:

Here's another nice introduction to pre-Lie algebras and the Hopf algebra of rooted forests:
25) Frédéric Chapoton, Operadic point of view on the Hopf algebra of rooted trees, http://www-math.unice.fr/~patras/CargeseConference/ACQFT09_FredericCHAPOTON.pdf
But beware: he is using right pre-Lie algebras, where I was using left ones. So, his product obeys the law
[R(a), R(b)] = R([a,b])
where R(a) stands for right multiplication by a. Right pre-Lie algebras work just as well as left ones.
For more discussion, visit the n-Category Café.
I can learn only by teaching. - John Wheeler
© 2010 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|