Lecture 22 - Symmetric Monoidal Preorders

Last time we took our beloved preorders and combined them with another kind of mathematical gadget - monoids - to get "monoidal preorders". Preorders say when can get something from something else. Monoids let us combine things. Monoidal preorders let us do both!

This is a common trick in math: taking two mathematical structures and blending or "hybridizing" them to get a new one. It's good to think carefully about it:

A preorder is a set \(X\) with a relation \(\le\) that's reflexive and transitive.
A monoid is a set \(X\) where we can combine elements using an associative operation \(\otimes\), together with an element \(I\) that has no effect when we combine it with anything else: \(I \otimes x = x = x \otimes I\).

But to hybridize these, we don't just rudely slap them together. We want our \(\le\) relation to get along with our "combining" operation \(\otimes\)! So, we define a monoidal preorder to be a thing \( (X, \le, \otimes, I) \) such that \( (X,\le \) is a preorder, \( (X, \otimes, I) \) is a monoid, and also

[ x \le x' \textrm{ and } y \le y' \textrm{ imply } x \otimes y \le x' \otimes y' .]

This last condition is the magic pixie dust that makes monoidal preorders really interesting.

On the one hand this condition makes perfect sense: if you can get \(x\) from \(x'\) and \(y\) from \(y'\), you should be able to get \(x\) combined with \(y\) from \(x'\) combined with \(y'\).

But on the other hand, you might wonder if it's really "magic". Did finding this condition require a burst of inspiration? Or could there be some systematic way to have found it? Indeed there is!

Puzzle 66. What's another way to state this last condition using ideas we've already discussed? Hint: it's a property of the function \(\otimes: X \times X \to X\).

A good category theorist knows lots of systematical ways to find good definitions, which convert "magic" to "method".

A lot of the monoidal preorders will be talking about are "symmetric". This means that given \(x\) combined with \(y\), you can always get \(y\) combined with \(x\).

Definition. A monoidal preorder \( (X, \le, \otimes, I) \) is symmetric if

[ y \otimes x \le x \otimes y ]

for all \(x,y\in X\).

Since \(x\) and \(y\) are anything, we can switch their roles and conclude that

[ y \otimes x \le x \otimes y \textrm{ and } x \otimes y \le y \otimes x ]

for all \(x,y\) in a symmetric monoidal preorder. You might guess that this implies \(x \otimes y = y \otimes x\), but no! This will follow if our preorder is a poset, since a poset is a preorder where

[ a \le b \textrm{ and } b \le a \textrm{ implies } a = b .]

But it's not true in general:

Puzzle 67. A monoidal preorder is commutative if \(x \otimes y = y \otimes x\) for all \(x,y\). Find a symmetric monoidal preorder that is not commutative.

There are lots of great examples of symmetric monoidal preorders. For starters, many of your favorite number systems:

The set \(\mathbb{R}\) of real numbers with the usual \(\le\), the binary operation \(+: \mathbb{R} \times \mathbb{R} \to \mathbb{R} \) and the element \(0 \in \mathbb{R}\) is a symmetric monoidal preorder.
Same for the set \(\mathbb{Q}\) of rational numbers.
Same for the set \(\mathbb{Z}\) of integers.
Same for the set \(\mathbb{N}\) of natural numbers.

In fact, all these are commutative monoidal posets. But we've also seen some other examples in our discussion of chemistry and Petri nets in Lecture 19. For example, take this Petri net:

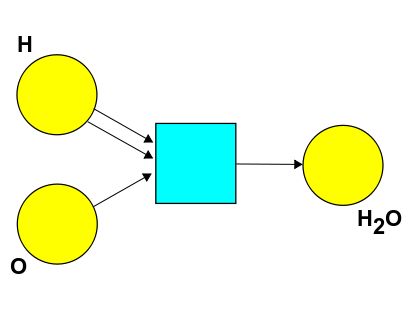
This describes the formation of water from hydrogen and oxygen atoms (in an idealized and unrealistic way - it's not really that simple). From this you can create a symmetric monoidal preorder where the elements are expressions like this:

[ a \text{H} + b \text{O} + c \text{H}_2\text{O} ]

where \(a,b,c\in \mathbb{N}\). Mathematical chemists call these complexes. There's an operation for combining complexes, called \(+\), and it's defined this way:

[ (a \text{H} + b \text{O} + c \text{H}_2\text{O} ) + (a' \text{H} + b' \text{O} + c' \text{H}_2\text{O} ) = (a+a') \text{H} + (b+b') \text{O} + (c+c') \text{H}_2\text{O} ]

This \(+\) operation is associative, and the element

[ 0 = 0 \text{H} + 0 \text{O} + 0 \text{H}_2\text{O} ]

has the property that \(0 + x = x = x + 0 \) for any complex. So, the set of complexes becomes a monoid. The only question is how we define \(\le\).

Puzzle 68. How should we define \(\le\) on the set of complexes to get a symmetric monoidal preorder, if the only nontrivial chemical reaction we want to describe is the one shown below?

Puzzle 69. Is this symmetric monoidal preorder a poset?

Puzzle 70. Suppose we also consider the reverse reaction:

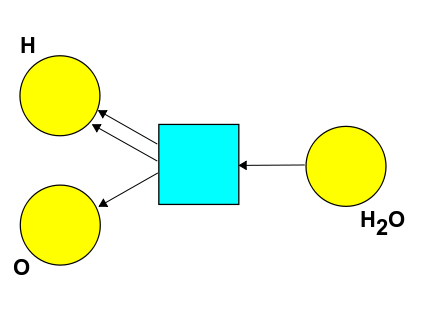
How should we change our definition of \(\le\) to get a new symmetric monoidal preorder? Is this a poset?

To read other lectures go here.