Lecture 36 - Categories from Graphs

Lecture 36 - Categories from Graphs

In Section 3.2.1 of Seven Sketches, Brendan Fong and David Spivak describe a nice way to get categories from graphs. It's very simple, yet important for building databases.

Here's the basic idea. Start with a graph, for example this:

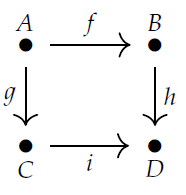
It has a bunch of "edges", like \(f,g,h,i\), going between "nodes" like \(A,B,C,D\). Then build a category where the objects are the nodes and the morphisms are the paths of edges. We compose morphisms by attaching one path onto the end of another.

For example \(f\) is a path of length 1 from \(A\) to \(B\), so it gives a morphism \(f: A \to B \). \(h\) is a path of length 1 from \(B\) to \(D\), so it gives a morphism \(g: B \to D\). We can compose these two morphisms and get \(h \circ f : A \to D\), which is a path of length 2 from \(A\) to \(D\).

There's also another morphism from \(A\) to \(D\), namely \(i \circ g : A \to D\).

In this example the longest paths have length 2, but in general a path could have any natural number as its length, including 0. Paths of length 0 are important because they give the identity morphisms in our category. For example, there's a path of length 0 from \(A\) to \(A\), which you can't see because it has no edges! It gives the identity morphisms \(1_A: A \to A\).

When we build a category from a graph this way, it's called the free category on that graph. And if we call the graph \(G\), we call the free category on that graph \(\mathbf{Free}(G)\).

I should warn you that different people mean different things by "graph", depending on:

But category theorists have a very specific thing in mind when we say "graph". We are very generous: we say yes to all these questions!

So, for example, we allow this graph:

This graph has just one edge. But the free category on this graph has infinitely many morphisms, namely [ 1_z : z \to z ] [ s : z \to z ] [ s \circ s : z \to z ] [ s \circ s \circ s : z \to z ] and so on. There's one morphism for each natural number. In fact, this is how category theorists often think about the natural numbers!

We also allow this graph:

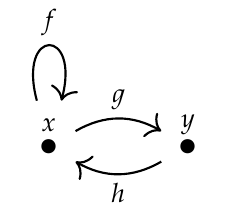
Puzzle 104. How many paths of length \(n\) go from \(x\) to \(x\) in this graph?

The answer is a famous sequence of numbers. So, you're getting a famous sequence from the free category on a graph!

It may sound complicated to let our graphs have so many features, but it's actually more complicated to disallow them. The category theorists' definition of graph is very simple:

Definition. A graph \(G\) is a set \(N\) of nodes, a set \(E\) of edges, a function \(s : E \to N\) assigning each edge its source, and a function \(t: E \to N\) assigning each edge its target.

You can visualize the source and target of an edge using this picture:

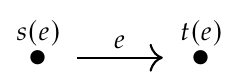
but remember: it's possible to have \(s(e) = t(e)\).

If you're a stickler for detail, you may also want to see the precise definition of a "path":

Definition. Given a graph, a path from a node \(x\) to a node \(y\) is a finite sequence of edges \((e_1, \dots, e_n)\) with

[ s(e_1) = x, \quad t(e_1) = s(e_2), \quad \dots, \quad t(e_{n-1}) = s(e_n), \quad t(e_n) = y. ]

Here \(n = 0, 1, 2, 3, \dots\) is called the length of the path.

Okay, I think that's enough for today! Next time we'll use this idea to think about databases. For now you should try these exercises, or at least look at other students' solutions:

Exercise 3. Show that \(\textbf{Free}(G)\) really is a category.

Exercise 4. Completely work out the set of morphisms between each pair of objects in the category called \(\textbf{3}\), which is

[ \textbf{Free}( [ v_1 \overset{f_1}{\rightarrow} v_2 \overset{f_2}{\rightarrow} v_3 ] ) .]

Exercise 5. The category \(\textbf{3}\) is an example of a general idea. For each natural number \(n\) there's a category \(\mathbf{n}\) that works the same way. Figure out what it is, and figure out the total number of morphisms in this category!

And here's a puzzle for people who love numbers. I'll admit it: I love numbers. But math is not only about numbers, so if you don't love them, don't worry: this puzzle is not important for this course, though it is part of a big subject in math:

Puzzle 105. It's been known since at least the fifth century BC that [ \sqrt 2 = 1 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \cfrac{1}{2 + \ddots\,}}}}} ] If we cut off this continued fraction we get these rational approximations to \(\sqrt{2}\): [ \frac11, \frac32, \frac75, \frac{17}{12}, \frac{41}{29}, \frac{99}{70}, \dots] where the denominator of the \(n\)th fraction in this list is called the Pell number \(P_n\) and the numerator is \(P_n + P_{n-1}\). Find a graph with two nodes \(x\) and \(y\) such that the number of paths of length \(n\) from \(x\) to \(y\) is the \(n\)th Pell number.

To read other lectures go here.

© 2018 John Baez