Lecture 68 - Feedback in Collaborative Design

Last time we began studying feedback in co-design diagrams. This led us into a fascinating topic which we'll explore more deeply today: cups and caps. Ultimately it leads to the subject of 'compact closed' categories, which Fong and Spivak introduce in Section 4.5.1. Covering this material adequately will take longer than the three weeks I'd intended to spend on each chapter, but I think it's worth it.

Last time we saw that for each preorder \(X\) there's a feasibility relation called the cup

[ \cup_X \colon X^{\text{op}} \times X \nrightarrow \textbf{1} ]

which we draw as follows:

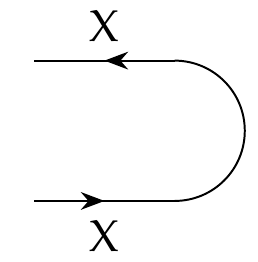
To define the cup, we remembered that feasibility relations \(X^{\text{op}} \times X \nrightarrow \textbf{1}\) are monotone functions \( (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \to \mathbf{Bool} \), and we defined \(\cup_X\) to be the composite

[ (X^{\text{op}} \times X)^\text{op} \times \textbf{1} \stackrel{\sim}{\to} (X^{\text{op}} \times X)^\text{op} \stackrel{\sim}{\to} (X^{\text{op}})^\text{op} \times X^{\text{op}} \stackrel{\sim}{\to} X \times X^{\text{op}} \stackrel{\sim}{\to} X^{\text{op}} \times X \stackrel{\text{hom}}{\to} \textbf{Bool} ]

where all the arrows with little squiggles over them are isomorphisms - most of them discussed in Puzzles 213-215. In short, the cup is the hom-functor \(\text{hom} \colon X^{\text{op}} \times X \to \mathbf{Bool}\) in disguise!

The cup's partner is called the cap

[ \cap_X \colon \textbf{1} \nrightarrow X \times X^{\text{op}} ]

and we draw it like this:

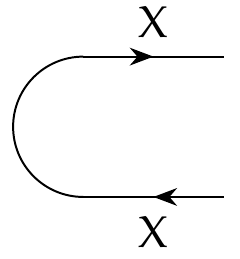
The cap is also the hom-functor in disguise! To define it, remember that feasibility relations \(\textbf{1} \nrightarrow X^{\text{op}} \times X\) are monotone functions \(\textbf{1}^{\text{op}} \times (X^{\text{op}} \times X) \). But \(\textbf{1}^{\text{op}} = \textbf{1}\), so we define the cap to be the compoiste

[ \textbf{1}^{\text{op}} \times (X^{\text{op}} \times X) = \textbf{1}\times (X^{\text{op}} \times X) \stackrel{\sim}{\to} X^{\text{op}} \times X \stackrel{\text{hom}}{\to} \textbf{Bool} . ]

One great thing about the cup and cap is that they let us treat the edges in our co-design diagrams as flexible wires. In particular, they obey the snake equations, also known as the zig-zag identities. These say that we can pull taut a zig-zag of wire.

The first snake equation says

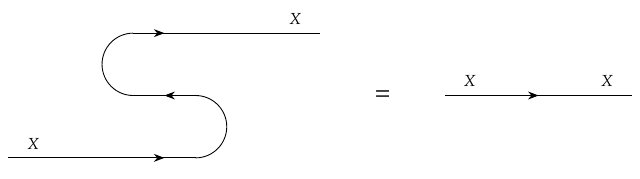
In other words,

[ (1_X \times \cup_X) (\cap_X \times 1_X) = 1_X .]

Please study the diagram and the corresponding equation very carefully to make sure you see how each part of one corresponds to a part of the other! And please ask questions if there's anything puzzling. It takes a while to get used to these things.

The second snake equation says

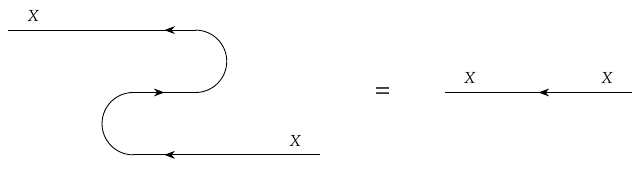
In other words,

[ (\cup_X \times 1_{X^{\text{op}}}) (1_{X^{\text{op}}} \times \cap_X) = 1_{X^{\text{op}}} .]

A great exercise, to make sure you understand what's going on, is to prove the snake equations. You just need to remember all the definition, use them to compute the left-hand side of the identity, and show it equals the much simpler right-hand side.

Puzzle 217. Prove the snake equations.

In fact some of you have already started doing this!

To read other lectures go here.