Leatherworking

Okay, this is a "just-for-fun" posting on braids. I had a mind-bending exploration of topology the other night with a friend that I'd like to recommend to all of you. Take a long thing piece of paper in it and cut two parallel long slits in it like so:

This represents the trivial braid on three strands. You can actually get nontrivial braids by "cheating" and grabbing the end marked $A$ (below) and sliding it through one of the slits -- say the top one, around the position marked $X$ (the exact position doesn't matter, of course), and then pulling it back to about its original position:

If you do this in the simplest possible way, you will get a braid in which two of the strands cross around each other twice, while the third strand is not tangled with the other two -- but all the strands have a 360 degree twist in them now!!

(So really we are working here not with braids but "framed braids," in which each strand has a certain twist to it. Framed braids also form a group which has the ordinary braid group as a quotient.)

Okay, here's your puzzle. Get your piece of paper to look like this as a braid -- with no strand having any twist in it:

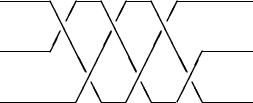
This sort of braid, where top and bottom strand take turns going over the middle strand, is the typical braid found in hairdos. Here however the exact number of crossings counts. Note two neat things about this braid. First, each strand winds up in its original position (top to top, middle to middle, bottom to bottom) - i.e. its image in the symmetric group is the identity. Second, if we get rid of any one strand the remaining two are unlinke (i.e. form a trivial braid on two strands). Thus it's a braid analog to the "Borromean rings" (three linked circles no pair of which are linked).

Anyway, getting your piece of paper to look like this without any cutting and pasting is a topological trick well-known to leather-workers, who can make seamless leather braids this way. My friend and I were unable to make this braid except using the following trick. Grab the strands near the left (as in the first picture) and braid them to look like the desired braid, ignoring the fact that near the right things are getting all screwed up. Now look at what you have at the right -- the inverse braid of the one you want (no surprise, since the whole braid is still the identity braid)! While preserving the left half, which is the way you want it, now use "cheating" moves on the right half (i.e., grab the right end and slip it through the slits) to kill off the unwanted junk (the inverse braid of the one you want). You can do it with three, or perhaps even just two, "cheating moves" -- if you're clever! You are now left with the desired braid as in the third picture!

Now there has got to be a more straightforward way of doing this! One should simply be able to create the desired braid by 2 or 3 cheating moves. Unfortunately my friend and I never succeeded. It's sort of like we knew how to differentiate but not how to integrate. But we learned some interesting topology in the process -- and that's what counts! So I strongly recommend that everyone make a 2-slitted strip of paper (leather would be better) and see what kinds of framed braids they can make. There is clearly an interesting sort of group lurking here: the subgroup of framed braids that can be generated by "cheating moves". I am sure that topologists have figured this stuff out already, but it's more fun to mess with it yourself in this case.

© 1992 John Baez
baez@math.removethis.ucr.andthis.edu

home