Charged Particles in a Magnetic Field

I've decided that the end of my previous article is just a bit too brief and enigmatic for those not up on their quantum mechanics. So I'll explain what happens to a charged particle in the plane when its in a magnetic field, and how one gets a noncommutative torus out of this situation. Then, since it's the holiday season, I'll let myself digress to discuss a particle on a sphere in a magnetic field.

First, let's set $\hbar = 1$. CLICK!

Suppose we have a particle on the plane -- with no magnetic field. Then in quantum mechanics the momenta in the $x$ and $y$ directions are given by the operators,

$$p_x = -i \partial/\partial x\quad{\rm and}\quad p_y = -i \partial/\partial y$$

respectively. These commute, becuase mixed partials commute.

Now let's turn on the magnetic field pointing perpendicular to the plane. Let's say our particle has charge = 1, and the field is B (of magnitude $B$). The curious fact about quantum theory is that (if we neglect the spin of the particle) the only effect of the magnetic field is to make us redefine the momentum operators to be

$$p_x = -i \partial/\partial x + A_x \quad {\rm and}\quad p_y = -i\partial/\partial y + A_y$$

where A, the vector potential, has $\mbox{\boldmath$\nabla\times$} {\bf A} = {\bf B}$. Now $p_x$ and $p_y$ don't commute, and in fact the commutator

$$p_x p_y - p_y p_x$$

is just $-iB$ ...as everyone should check for whom it isn't instantly, blindingly obvious. It's a pity that when I was first learning quantum mechanics the teacher didn't remark on how curious and charming this is: when there's a magnetic field around, the different components of the momentum no longer commute, and the amount by which they fail to commute is precisely the magnetic field! Recall that the meaning of momentum in quantum theory is that it's the generator of spatial translations. This means that if you grab your charged particle and move it first along the $x$ direction and then the $y$ direction:

the particle winds up in a different state than if you first go in the $y$ direction and then the $x$ direction:

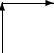
Another way of thinking of it is as follows: take your particle, move it counterclockwise (say) around a rectangle:

and it'll be back in the same place, but its wavefunction will not be the same as it was: it'll differ by a phase (multiplication by a complex number of unit magnitude). It's easy to calculate that if we call the particles wavefunction to start out with "$\psi$," and when we're done "$\phi$,"

$$\phi = e^{is} \psi$$

where $s$ is just the line integral of ${\bf A}\cdot d{\bf l}$ around the rectangle routes. By Stokes' theorem, $s$ is just the integral of $B$ over the rectangle!

If I had been told this, I might have absorbed it a bit more quickly when I was told in fancier language later on that the momentum operators $p_x$ and $p_y$ were components of a "connection" on a "complex line bundle," and that their commutator was the "curvature" of this connection, so that the magnetic field is really a curvature, and that the difference in phase obtained by taking two routes is called the "holonomy" of the connection. For that's the modern way of discussing this sort of thing.

Anyway, now suppose that the magnetic field strength is a constant $B$. Let $U$ denote the unitary operator corresponding to translation by a unit distance in the $x$ direction, and let $V$ be the unitary operator corresponding to a unit translation in the $y$ direction. Then by what I've said, we have

$$UV = qVU$$

where $q = e^{iB}$. Thus $U$ and $V$ satisfy the relations of a noncommutative torus.

More generally, if you move a charged particle counterclockwise around any loop, its phase changes by $e^{is}$, where $s$ is the integral of $B$ over the region enclosed by the loop. Note that the "counterclockwise" bit comes from using Stokes' theorem. (Also, an oppressive majority of right-handed people have enforced foolish "right-hand rules" ...don't you think it'd make more sense to call clockwise the positive orientation? Oh well.) If we go clockwise, the phase change is $e^{-is}$.

This still holds when our particle is not on a plane but on some other sort of two-dimensional surface, but there are some curious consequences.

Consider, for example, a particle on a sphere (for mathematicians, $S^2$), with a magnetic field applied that's normal to the sphere at each point. If we move the particle around a loop the phase change will equal the integral of the magnetic field over the region enclosed by the loop. But wait a minute! There are two different regions, the "inside" and the "outside" of the loop, which count as regions enclosed by the loop! (Just draw a circle on a sphere and look!) Who is to say which one we should use to calculate the phase change? There's only one way out: we had better get the same answer each way! That is, if we call the integral of the magnetic field over the region "inside" the loop $B_1$, and over the region "outside" the loop $B_2$, we must have

$$e^{iB_1} = e^{-iB_2}$$

Where'd that minus sign come from? Well, if the loop goes counterclockwise around one region, it goes clockwise around the other region, so one of them gets a minus sign. (Draw a circle on a sphere and look!) In any event, if we write $B = B_1 + B_2$ for the integral of the magnetic field over the whole sphere, the above equation gives

$$e^{iB} = 1$$

so $B$ must be an integer multiple of $2 \pi$!

This is an odd but true result, and it applies not only to the sphere but to any (compact, oriented) surface: we can only make sense of a charged quantum mechanical particle on such a surface in a magnetic field perpendicular to the surface if the integral of the magnetic field is a integer multiple of $2 \pi$.

This result too may be gussied up in fancy mathematical language. (And it's not just jargon, but crucial in understanding this problem more deeply.) The wavefunction of our charged particle on the sphere, or any other surface, is not really a function, but a section of a complex line bundle over the surface. Giving such a line bundle a connection, calculating the curvature, integrating the curvature over the surface, and dividing by $2 \pi$, we must get an integer! (Again, I'm assuming the surface is compact and oriented: e.g. a sphere, torus, or donut with more holes...) This integer is called the first Chern number $c_1$ of the line bundle. A deeper theorem says that given a surface we can cook up a line bundle with any desired $c_1$, and another theorem says that line bundles over surfaces are completely classified by their first Chern number.

Okay, now -- did you notice the following physical problem with what I did? Say we have a sphere in $R^3$, and a magnetic field perpendicular to the sphere, such that the integral over the sphere is $2 \pi n$. (As we saw above $n$ has to be an integer.) Unless $n=0$, this means that there is a net magnetic flux flowing in or out of the sphere -- which contradicts the fact that $\mbox{\boldmath$\nabla\cdot$} {\bf B} = 0$! I.e., Gauss' theorem says that the integral of the normal component of B over the sphere is 0, since $\mbox{\boldmath$\nabla\cdot$} {\bf B} = 0$.

Well, this didn't bother Dirac! In fact, he came up with all this stuff when he was studying magnetic monopoles! He considered the possibility that $\mbox{\boldmath$\nabla\cdot$} {\bf B}$ was nonzero in the vicinity of some monopole, but considered a big sphere around the monopole, assumed $\mbox{\boldmath$\nabla\cdot$} {\bf B} = 0$ in the vicinity of this big sphere, and used quantum mechanics to show (as above) that total magnetic charge inside the sphere must be an integer multiple of $2 \pi$! I've dropped all the units, but if you throw $\hbar$ and the electron charge back in correctly, you get a "quantum of magnetic charge".

There's another way around the problem, too, which mathematicians can tolerate, if not physicists: just say "I'm considering a particle in a magnetic field on some abstract $S^2$, not one sitting inside ${\bf R}^3$, so I don't need to worry about the ball `inside' my sphere."

Or, if you like, you can say, "How do you know there's not a wormhole inside my sphere, so that the B field can be pouring in from somewhere else?" In other words, "My sphere is a nontrivial 2-cycle in a 3-manifold, so it is possible for a closed 2-form (the magnetic field) to have nonzero integral over it." This is the basis for a suggestion by Wheeler, that charged particles are really the mouths of wormholes, and that actually the divergence of E and B are zero everywhere.

As you can see, weaseling out of this problem can take many interesting forms! That is, perhaps, the essence of mathematical physics. :-)

© 1992 John Baez
baez@math.removethis.ucr.andthis.edu

home