Anyons and Braids

In my previous post I was discussing the Conway polynomial. In the early 1980s, Vaughan Jones came up with a shockingly similar knot invariant. Interestingly, he arrived at it via von Neumann algebras, a kind of operator algebra invented by von Neumann to study the foundations of quantum physics (among other things). With the Jones polynomial and Conway polynomial around people immediately started searching for a generalization that would encompass both and soon a whole bunch of people found one. It's often called the HOMFLY polynomial these days after the initials of some (but not all) of its discoverers. This "polynomial" is really a Laurent polynomial in two variables, namely a polynomial in $x$, $x^{-1}$, and $z$. It may be calculated by the following rules:

Rule 1: If $K$ is the unknot (an unknotted circle), $G(K) = 1$. This is sort of a normalization rule.

Rule 2: Suppose $K$, $K'$, and $L$ are 3 knots (or links) differing at just one crossing (we're supposing them to be drawn as pictures in 2 dimensions).

At this crossing they look as follows:

$K$ looks like:

$K'$ looks like:

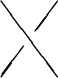
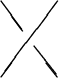
$L$ looks like:

(Again, all of them should have arrows pointing down, and any rotated version of this picture is fine too.)

Then we have the "skein relation" (here's where it's different from the Conway polynomial):

$$xG(K) - x^{-1}G(K') = zG(L) .$$

Nice and simple! (Though it's not at all trivial to prove its existence and uniqueness!) Note that the variable $x$ keeps track of handedness or what a physicist might call "parity" -- it's an easy exercise to show that if the knot $K^*$ is the mirror image of $K$ then

$$G(K^*)(x,z) = G(K)(x^{-1},z)$$

It's a pleasant exercise to use rules 1) and 2) to calculate this polynomial for the left-handed and right-handed trefoil knot and see that the answers are different.

Now the question becomes, what is this polynomial trying to tell us? Here I need a digression into the theory of braids, and, to keep the physicists interested, I'll begin with anyons.

We all know that particles come in two fundamentally different flavors: bosons and fermions. The argument for this is simple, well-known, and a bit misleading. It goes like this. Say we have a bunch of $n$ identical particles. Their state is described by a wave vector (a vector in a complex Hilbert space). We may permute the particles without really doing anything since they are identical, you can think of it as just permuting their "labels". Now in quantum mechanics two wave vectors which differ only by a phase (a scalar factor of unit modulus) describe the same physics. Thus we must have a representation of the symmetric group $S_n$ on the Hilbert space, and it must map any permutation to a scalar multiple of the identity. There are only 2 such representations (another charming exercise): the trivial representation and the one mapping each permutation to its sign. In the former case we say the particles are bosons, and in the latter, fermions.

This seems to be the case in reality. Interestingly, all the fundamental particles one might call "matter" are fermions (quarks and leptons), while all the particles one might call "force fields" are bosons (the photon, W, Z, and gluons). Here of course I am skirting the issue of the Higgs particle, that curious fudge factor. If the Japanese decide to pay for the superconducting supercollider we will see if the Higgs exists.

If one pays close attention to the argument, however, it's full of holes. First of all, why do we really need a representation of $S_n$ -- in quantum mechanics a projective representation is good enough! Secondly, if one considers representations where $S_n$ does not act as scalars but as an "internal symmetry group" one gets even more possibilities. These were investigated under the name of parastatistics. Anyway, one can come up with a better argument, the spin-statistics theorem, in relativistic quantum field theory, and that, together with the fact that parastatistics can be redescribed as fermions and bosons in disguise, seems to give a solid explanation for why all we see is bosons and fermions. (Though I couldn't say I'm very familiar myself with the whole story.)

Now for the catch: the spin-statistics theorem only holds for spacetimes of dimension 4 and up. You could just say "thank heavens! that just happens to apply to our universe!'' and leave it at that, or you could note that it's occaisionally possible to simulate universes of lower dimension. Take, for example, a thin 2-dimensional layer of stuff: this can act like a little 3-dimensional spacetime. Similarly, filaments can act like 2-dimensional universes. These days condensed matter theorists delight in the odd processes that occur in these contexts, and it was only a matter of time before someone noted that one can, at least in principle, arrange to get particles that are neither bosons or fermions. Wilczek is generally credited with taking the idea of these ``anyons'' seriously, though it had occured to others earlier.

Here's how it goes in its most primitive form. Say we have some tubes of magnetic flux moving around. (One can play with these flux tubes using superconductors, for example). As long as these tubes stay parallel the problem is essentially a 2-dimensional one: pick a plane perpendicular to the flux tubes and just pay attention to their intersection with that plane. Each tube intersects the plane in a spot which we will regard as a ``particle''. In each spot there is a B-field perpendicular to the plane, and going around each spot is an A-field whose curl is the B-field. If you like you can think of each spot as a ``vortex'' of the A-field. Now suppose -- and here I don't know if this has ever been experimentally achieved -- that each tube is electrically charged. In our planar picture then, we've got these ``particles'' which are charged, each also being a vortex of the A-field. Let's assume that all these particles are identical. Now let's see what happens when we interchange two of them. Recall that when you move a particle with charge $e$ through an A-field, its phase changes by

$$e^{i \theta}$$

where $\theta$ is the line integral of the A-field along the path traversed by the particle. Thus when we interchange two of our particles -- and here I mean you physically ``grab'' them and move them around each other so that they trade places! -- the wave vector of the system is changed by a phase. I'll let you calculate it. The point is, depending on the charge and the strength of the magnetic flux tube, one can arrange for this phase to be whatever one likes -- any complex number of magnitude one! If this number equals $1$ one has bosons, if it's $-1$ one has fermions, but otherwise one has anyons.

One can have fun playing with this idea. Many people have. Wilczek is a big proponent of an anyonic theory of high-temperature superconductivity, although recent experiments, demonstrating an apparent absense of spontaneous parity violation that one would expect in this theory, seem to rule it out. It's not 100% dead, though, and in my opinion it's so beautiful that someone should try to make a superconductor based on this principle just for the glory of it. Something that anyone who has followed me so far can have fun doing, is to see what sort of particle a bound state of anyons acts like. It's well-known that two fermions together act like a boson, two bosons act like a boson, and a boson and a fermion act like a fermion ...extend this to anyons.

A question for the real physicists out there: has anybody ever really made anyons and played with them yet?

Now anyons have a lot to do with braids because, as you may have noticed, I have covertly stopped thinking of the the operation of interchanging identical particles as an abstract ``switching'' -- modelled by the symmetric group -- and started thinking of it as moving one particle around another. If one draws the worldlines of some anyons as one moves them around each other this way, one has -- a braid! I.e., out with the symmetric group, in with the braid group!

The high-handed manner in which I've thrown out the symmetric group and started working with braid group statistics should disturb you, but again I can cite fancy mathematical physics papers which should allay your fears. A very nice one is "Local Quantum Theory and Braid Group Statistics" by Fröhlich and Gabbiani, which gives a proof of the generalized spin-statistics theorem that holds in 2 and 3 dimensions.

So now we see a close relation between quantum theory -- to be precise, "statistics'' in quantum theory -- and the braid group. Looking back at Kauffman's original insight into the relation of knots and quantum mechanics, it's not blindingly obvious what that has to do with this! Nonetheless it's all part of one story. (A story which I strongly feel is far from over.) More later.

© 1992 John Baez
baez@math.removethis.ucr.andthis.edu

home