
My working hypothesis is that living systems seem 'messy' to physicists because they operate at a higher level of abstraction than physicists are used to. That's what I'm trying to explore these days.
Back in 1963, Bill Lawvere had the idea that the process of assigning 'meaning' to expressions could be seen as a functor from one category to another. This idea has caught on in theoretical computer science: it's called functorial semantics.
The basic idea is that a program is a morphism in a category, and what it computes is a morphism in another category, and there's a functor from the first category to the second. Some programming languages like Haskell, Scheme and Scala have been designed to explicitly take advantage of this point of view.
What I want to to do is apply functorial semantics to biology. I expect that in biology there are many ways to view the 'meaning' of what's going on — there's no one best answer; instead, there are many different levels of abstraction at which we can usefully view things. Life somehow manages to exploit this.
This is hard to think about: biology is much more tricky than computer programming! So I've been starting with simpler things, like chemistry.
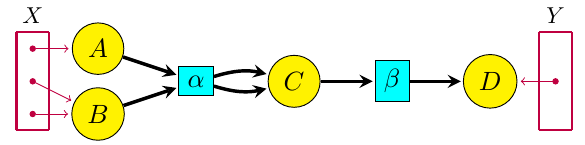
Blake Pollard and I have been working on open reaction networks: that is, networks of chemical reactions where some chemicals can flow in from an outside source, or flow out. The picture to keep in mind is shown above.
The yellow circles are different kinds of chemicals. The aqua boxes are different reactions. The purple dots in the sets X and Y are 'inputs' and 'outputs', where certain kinds of chemicals can flow in or out.
There's no serious difference between 'inputs' and 'outputs': chemical can flow in or out at any of these points. The only reason for segregating inputs and outputs is to make it easy to stick together two open reaction networks: we attach the outputs of the first to the inputs of the second.
This makes open reaction networks into the morphisms of a category. The main thing you do with morphisms is compose them, and here that means attaching the outputs of one open reaction network to the inputs of another.
Blake and I figured out how to first 'gray-box' an open reaction network, converting it into an open dynamical system, and then 'black-box' it, obtaining the relation between input and output flows and concentrations that holds in steady state. The first step extracts the dynamical behavior of an open reaction network; the second extracts its static behavior. And both these steps are functors between categories!
For a more detailed story about this, go here:

Forests in the east coast of the US are increasingly dangerous: there are more ticks that carry Lyme disease. My wife has a friend who got it after taking walks in the woods. But we can fight this disease — with foxes!
When you get Lyme disease, it starts with a circular rash near the tick bite. Then you may get chills and fever, a headache, fatigue, muscle and joint pain, and swollen glands. As the disease progresses you may experience severe fatigue, a stiff aching neck, and tingling or numbness in the arms and legs. Part of your face may become paralyzed. The most severe symptoms of Lyme disease may take weeks, months or years to appear. These can include severe headaches, painful arthritis, swelling of the joints, and problems with your heart and brain. Nasty!
Lyme disease is caused by bacteria that infect certain kinds of ticks. Why is this disease more common now?
I used to think it was the deer. With the lack of predators, and rules against hunting in many areas, deer populations have exploded, limited only by starvation when they eat everything they can find. The forests near my mother's home have been devastated by deer. The trees still look good, but there's no green undergrowth, so no new trees — because the deer eat everything. And deer carry the kind of ticks that cause Lyme disease.
But now I hear mice are also to blame. Mice also get infected by ticks. This year in New York there's been a big rise in ticks. And the cause is mice:
Everybody knows about Lyme disease. But experts say the Northern United States may be in for a bad tick season this summer, raising concerns about Lyme and other scary tick-borne diseases, including the Powassan virus, which causes encephalitis and can leave people with permanent neurological damage."This spring definitely seems worse than others I remember," said Dr. Catherine Wiley, chief of general pediatrics at Connecticut Children's Medical Center. "People are coming in from the yard with numerous ticks on them."
When we think of ticks, we tend to think of deer, but Richard S. Ostfeld, a senior scientist at the Cary Institute of Ecosystem Studies in Millbrook, N.Y., said it's really all about mice. He has been studying white-footed mouse population ecology for the past 25 years. Every four or five years, he said, there's a bumper acorn crop, so more mice survive the following winter, breed and reach what he called "mouse plague levels" in the summer.
These mice will be the main source of infection for the tiny larval ticks that hatch in August and can attach to many mammals and birds, which will try to groom them off. Mice "are just not fastidious groomers," Dr. Ostfeld said, so their ticks tend to survive. Those larval ticks then morph into the nymph stage and stay dormant through the following winter. And then, in late spring through early summer, the nymphs begin to feed. It's those nymphs, infected in the larval stage by mice, that transmit the infections to humans.
How can you control this? It turns out foxes do the job quite nicely! And they do it remarkably well: not just by eating mice, but by scaring mice so they spend more time in their burrows!
It is August, the month when a new generation of black-legged ticks that transmit Lyme and other diseases are hatching. On forest floors, suburban estates and urban parks, they are looking for their first blood meal. And very often, in the large swaths of North America and Europe where tick-borne disease is on the rise, they are feeding on the ubiquitous white-footed mice and other small mammals notorious for harboring pathogens that sicken humans.So, let's try to bring back foxes to the forests of the US! Besides, they're cool in their own right.But it doesn't have to be that way. A new study suggests that the rise in tick-borne disease may be tied to a dearth of traditional mouse predators, whose presence might otherwise send mice scurrying into their burrows. If mice were scarcer, larval ticks, which are always born uninfected, might feed on other mammals and bird species that do not carry germs harmful to humans. Or they could simply fail to find that first meal. Ticks need three meals to reproduce; humans are at risk of contracting diseases only from ticks that have previously fed on infected hosts.
For the study, Tim R. Hofmeester, then a graduate student at Wageningen University in the Netherlands and the lead researcher of the study, placed cameras in 20 plots across the Dutch countryside to measure the activity of foxes and stone martens, key predators of mice. Some were in protected areas, others were in places where foxes are heavily hunted.
Over two years, he also trapped hundreds of mice — and voles, another small mammal — in the same plots, counted how many ticks were on them, and tested the ticks for infection with Lyme and two other disease-causing bacteria. To capture additional ticks, he dragged a blanket across the ground.
In the plots where predator activity was higher, he found only 10 to 20 percent as many newly hatched ticks on the mice. Thus, there would be fewer ticks to pass along pathogens to next generation of mice. In the study, the density of infected "nymphs," as the adolescent ticks are called, was at 15 percent of levels in areas where foxes and stone martens were less active.
"The predators appear to break the cycle of infection," said Dr. Hofmeester, who earned his Ph.D. after the study.
Despite stuffing his pant legs into his socks and using permethrin, a tick repellent, he said he removed more than 100 ticks from his own body.
Interestingly, the predator activity in Dr. Hofmeester's plots did not decrease the density of the mouse population itself, as some ecologists had theorized it might. Instead, the lower rates of infected ticks, Dr. Hofmeester suggested in the paper, published in Proceedings of the Royal Society B, may be the result of small mammals curtailing their own movement when predators are around.
"This is the first paper to empirically show that predators are good for your health with respect to tick-borne pathogens," said Dr. Taal Levi, an ecologist at Oregon State University who was not involved in the study. "We've had the theory but this kind of field work is really hard and takes years." He also said of Dr. Hofmeester, "Wow, I have to send him an email."
Habitat fragmentation, hunting and the removal of larger predators like cougars may all figure into the dwindling of small mammal predators like foxes, weasels, fishers and martens, Dr. Levi said. If the study's results are borne out by more research, public health officials might be moved to try interventions like protecting foxes or factoring the habitat needs of particular predators into land-use decisions to foster their population size. Nothing else — like culling deer or spraying lawns with tick-killing pesticide — has worked so far to stem the incidence of tick-borne disease, which is spreading in the Midwestern United States, in parts of Canada and at higher altitudes across Europe.
"The takeaway is, we shouldn't underestimate the role predators can play in reducing Lyme disease risk," said Richard S. Ostfeld, a senior scientist at the Cary Institute of Ecosystem Studies, who originally speculated on the importance of small mammal predators in a 2004 paper. "Let's not discount these cryptic interactions that we don't see very often unless we put camera traps in the woods."
The first quote was from here:
The second is from here:

Back in the 1500's, people on long sea journeys navigated using the stars. They needed big tables of trig functions to do this!
These tables were made by astronomers. Those folks did thousands of calculations. Often they needed to multiply large numbers! That was tiring... but around 1580, they figured out a clever way to approximately multiply large numbers using tables of trig functions.
Here's an example:
Say you want to multiply 105 and 720. You do this:
Puzzle. Why is it close?
This wacky-sounding method has a wacky-sounding name: it's called prosthaphaeresis.
Tables of logarithms are easier. To multiply two numbers you just look up their logs, add them, and then look up the number whose log is that! But logs were invented only later, in 1614.
So for a while, prosthaphaeresis was the way to go!
And Napier, the guy who invented logs, did it after studying this earlier method.
It goes to show: a clunky way of doing something is often the first step toward something less clunky. You can't be slick right away!
For a nice answer to the puzzle, here's Chris Greene's comment on my G+ post:
So, let's call our original numbers \(x\) and \(y\). And let's reduce both of them by a scale factor \(s\) to get them in the range \((0,1)\). Then $$ x/s = \cos \theta_1 $$ $$ y/s = \cos \theta_2 $$ $$ xy/s^2 = \cos \theta_1 \cos \theta_2 $$ $$ xy = s^2 \cos \theta_1 \cos \theta_2 $$ So if we evaluate \( \cos \theta_1 \cos\theta_2 \) (using whatever magical method we desire) and multiply it by \(s^2\) we're good. (Of mild interest, we can actually scale the numbers by different amounts and nothing changes.) Noting that $$ \cos \theta = \frac{1}{2} (e^{i \theta} + e^{- i \theta}) $$ we can get $$ \begin{array}{ccl} \cos \theta_1 \cos \theta_2 &=& \displaystyle{ \frac{1}{4} (e^{i \theta_1} + e^{- i \theta_1})(e^{i \theta_2} + e^{- i \theta_2})} \\ \\ &=& \displaystyle{ \frac{1}{4} (e^{i (\theta_1 + \theta_2)} + e^{i (\theta_1 - \theta_2)} + e^{i (-\theta_1 + \theta_2)} + e^{i (-\theta_1 - \theta_2)})} \\ \\ &=& \displaystyle{ \frac{1}{4} (e^{i (\theta_1 + \theta_2)} + e^{-i(\theta_1 + \theta_2}) + \frac{1}{4} (e^{i (\theta_1 - \theta_2)} + e^{-i(\theta_1 - \theta_2)}) } \\ \\ &=& \displaystyle{ \frac{1}{2} (\cos(\theta_1 + \theta_2) + \cos(\theta_1 - \theta_2)) } \end{array} $$ The average of the complementary cosines! Of course, Napier took one look at that and said "That's insanely complicated! You don't need all those complex numbers and averaging! eᶿ is all you need! It works the exact same way, and none of this averaging the sum and and difference of angles nonsense!"cough
Well perhaps that was a slightly anachronistic approach. Most likely, some bright person noticed (without the aid of 18th century complex math) that
$$ \begin{array}{ccc} \cos (\theta_1 + \theta_2) &=& \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 \\ \\ \cos (\theta_1 - \theta_2) &=& \cos \theta_1 \cos \theta_2 + \sin \theta_1 \sin \theta_2 \end{array} $$ and added them together and saw that $$ 2 \cos \theta_1 \cos \theta_1 = \cos(\theta_1 + \theta_2) + \cos(\theta_1 - \theta_2) $$ thus obtaining $$ \cos \theta_1 \cos \theta_1 = \displaystyle{ \frac{1}{2} (\cos(\theta_1 + \theta_2) + \cos(\theta_1 - \theta_2)) } $$