

What happens if a black hole moves at the speed of light?
Well, an ordinary black hole can't, because only things with no mass can move at the speed of light. If a heavy thing zips past you, its gravity will yank at you for a short time. The faster it goes, the stronger this effect will be. The yank will last for a shorter time — but its total effect on you will be bigger. If the thing moved at the speed of light, this effect would be infinite. That makes no sense.
But we can do this. Take lighter and lighter black holes and make them move faster and faster, closer to the speed of light. In the limit we have a massless black hole moving at the speed of light! And it's not nothing — like a photon, which is also massless and moving at the speed of light, it has energy and momentum.
We can't do this in the lab — not yet, anyway. But we can work it out mathematically. We get a solution of Einstein's equations — the equations that describe gravity. This solution has a wonderful name: it's called the Aichelburg–Sexl ultraboost.
When something moves near the speed of light, it actually gets thinner - this is called a Lorentz contraction. So, the Aichelburg–Sexl ultraboost is a pulse of gravity that's infinitely thin, moving at the speed of light, strong near the center and weaker far away.
We can also do this trick with a spinning black hole. We get a solution of Einstein's equations that describes the gravitational field of a spinning massless particle.
Okay, that was the fun part for ordinary people. Now comes the math. In spacetime without any gravity messing things up, distances and times are measured by the Minkowski metric: $$ -dt^2 + dx^2 + dy^2 + dz^2 $$ We can write this down using other coordinates, like $$ u = \frac{x + t}{\sqrt{2}} $$ and $$ v = \frac{x - t}{\sqrt{2}} $$ in units where the speed of light is 1. These coordinates are called lightcone coordinates. They're nice because the surface \(u = 0\) is a plane moving forwards at the speed of light — just right for what we want. We get $$ -dt^2 + dx^2 + dy^2 + dz^2 = 2 du dv + dy^2 + dz^2 $$ Using polar coordinates in the \(yz\) plane, so that \(r^2 = y^2 + z^2\), this becomes $$ 2 du dv + dr^2 + r^2 d\theta^2 $$ If we now include a black hole moving at the speed of light, we get an extra term, and get the formula I showed above: $$ ds^2 = -8 m \delta(u) \log r du^2 + 2 du dv + dr^2 + r^2 d\theta^2 $$
The interesting thing is the first term. This describes a shock wave moving at the speed of light, which becomes infinitely strong at the center of the black hole! For more, see:
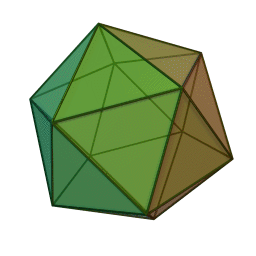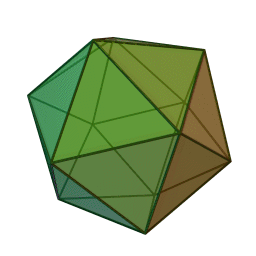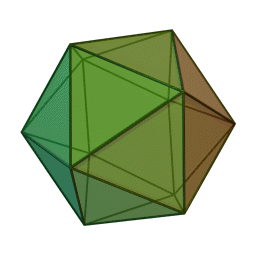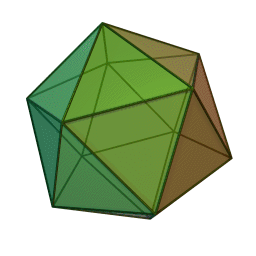
My latest quest is to find a really simple, clear way to get \(\mathrm{E}_8\) from the icosahedron. These are two of my favorite things, and they're connected.
The icosahedron is a Platonic solid with 120 = 1 × 2 × 3 × 4 × 5 symmetries. Just for fun, the picture here shows a 'stellated' icosahedron with sharper points. But it has all the same symmetries, and that's all that matters to me now.
\(\mathrm{E}_8\) is an 8-dimensional lattice: a periodic pattern of points in 8 dimensions. This pattern gives the densest way to pack spheres in 8 dimensions: center a sphere at each lattice point, and make them big enough to just touch each other. Each sphere touches 240 others. That's the maximum possible in 8 dimensions. And in fact, if you pack spheres in 8 dimensions and get each to touch 240 others, you've got \(\mathrm{E}_8\). This pattern shows up all over math, in cool and mysterious ways.
\(\mathrm{E}_8\) has two little brothers. If you take a well-chosen slice of \(\mathrm{E}_8\) you get a lattice called \(\mathrm{E}_8\). This gives the densest known way to pack spheres in 7 dimensions. Similarly, if you take the right slice of \(\mathrm{E}_8\) you get a lattice called \(\mathrm{E}_6\), which gives the densest known way to pack spheres in 6 dimensions.
The McKay correspondence is a way to get \(\mathrm{E}_6\), \(\mathrm{E}_8\) and \(\mathrm{E}_8\) from the tetrahedron, the octahedron and the icosahedron! This is one of nature's true marvels. It's yet more evidence that
There are actually several versions of the McKay correspondence. I'm interested in one called the 'geometric' McKay correspondence. Experts already understand it, but I want to bring it down to earth a bit... and I want to go for the jugular and focus on the icosahedron and \(\mathrm{E}_8\).
My plan is to look at the space of all ways you can place an icosahedron of any size centered at the origin in 3d space. This space is 4 dimensional, since it takes 3 numbers to say how the icosahedron is rotated, and 1 more to say its size. And this 4-dimensional space has a singularity where the icosahedron shrinks down to zero size!
It reminds me ever so slightly of the Big Bang, where we have a 4-dimensional spacetime with a singularity where the universe shrinks down to zero size (roughly speaking). But this is just a cute analogy, the sort science journalists use to attract and confuse readers. The lazy readers only look at the headline, and come away with weird ideas. Don't be one of them.
The serious business here is seeing how \(\mathrm{E}_8\) is lurking in the space of all possible icosahedra centered at the origin. Where is it?
It's sitting right at the singularity!
How? How is it sitting there, you ask?
I could tell you, but then I'd have to...
On second thought, I'll tell you here:
However, you'll need to know some math to follow this. The basic idea is that if you 'smooth out' or 'resolve' the singularity, it gets replaced by 8 spheres that intersect in a pattern governed by \(\mathrm{E}_8\).
This is just the first part of a series, since there's a lot I still
need to figure out! I want to see very concretely how these 8 spheres
show up. I'm hoping some math friends of mine will help me. With luck,
if we figure enough out, I can write a more polished article about it.
July 17, 2017
This movie shows right circularly polarized light. If you take your right hand, make a fist, and point your thumb in the direction the light is moving, the electric field will rotate in the direction your fingers are curling. There's also left circularly polarized light, where the electric field turns around in the other direction.
All this stuff can be figured out mathematically by solving the vacuum Maxwell equations, which describe light with no matter around.
But where can you see circularly polarized light in nature?
Albert Michelson found some back in 1911!
You may know this guy: he won the Nobel prize with Robert Morley for discovering that light moves past you at the same speed no matter how you're moving. But he also discovered something else. Light reflected from a certain kind of beetle called a golden scarab tends to be left circularly polarized! The reason was discovered much later: at the microscopic level, the shells of these beetles are made of spiral-shaped molecules!
Light from certain firefly larvae is also circularly polarized, but nobody knows why yet.
And sometimes starlight is circularly polarized... slightly. It's actually a messy mix of different kinds of light. Sometimes it's 'linearly' polarized — the electric field wiggles back and forth rather than round and round. This is because it scatters from elongated interstellar dust grains whose long axes tend to be oriented at right angles to the galactic magnetic field. But these grains spin rapidly, with their rotation axis along the magnetic field. This winds up creating a bit of circular polarization. The effect is tiny but measurable.
I was going to talk more about the math of circularly polarized light, but I got distracted. I wanted to explain how the polarization of light involves complex numbers. This is easier to talk about using quantum mechanics. To describe a photon with a certain energy in a certain direction, we need to use two complex numbers! A photon like $$ (1, 0) $$ is linearly polarized in one direction: say, its electric field wiggles back and forth. A photon like $$ (0, 1) $$ is linearly polarized in the other direction: say, its electric field wiggles up and down. So, a photon like $$ (1, 1) $$ would be linearly polarized in a diagonal way. But less obviously, a photon like $$ (1, i) $$ is right circularly polarized, and one like $$ (1, -i) $$ is left circularly polarized.
How did the complex numbers get into the game? We use them in quantum mechanics, but polarization of light is also there in the vacuum Maxwell equations, which were known before quantum mechanics. So the complex numbers should be lurking in the vacuum Maxwell equations!
They are. Mathematically, photons are solutions of the vacuum Maxwell equations. While these solutions involve two real vector fields, the electric and magnetic field, the space of solutions is a complex Hilbert space. To multiply a solution by \(i\) you multiply its positive-frequency part by \(i\) and its negative-frequency part by \(-i\).
In short: to fully understand light bouncing off a scarab beetle, you need to understand how the complex numbers are lurking in Maxwell's equations. The universe is cool. Let's be kind to our planet, so our civilization can stick around long enough to learn more. We're just getting started!
For more, try these:
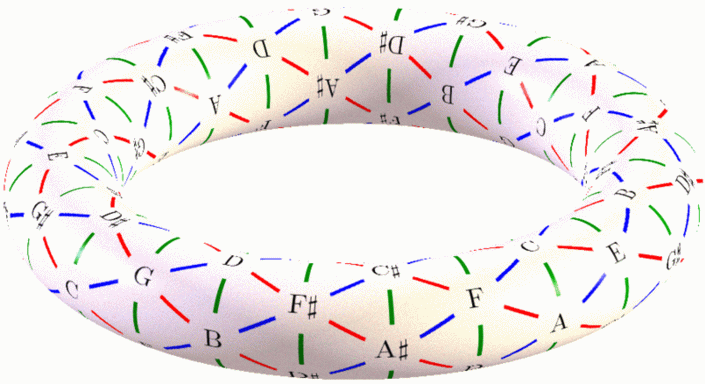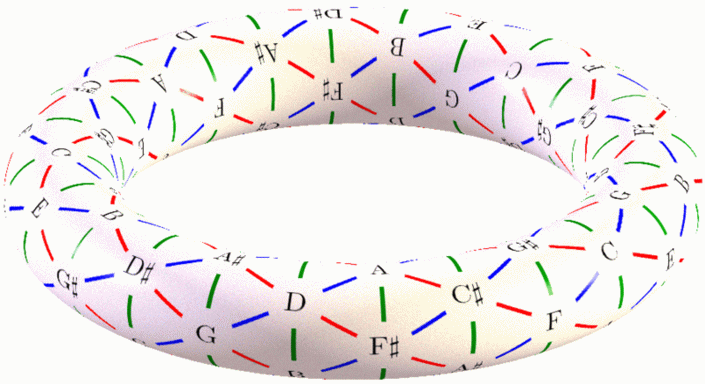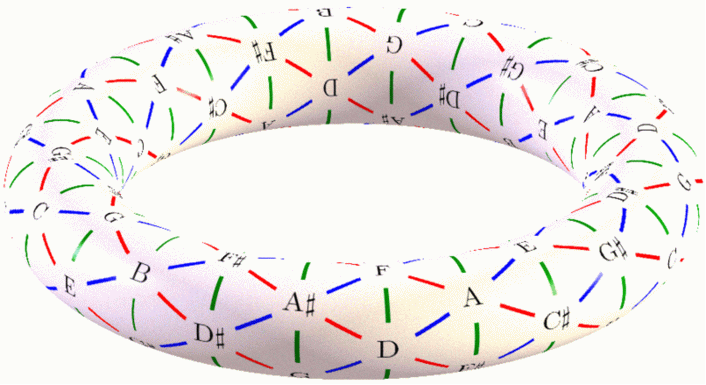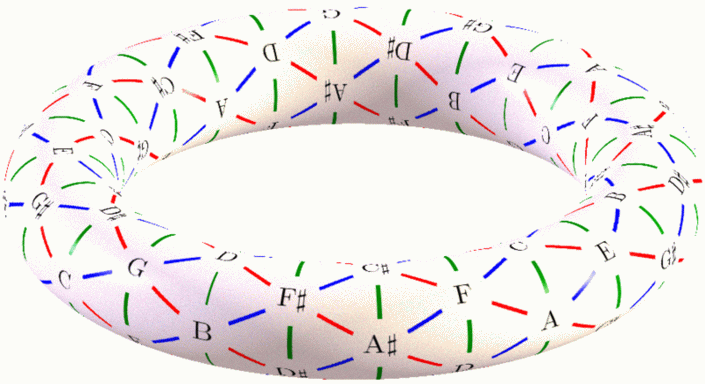
The geometry of music revealed! The red lines connect notes that are a major third apart. The green lines connect notes that are a minor third apart. The blue lines connect notes that are a perfect fifth apart.
Each triangle is a chord with three notes, called a triad. These are the most basic chords in Western music. There are two kinds:
A major triad sounds happy. The major triads are the triangles whose edges go red-green-blue as you go around clockwise.
A minor triad sounds sad. The minor triads are the triangles whose edges go green-red-blue as you go around clockwise.
This pattern is called a tone net, and this one was created by David W. Bulger. There's a lot more to say about it, and you can read more in this Wikipedia article: