Caucher Birkar was one of four Fields medalists this year:
So I read a bit about Birkar's work....
He's studying 'algebraic varieties', which are roughly curves, surfaces and higher-dimensional shapes described by polynomial equations. It's an old subject. In the 1800s people realized it's easier to study solutions with complex numbers, not just real numbers.
For example, above you can see the real points in an algebraic variety called Kummer's quartic surface — but there's a lot more going on with the complex solutions, and ultimately they make everything simpler, not more 'complex'.
It's also easier to study algebraic varieties if you add 'points at infinity'. For example, then all pairs of lines on the plane intersect — perhaps at infinity, like railroad tracks in perspective. This idea is called projective geometry.
Combining these ideas, 'complex projective space' is a nice framework for studying algebraic varieties. In this framework a circle, ellipse, parabola and hyperbola are all just different views of the same curve!
Nice and simple. So we can become more ambitious! We can try to classify all algebraic varieties. This sounds insane: classifying all possible curves, surfaces, and higher-dimensional things that you can describe with polynomials? Weird things like the Escudero nonic surface here, drawn here by Abdelaziz Merzouk?
So we have to be clever. First, we have to view algebraic varieties through very blurry glasses, so tons of them count as 'the same'. Not just circles and hyperbolas! We have to use 'birational equivalence', so the red and black curves here count as the same:
Very roughly speaking, two algebraic varieties are birationally equivalent if they're the same except on a very small set; this lets us eliminate singularities like the point where the red curve crossses itself.
Classifying algebraic varieties up to birational equivalence gets harder as their dimension goes up. Curves are all birationally equivalent. Surfaces come in 10 families, thanks to the Enriques–Kodaira classification.
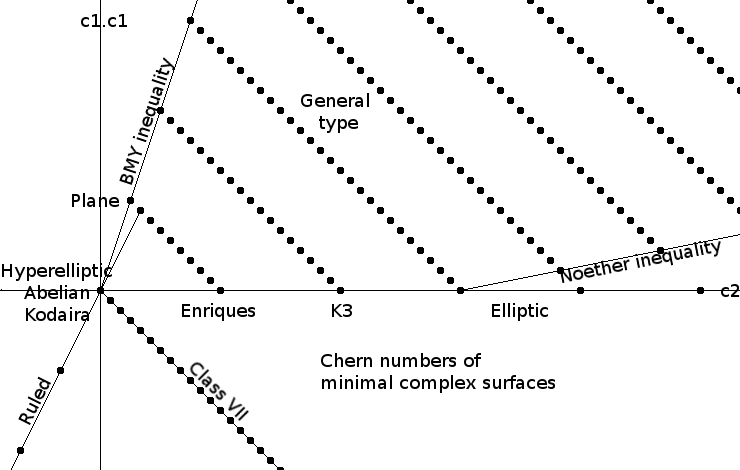
But in higher dimensions things get harder. Starting around 1980, the 'minimal model program' sought to find the 'simplest possible' algebraic variety that's birationally equivalent to whichever one you name:
It succeeded in 3 dimensions, thanks largely to the work of Mori:
He made progress on 'Fano varieties'. But what are those?
A smooth complex variety is Fano iff it admits a Kähler metric of positive Ricci curvature. Calabi-Yau varieties, famous from string theory, are 'Ricci flat', and most varieties are negatively curved. This rough 3-fold classification shows up all over math!
So very roughly, Caucher Birkar is contributing to a grand program to
classify all shapes described by polynomials... with a focus on
'positively curved' ones. But the technical details are way over my
head... and he's also done other things.
August 4, 2018
If you want to learn some cool physics, check out Bertolotti's
Physics
Factlets on Twitter.
August 5, 2018
The basic laws of arithmetic, like \(a \times (b + c) = a\times b + a \times c\), are secretly laws of set theory. But they apply not only to sets, but to many other structures!
Emily Riehl explained this in Eugenia Cheng's recent "Categories for All" session at a meeting of the Mathematical Association of America. Check out her slides:
The defining property of the product \(A \times B\) is that a function from any set \(X\) to \(A+B\) is the same as a function from \(X\) to \(A\) together with a function from \(X\) to \(B\).
The defining property of \(\mathrm{Fun}(A,B)\) is that a function from any set \(X\) to \(\mathrm{Fun}(A,B)\) is the same as a function from \(A \times X\) to \(B\). This change of viewpoint is called currying, and Riehl uses it twice in her proof.
She calls the defining property of \(+\) 'pairing', and she uses that twice too. I would call this copairing, but she wisely decided that sounds too technical.
Her proof actually never uses the defining property of \(\times\), which I would call pairing.
Her argument works for any category that has the necessary properties!
For example, the category of graphs. But it's nice to see that
lurking inside grade-school arithmetic there is an introduction to
category theory.
August 6, 2018
Nobody knows if there are infinitely many twin primes: primes
that are 2 apart. But Viggo Brun proved
the sum of the reciprocals of the twin primes converges.
Of course, if there were finitely many twin primes,
this sum would be rational. However, in theory, it could still be rational
even if there are infinitely many twin primes!
Now someone has conjectured a formula for this sum, which is called Brun's constant, \(B_2\).
The formula involves Catalan's constant \(G\): the alternating sum of reciprocals of odd squares. Nobody knows if this constant is irrational, though I bet it is.
The formula also involves the Ramanujan–Soldner constant \(\mu\). If you integrate the reciprocal of \(\ln(x)\) from 0 to this constant, you get zero.
Marcin Lesniak recently conjectured a formula relating Brun's constant to Catalan's constant and the Ramanujan–Soldner constant.
My guess: it's false. The discrepancy in the 12th decimal place is
not necessarily a problem, since the current best estimate of Brun's
constant uses an extrapolation: it's not necessarily a lower bound.
But the formula feels "too good to be true": we don't have any reason
to expect such a formula, since twin primes are even more hard to
understand than plain old primes. For example, they don't seem to be
connected to Dirichlet series the way plain old primes are.
August 11, 2018
Yesterday we arrived in Singapore. We've been visiting here for 9 years now!
Everything is instantly familiar, like waking up out of a dream. Someone at
the local market asked us if we come here when it's cold where we live.
We said no, we come here to escape the heat! (It's been over 100° F
almost every day for the last week in Riverside.)
In case you're wondering about the funny new format of some posts,
it's that I've moved from Google+ to Twitter. I found that people
like reading series of tweets where I explain math and physics. So
I'm copying some of these to my diary.
August 12, 2018
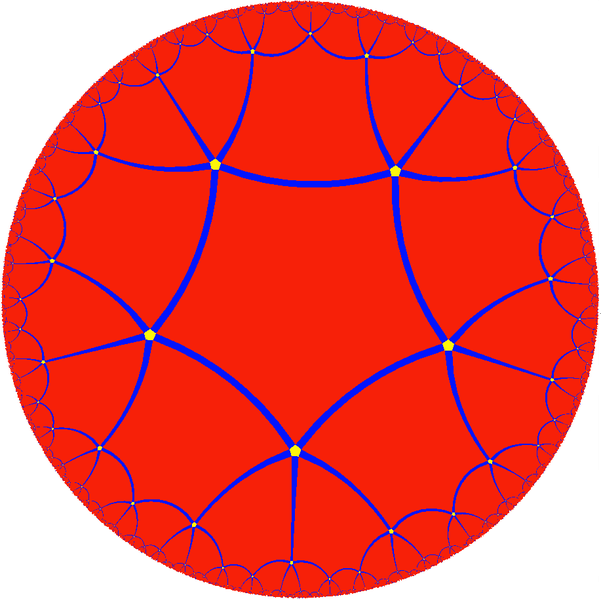
The number 5 is more exotic than all the natural numbers that come
before. So, take the hyperbolic plane and tile it with pentagons, 5
meeting at each vertex. This is the {5,5}
tiling. Very fiveish! We should be able to have fun with this.
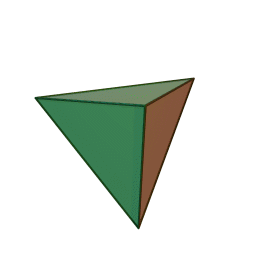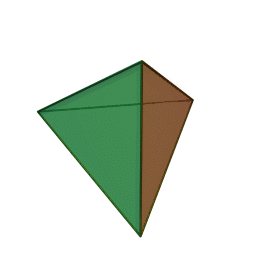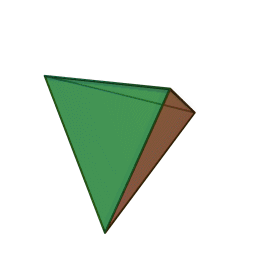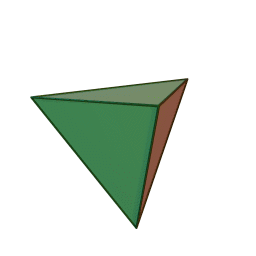
The {3,3} tiling of the sphere gives the tetrahedron, with 3 triangles meeting at each vertex:
The {4,4} tiling of the plane has 4 squares meeting at each vertex:
I could talk all day about these, but we're going straight for the jugular and doing {5,5}.
The {5,5} tiling has a big symmetry group. If we mod out by some of these symmetries we get a surface tiled by just 12 pentagons, with 5 meeting at each vertex.
Amazingly, we can almost embed this surface in 3d space while preserving most of its symmetries. The result is the great dodecahedron, drawn here using Robert Webb's Stella software:
The great dodecahedron has 12 vertices, 30 edges and 12 faces, which are pentagons that cross through each other. Now $$ 12 - 30 + 12 = -6 = 2 - 2g $$ with \(g = 4\), so it's really a surface of genus 4. That is, a 4-holed torus!
This picture is by Brokk:
The dual of the great dodecahedron is the small stellated dodecahedron:
The great mathematician Felix Klein showed that the Riemann surface coming from the small stellated dodecahedron can also be described by 3 equations in 5 complex variables:
$$ z_1 + z_2 + z_3 + z_4 + z_5 = 0 $$ $$ z_1^2 + z_2^2 + z_3^2 + z_4^2 + z_5^2 = 0 $$ $$ z_1^3 + z_2^3 + z_3^3 + z_4^3 + z_5^3 = 0 $$
They're homogeneous so they describe a complex curve in \(\mathbb{C}\mathrm{P}^4 \). It's a 4-holed torus. I prefer to understand it using the great dodecahedron: this aproach is equivalent, but simpler. What we're doing is giving the 4-holed torus the same conformal structure as if we give the interior of each pentagon in the great dodecahedron the metric it gets from its immersion in \(\mathbb{R}^3\). Angles are only distorted at the pentagon's vertices (not their edges).
There are many possible conformal structures on a 4-holed torus, but the one we get this way is the most symmetrical of all! Its symmetry group is \(\mathrm{S}_5\) the group of permutations of the 5 variables \(z_1 , \dots , z_5\).
See how fiveish it all is?
This amazing complex curve of genus 4 is also the set of ordered 5-tuples of complex numbers \( (z_1, \dots, z_5)\), modulo rescaling, that are roots of some quintic of the form \(z^5 + pz + q = 0 \), where \(p\) and \(q\) are arbitrary complex numbers. You can see a sketch of the proof, and references, in my blog article on this stuff:
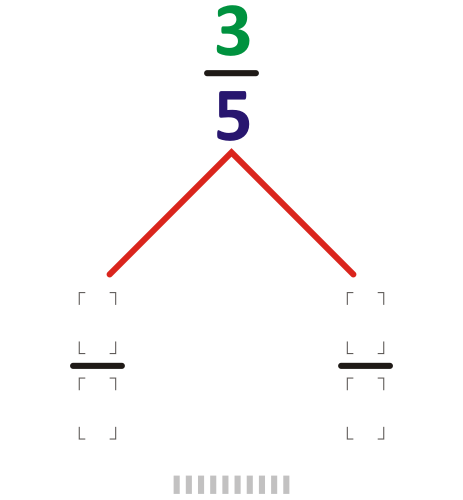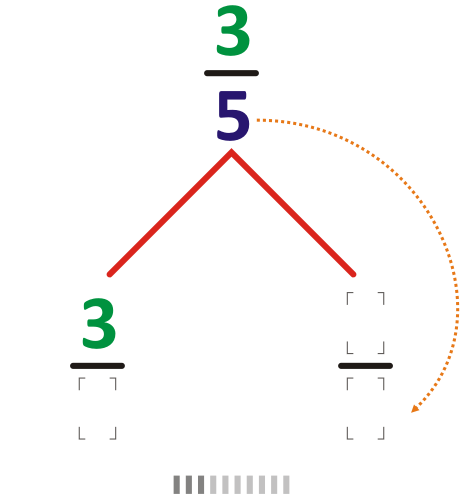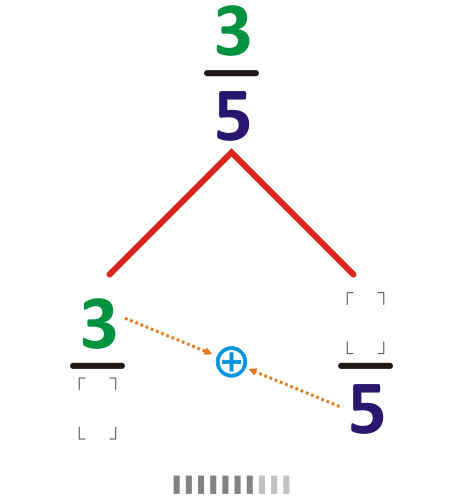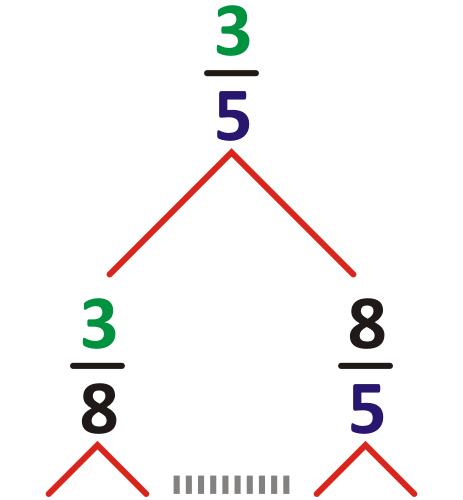
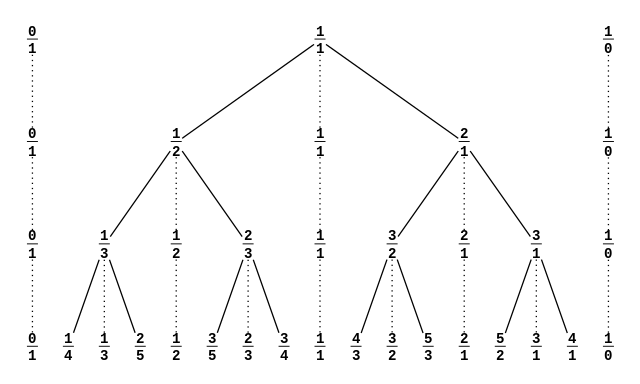
It's vaguely similar to the Calkin–Wilf tree:
This tree contains all the positive rational numbers — and each shows up just once! Can you spot the Fibonacci numbers? Can you see the pattern that's being used to get all the numbers in this tree?
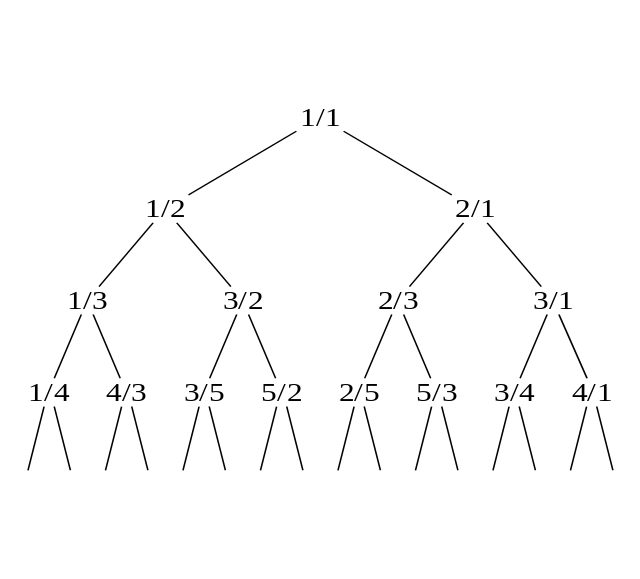
The Calkin–Wilf tree starts with \(1/1\).
If \(a/b\) is any fraction in the tree, then \(a/(a + b)\) is below and to the left. \((a + b)/b\) is below and to the right. Amazingly, each positive rational shows up just once, in lowest terms!
You can see why Fibonacci numbers show up! But the Calkin–Wilf tree also gives a nice way to list all positive rational numbers....
If you follow this spiral through the Calkin–Wilf tree, you'll meet each positive rational number exactly once, so you can list them all: $$ 1/1, \; 1/2,\; 2/1,\; 1/3,\; 3/2,\; 2/3,\; 3/1,\; 1/4,\; 4/3, \; 3/5, \; 5/2, \; 2/5, \; 5/3, \; 3/4,\dots $$
Amazingly, there's also recursive formula for this sequence! If you can't guess that recursive formula, you can look it up on Wikipedia. That's where I got all this great information... and all these nice pictures:
But how closely is all this connected to what Kepler was doing?
Here's what he wrote here (translated from the Latin):
I. The harmonic divisions of a single string are seven in number, not more.II. The expansion of the numbers which are characteristic of divisions occurs in the following manner. To being with, the whole is expressed in the form of a fraction, that is to say with unity above as numerator, and unity below for denominator. Then each number separately is put as numerator, and the sum of the two is put as denominator in each case. Hence from any given fraction two branches arise, until from the sum occurs the number which indicates an unconstructible figure.
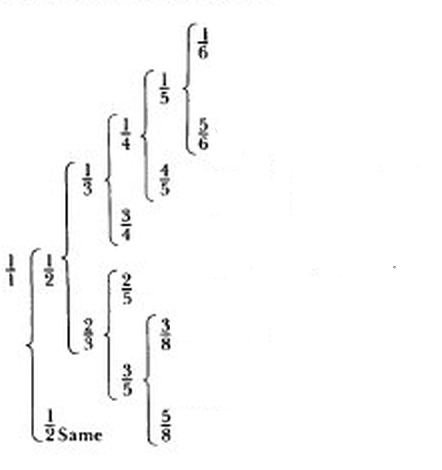
I believe 'unconstructible figure' alludes to a regular polygon that can't be constructed by ruler and compass: note that the 3,4,5,6 and 8-sided polygons can be so constructed, but not the 7, 9, 11, or 13-sided ones, which would come next. He shows these as well in his chart:
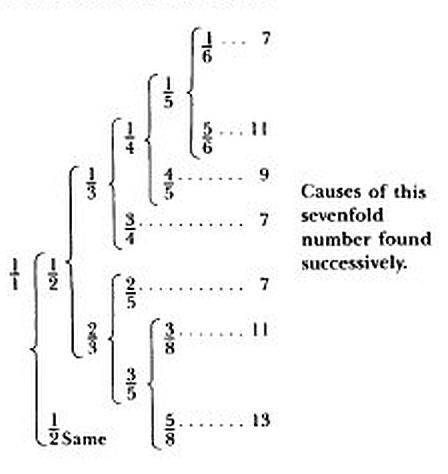
I believe he was trying to find the ratios of frequencies that appear in a a major scale, because of the remark that "the harmonic divisions of a single string are seven in number", and also the remarks that follow the above passage:
I found these seven divisions of the string first with hearing as a guide, in other words the same number as there are harmonies not greater than a single diapason. After that I dug out the causes both of the individual divisions and of the number of the total, not without toil, from the deepest fountains of geometry. Let the diligent reader read what I wrote about these divisions 22 years ago in The Secret of the Universe, Chapter XII.
So, he didn't want the tree to go on forever, even though it could.
He wanted to cut it off to avoid ratios involving 7, 9, 11, 13 or
more complicated numbers. And he did this by invoking the nonconstructibility
of these regular polygons — a fact that was apparently known even back
then, though not proved until later.
August 16, 2018
You can use quaternions to understand electrons!
Or: you can use electrons to understand quaternions!
Hamilton invented the formula for quaternion multiplication long before people knew quantum mechanics. But it describes what happens when you rotate an electron.
Usually people describe the spin of an electron using a pair of complex numbers... or in other words, 4 real numbers. But we can package the same information in a single quaternion: $$ a + bi + cj + dk $$ where \( a,b,c,d\) are real numbers and \(i,j,k\) are square roots of \(-1\).
When you rotate the electron 180° around the \(x\) axis, you multiply its quaternion by \(i\).
So when you rotate it 360°, it doesn't come back to where it was! Instead, since \(i^2 = -1\), it gets multiplied by \(-1\).
You have to rotate it 720° to get it back to where it was, like this contraption here:
But wait — what does it even mean to say the electron gets multiplied by \(-1\) if we rotate it 360°?
Shoot an electron through a double slit. It goes through both slits, and it's probability of hitting any point on the screen behind the slit forms an interference pattern. Make a machine that rotates the electron 360 degrees when it goes through the left slit. This changes the pattern: where the waves added up, they now subtract.
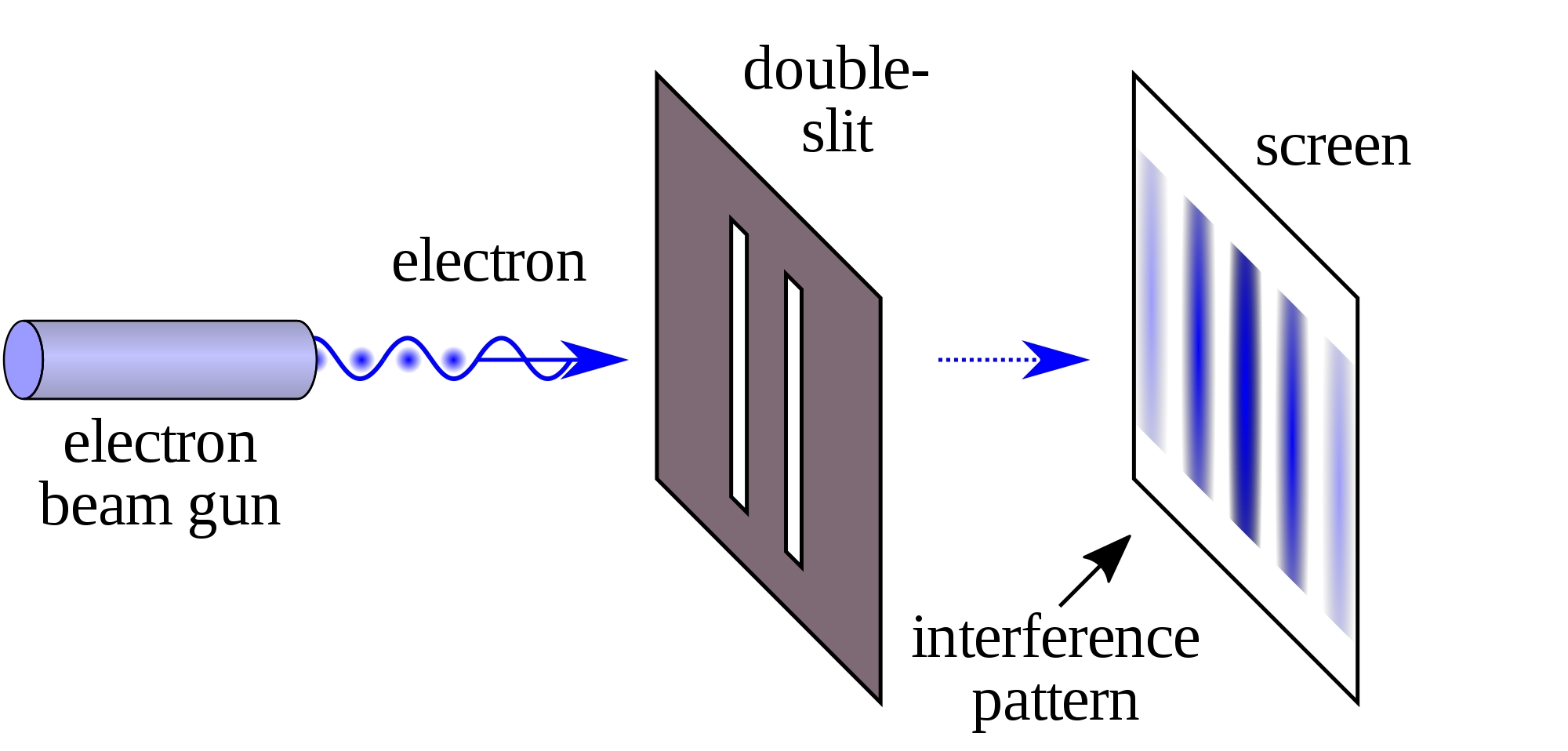
With work you can show experimentally that rotating an electron 360° around any axis multiplies it by \(-1\).
So, if we say that rotating it 180° around the \(x,y,\) or \(z\) axes multiplies it by \(i, j,\) or \(k\) respectively, then we conclude $$ i^2 = j^2 = k^2 = -1. $$ It's also true that rotating an electron 180° around the \(x\) axis, then the \(y) axis, and then the \(z\) axis multiplies it by \(-1\). This gives $$ ijk = -1 $$ In fact we get the whole quaternion multiplication table this way!
So: quaternions are built into physics.
Number theory is a great source of problems that are easy to state, hard to solve.
For experts, though, the fun comes from big ideas — often connected to other branches of math!
Artin's conjecture sounds cute when you say it's about repeating decimals:
Let's assume the coin is fair and — the hard part — each number \(1, 2, \dots, N\) has an equal chance of being chosen.
The answer is the purple curve here:
