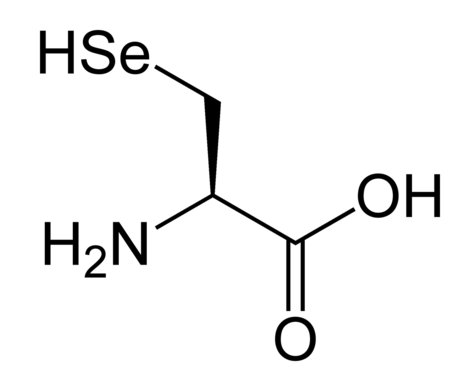
If you eat too much selenium, your breath smells like garlic and your hair falls out. But to stay healthy, you need about 15 milligrams in your body. That's because you use an amino acid called selenocysteine, shown above.
How does your DNA code for selenocysteine?
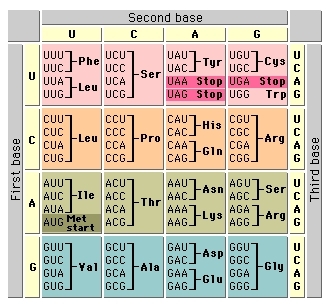
The ATCG base pairs in your DNA get translated to AUCG in RNA.
RNA has 64 different 'codons' - three-letter groups that code for amino acids, shown here:
How does your genome say when UGA means "selenocysteine" instead of "stop here"? It uses a selenocysteine insertion sequence — a bunch of RNA that looks like this:
In bacteria, this sequence comes shortly after the UGA. For eukaryotes like us, it's more complicated: the selenocysteine insertion sequence occurs in the 'three prime untranslated region' of a piece of RNA, or 3'UTR for short. This region does not code for amino acids! Instead, it contains instructions that affect how the rest of the RNA is interpreted.

I just figured out a neat analogy between classical mechanics and probability theory. I don't know a good name for the ??? concept here. But I know how the math works, so I just need to do more calculations to better understand this concept. This is a fun place to be.

Luckily, there's an exquisitely precise analogy between classical mechanics and thermodynamics. So I can pop over to thermodynamics, and think about how that is analogous to probability theory. This works better, since they both have a concept of entropy.
I explain how this works here:
But here's the key formula: it turns out the analogue of momentum in probability theory is $$ p_i = \frac{\partial S(q)}{\partial q_i} $$ where \(q = (q_1, \dots, q_n)\) is a probability distribution and $$ \displaystyle{ S(q) = - \sum_{i=1}^n q_i \ln(q_i) }$$ is its Shannon entropy. So, the 'momentum' \(p_i\) says how fast entropy increases as you increase \(q_i\).
You can think of this as analogous to pressure. Just as a gas 'wants'
to expand, a probability distribution 'wants' to flatten out to
increase its entropy — and the quantity
$$ p_i = \frac{\partial S(q)}{\partial q_i} $$
says how eagerly it wants the probability \(q_i\) to increase.
August 8

Thanks to Abel Jansma and Toby Bartels, I figured out what is to momentum as probability is to position. It's called 'surprisal' — a concept familiar in information theory. Surprisal is the logarithm of 1/probability.
I explain why here:
Then, after a bunch of calculations involving surprisal, I delve into the analogy between classical mechanics, thermodynamics and probability theory.
Unify! Unify! Unify! That's my motto these days.
We tend to treat the different frameworks for physics as different
things: classical mechanics, quantum mechanics, statistical mechanics,
classical thermodynamics. We know how they're
connected physically — but they haven't been unified as
much as they could be.
August 9, 2021
Here is Karen Cook's review in Early Music America:
Pierre de Manchicourt (c.1510–1564) was one of the most famous composers of his day. Born in French-speaking Flanders, he was a choirboy in nearby Arras by the age of 15, and by his mid-30s he was maître de chapelle at Tournai Cathedral. On the cusp of his 40th birthday, he became master of the chapel of Philip II of Spain, likely holding this position until his death a mere five years later.His network of associations reads like a Who’s-Who of the 16th-century musical elite. Through the immense patronage of the arts at the hands (or, rather, wallet) of Archbishop Granvelle, he was connected with well-known musicians such as Claudin de Sermisy and Tielman Susato. He would have worked alongside the likes of Jacob Clemens non Papa and Nicolas Gombert while under Philip II, and most of his works were published by Pierre Attaingnant, including a book of motets exclusively by Manchicourt. But by the end of the century, he was largely forgotten.
Unfortunately, even today Manchicourt remains a lesser-known name. In fact, this recording is the world premiere of his Missa Reges terrae, the only work on the album written during Manchicourt’s tenure with Philip II. The other five motets featured here were all composed well beforehand.
The Choir of St. Luke in the Fields has taken the rather refreshing approach of presenting the Mass in toto, instead of interspersing the other motets in between its movements. The recording starts with the source motet for the Mass, "Reges terrae," before continuing into the Mass itself. The motets "Caro mea," "Ne reminiscaris," "Vidi speciosam," and "Regina caeli," round out the disc.
The result is a solid, even enchanting album. The beautiful open-fifth head motive of "Reges terrae" is repeated at the start of every movement of the Mass, and each time it is just slightly spine-tingling. The ensemble is beautifully blended; each independent voice part is clearly heard, allowing the imitative motives to weave seamlessly into one another and creating that sense of constant forward motion Manchicourt cultivated. The "Benedictus," with its reduced forces, in this respect, is a tiny gem. It is clear that the Mass is the heart of the recording, both figuratively and literally, and is a much-needed addition to our discography of Renaissance music.
Yet I find the motets to be some of the most impressive polyphony I have heard recently. The central and closing cadences of "Vidi speciosum" are handled superbly, "Caro mea" is outstanding, and the slower tempo and crunchy dissonances of "Ne reminiscaris" are simply stunning. The gorgeous concluding Alleluia of "Regina caeli" is a moving end to a moving disc.
There is little to criticize here, though I would suggest that the portrayal of Philip II’s chapel and his relationship to music in the liner notes be taken with a grain of salt; the interested listener would do well to read some of Michael Noone’s or Luis Robledo’s work in tandem. Historical quibbles aside, I would be delighted to see the choir tackle the rest of Manchicourt’s music, for not only is a complete discography sorely needed, the ensemble also does his work justice.
Some snakes have hinged fangs that fold out when they bite! Like the Gaboon viper, with fangs almost 4 centimeters long. It only bites if you bother it a lot, but then it strikes fast &mdash and its venom is easily fatal.
Wikipedia writes, of the Gaboon viper:
It is best to avoid handling them in most circumstances.Understatement! Apparently they are very calm and docile... most of the time.
I thank Kam-Yung Soh for pointing out this nice article on the evolution of fangs in venomous snakes.

Wednesday: "Look, there's a bobcat on our fence! It's so cool living right next to a park!"
Today: walking out barefoot to pick some mint, I hear a rattlesnake
and see it three feet away. Yikes! Okay, cool, I'll just go inside.
August 20, 2021
I like it when apparent 'coincidences' are related. For example,
this surprising equation
$$ e^{\pi \sqrt{163}} = 262,537,412,640,768,743.99999999999925 \dots $$
is connected to a strange fact discovered by Euler:
$$ n^2 + n + 41 $$
is prime for \(n = 0, 1, 2, 3, \dots, 39\). The secret connection relies
on this fact:
$$ 4 \times 41 - 1 = 163. $$
On April Fool's Day in 1975, Martin Gardner claimed that \(e^{\pi \sqrt{163}}\) is an integer, and that this fact was predicted by Ramanujan. Like many other readers I ran to my calculator to check it — and yes, it seemed true! But it's not really an integer: it's just amazingly close to an integer.
This near-integer property of \(e^{\pi \sqrt{163}}\) relies on some deep number theory: 163 is a 'Heegner number'.
In general, \(e^{\pi \sqrt{n}}\) is close to an integer when \(n\) is a large Heegner number. But there aren't many Heegner numbers — and 163 is the largest! Here's how the four largest ones work:
$$ \begin{array}{ccl} e^{\pi \sqrt{19}} &\approx& 12^3(3^2-1)^3+744-0.22\\ e^{\pi \sqrt{43}} &\approx& 12^3(9^2-1)^3+744-0.00022\\ e^{\pi \sqrt{67}} &\approx& 12^3(21^2-1)^3+744-0.0000013\\ e^{\pi \sqrt{163}} &\approx& 12^3(231^2-1)^3+744-0.00000000000075 \end{array} $$ On the other hand, the polynomial \(n^2 + n + p\) gives a string of primes when \(4p-1\) is a Heegner number. Taking \(4p-1\) to be the biggest Heegner number, \(163\), gives the longest string of primes. So we should use \(p = 41\).
For the next-best case, take \(4p - 1 = 67\). That gives \(p = 17\). See how many primes you can get of the form \(n^2 + n + 17\). I'll get you started: $$ \begin{array}{ccl} 0^2 + 0 + 17 &=& 17 \\ 1^2 + 1 + 17 &=& 19 \\ 2^2 + 2 + 17 &=& 23 \\ \end{array} $$
This is all plenty of fun. But what's a Heegner number, and why does all this stuff work? For this we'll do a shallow dive into number theory. (I hate it when people say "deep dive" — usually when it's not.)
\(\mathbb{Q}[\sqrt{-n}]\) is the set of complex numbers of the form $$ a + b \sqrt{-n} $$ with \(a,b\) rational. \(\mathbb{Q}[\sqrt{-n}]\) is a field: it's closed under \(+, -, \times\) and \(\div\) (but don't divide by zero).
When \(n\) is Heegner number, this field has a cool property. Let me explain it.
We can define algebraic integers in any field: they're elements of that field that are roots of polynomials with integer coefficients and with leading term just \(x^n\). For the field of rational numbers, they're just the usual integers.
The idea of algebraic integers lets us generalize integers, prime numbers and so on to other fields! So, we can take a field like \(\mathbb{Q}[\sqrt{-n}]\) and ask if the algebraic integers in there have unique prime factorizations, like ordinary integers do.
Algebraic integers in \(\mathbb{Q}[\sqrt{-n}]\) have unique prime factorization for only nine choices of \(n\):
These, by definition, are the Heegner numbers. They have amazing properties, which explain the weird stuff I told you earlier.
For example, an important function called the j-invariant equals an integer at \((1 + \sqrt{-163})/2\) because 163 is a Heegner number. Using this together with a formula for the j-invariant, you can show that \(e^{\pi\sqrt{163}}\) equals an integer plus a tiny correction.
But how does 163 being a Heegner number make $$ n^2 + n + 41 $$ be prime for \(n = 0\) to \(n = 39\)?
This is a bit harder to explain. Check out this MathOverflow question, and the first answer:

The first answer to this question is detailed, but impossible to understand
unless you know about 'split', 'ramified' and 'inert' primes.
August 21, 2021

Condensed matter physics is amazing.
This paper published in Science says when an electron enters a certain kind of 'quantum spin liquid', its charge and spin and fermion statistics can get stripped off... leaving a ghostly residue.
What's really going on here?
What's going on is that different states of matter can wiggle in ways that act like particles of different kinds, called quasiparticles. In a quantum spin liquid we can have 'chargons' with only charge, 'spinons' with only spin, etc.
There's no such thing as an electron without charge and spin, but when an electron hits the edge of a material called a quantum spin liquid, it excites a wave in this material that behaves like a particle without charge and spin. So it seems like the electron leaves its charge and spin behind as it enters this substance.
But it can get complicated. A thin film containing quantum spin liquid can have different kinds of edges — and electrons entering from these edges will do different things!

Our trip went like this:
The drive to Louisville was a bit tough due to three different afternoon thunderstorms. We had fun having dinner with the mathematician Jack Morava and his wife in Charlottesville on the night before our final short drive, but going to our hotel afterwards we got stuck in an another thunderstorm, made worse by the fact that it was pitch black. So, I feel I've left the Land of Fire and entered the Land of Flood.
(Then came Hurricane Ida.)
August 31, 2021
Lisa and I are now living in the first floor of a nice house in the Center
for Hellenic Studies. Some other family lives on the second floor.
There are about five such houses, and also a building called the
'Stoa', which has one-room apartments. All these are full of visiting
fellows who showed up at the start of September. There's also a main
building where the fellows have offices, and where they eat. Due to
coronavirus restrictions I haven't actually seen any of these people
in person yet, and while Lisa will have lunch with them three times a
week, I won't — due to coronavirus restrictions. I plan to
spend that time walking around DC.
The cushy surroundings are courtesy of Harvard, who runs the Center for Hellenic Studies. I don't know how they got this spread of land in the first place. It's in the embassy district: behind us there's the Danish embassy, down the street there's the Italian embassy (which is huge - Italian diplomats must really have it made), and across the road there's the embassy of Sri Lanka. Behind the Danish embassy there's a large forest, the Dumbarton Oaks Park, that we can get to by following some paths. We got lost there on our first hike. I plan to get to know it well.
A bit to the north there's the Naval Observatory, which is where the vice president lives... so every day at 8 am we hear a loud version of The Star Spangled Banner! I guess it's good: it means that Kamala Harris can't sleep after 8.

But the biggest surprise is that a house across the street from us is owned by the Clintons! Apparently Hillary used it as the base for her 2016 campaign. So we are in a ridiculously fancy neighborhood.