
Why are logic and topology so deeply related?
Perhaps because we visualize a 'field of possibilities' as a kind of space. Not just a set, but a space with a topology, since some possibilities are closer to each other than others.
The idea that propositions should remain true if we change the state of affairs very slightly makes us treat them as open subsets of a topological space.
There are a few different topologies on the 2-element set \(\{T,F\}\), drawn here by Tai-Danae Bradley:
The Sierpiński space has two points, \(T\) and \(F\), and three open sets:
$$ \{ \}, \quad \{T\}, \quad \{T,F\}. $$
There's a very interesting asymmetry between 'true' and 'false' here. \(\{T\}\) being open means we're treating truths as stable under small perturbations.
Here's the coolest fact about the Sierpiński space \(\{T,F\}\). Open sets in any topological space X correspond to continuous maps \(f\colon X \to \{T,F\}\). Given the function \(f\), the corresponding open set is $$ \{x\in X : f(x) = T\}. $$ For details, read this blog post:
Perhaps we need a new word: logotopy!
'Topos' means 'place', and 'logos' means 'word'. In topology, we use
words to talk about places. In logotopy, we use places to talk about
words.
September 2, 2021
Yesterday Hurricane Ida ripped through DC very early in the morning,
and a 25-foot tree near the bedroom fell over, snapped off near the
base. If it were bigger and fell in a different direction, I could
have died. Not very likely, but imaginable — and if it happened,
you could say I died from climate change.
September 3, 2021
Yesterday Lisa took me out to dinner at a fancy little French
restaurant quite close to here. It was a very nice evening. We
decided not to walk through the Dumbarton Oaks Park because it's not
open at night and I was afraid she might trip over a tree root or
rock. She'd tripped on the sidewalk twice that day; she'd caught
herself, but I didn't like it. So, instead, we took a much more
roundabout route on sidewalks. I held her hand in the dark patches.
We'd almost made it home — I wasn't holding her hand at this
point — when she tripped and fell completely flat on her face.
At first she was just lying face down, with blood leaking onto the
sidewalk.... it was pretty scary. She could barely talk because she
had the wind knocked out of her. But she got her breath and it turned
out she didn't have a concussion, she hadn't lost any teeth, she
didn't have a detached retina (which she'd had once before), she
didn't have any broken bones... just a bunch of cuts and bruises.
Pretty scary. It goes to show how things can go awry so easily.
September 4, 2021
The black curve here is called the 'twisted cubic'. It consists of points \(x,x^2,x^3\). It's drawn here as the intersection of two surfaces: $$ y = x^2 \textrm{ and } z = x^3 $$ It's a nice example of many ideas in algebraic geometry. Let's talk about one!
I just described the twisted cubic using a map from the ordinary line to 3d space sending \(x\) to \(x,x^2,x^3)\). But in algebraic geometry we like the 'projective line'. This has coordinates \([x,y]\), where \([x,y]\) and \([cx,cy]\) describe the same point if \(c \ne 0\), and we don't allow both \(x\) and \(y\) to be zero. So let's use the projective line instead!
Similarly, projective 3d space has coordinates \([a,b,c,d]\), where multiplying all these coordinates by the same nonzero number doesn't change the point.
The twisted cubic is the image of this map from the projective line to projective 3d space: $$ [x,y] \mapsto [y^3,y^2 x ,y x^2, x^3] $$ To get back to our original twisted cubic in ordinary 3d space, just set \(y = 1\): $$ [x,1] \mapsto [1,x,x^2,x^3] $$ This is a fancy way of saying what I said in my first tweet! But the projective twisted cubic also has an extra point, where \(y = 0\). It's like a 'point at infinity'.
You can generalize this idea. Take any list of \(k\) variables and map it to the list of all monomials of degree \(n\) in those variables. You get a map called the 'Veronese map'. The twisted cubic is the case \(k = 2\), \(n = 3\).
In this blog post I described how to use the twisted cubic to get the spin-3/2 particle by 'triplicating' the spin-1/2 particle, using geometric quantization:
This application is what first got me interested in the twisted cubic. But this is just a special case of using the Veronese map to 'clone' a classical system, creating a new system that consists of \(n\) identical copies of that system, all in the same state. Then you can quantize that system, and get something interesting! I explain this here:
The picture of the twisted cubic came from here:
You can read more about the twisted cubic here:

Given a list of points in the plane, you can draw a 'Bézier curve'. This gif shows how. Each green dot moves linearly from one point to the next, each blue dot moves linearly from one green dot to the next... etc.
Surprisingly, this is connected to probability theory! To get the Bézier curve from a list of points, take a linear combination of these points where the coefficient of the \(i\)th point is this function of \(t\): the probability of getting \(i\) heads when you flip \(n\) coins that each have probability \(t\) of landing heads up!

The coefficients are called 'Bernstein polynomials', and their definition using probability theory makes it obvious that they sum to 1. Also that they're \(\ge 0\) when \(0 \le t \le 1\). Also that the \(i\)th Bernstein polynomial hits its maximum when \(t = i/n\), so a Bézier curve is most interested in the \(i\)th control point when \(t = i/n\). So nice!

I learned this all from a great paper by Márton Vaitkus. This stuff is actually well-known, but he goes further. He shows that Bézier curves are related to geometric quantization - in particular the 'Veronese' map from states of the spin-1/2 particle to states of the spin-\(n\)/2 particle, which I wrote about in my September 4th entry.
I love it when ideas form a thick network like this!
Here is Márton Vaitkus' paper:

This galaxy is falling. Dust, which looks brown, is getting stripped off by the hot gas the galaxy is falling through... and the whole galaxy is getting bent. It's falling into the Virgo Cluster, a collection of over 1000 galaxies. The hot intergalactic wind is stripping this galaxy, not only of its dust, but its gas. So it won't be able to form many more stars.
This is called 'ram pressure stripping'. It happens to lots of galaxies. But what's 'ram pressure', exactly?
If Superman ran so fast that the wind ripped off his clothes, that would be 'ram pressure stripping'. You can feel ram pressure from the air when you run through it. This pressure is proportional to the square of your speed. Why?
As a gas moves past, you feel pressure equal to the momentum of the gas molecules hitting you, per area, per time. Their momentum is proportional to their speed. But also the number that hit you per time is proportional to their speed. So: speed squared!
For more on ram pressure, read this Wikipedia article — and be glad I derived it more simply:
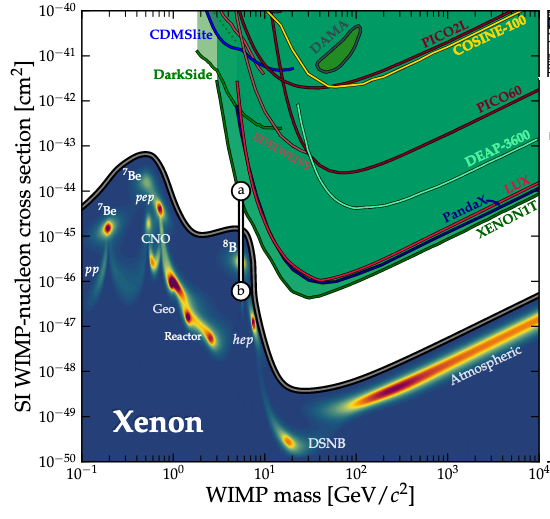
As attempts to detect dark matter particles get better, they'll eventually run into the 'neutrino fog'. Green is where they've already ruled out dark matter particles with various masses and chances of interacting with ordinary matter. Blue is the neutrino fog.
So, the search to detect weakly interacting massive particles by looking for them to collide with atomic nuclei in big tanks of stuff like liquid xenon will not go on forever. It'll end when the fog gets too thick!
This chart is from here:


Sometimes scary-looking math formulas are just common sense when you
think about them the right way. A great example is the
Chu-Vandermonde identity.
September 12, 2021

Some numbers written with just 0's and 1's aren't prime in any base. On Twitter we were discussing this. Tilly asked what fraction of bit strings are not prime in any base, asymptotically, and he easily showed that fraction is at least 1/2: any numeral that ends in 0 can't be prime in any base — except for 10, which is just \(n\) in base \(n\).
I noticed that any bit string consisting of repeated blocks of a fixed string, separated by any number of 0's (including none), cannot be prime in any base. But the asymptotic density of these is zero, I believe, so I rashly conjectured the answer to Ben Tilly's question is 1/2.
In fact Odlyzko and Poonen conjectured in 1993 that asymptotically 1/2 of polynomials with coefficients 0 or 1 are irreducible: that is, you can't factor them in into polynomials of lower degree with integer coefficients. Konyagin has proved a weaker result in this direction:
If this conjecture is true, to settle my conjecture it would be enough to show that any irreducible polynomial \(P\) takes a prime value \(P(n)\) for some natural number \(n \ge 2\). But in fact there's another conjecture, a special case of Schinzel's 'Hypothesis H', saying that if \(P\) is any irreducible polynomial with integer coefficients and a positive leading coefficient then \(P(n)\) is prime for infinitely many positive integers \(n\):

As an undergrad I learned a lot about partial derivatives in physics classes. But they told us rules as needed, without proving them. This rule completely freaked me out. If derivatives are kinda like fractions, shouldn't this equal 1?
Let me show you why it's -1.
First, consider an example:

This example shows that the identity is not crazy. But in fact it holds the key to the general proof! Since \((u,v)\) is a coordinate system we can assume without loss of generality that \(u = x, v = y\). At any point we can approximate \(w\) to first order as \(ax + by + c\) for some constants \(a,b,c\). But for derivatives the constant \(c\) doesn't matter, so we can assume it's zero.
Then just compute!

There's also a proof using differential forms that you might like better. You can see it here, along with an application to thermodynamics:
But this still leaves us yearning for more intuition — and for me at least, a more symmetrical, conceptual proof. Over on Twitter, someone named Postdoc/cake provided some intuition using the same example from thermodynamics:
Using physics intuition to get the minus sign:
- increasing temperature at const volume = more pressure (gas pushes out more)
- increasing temperature at const pressure = increasing volume (ditto)
- increasing pressure at const temperature = decreasing volume (you push in more)
Jules Jacobs gave the symmetrical, conceptual proof that I was dreaming of:
As I'd hoped, the minus signs come from the anticommutativity of the
wedge product of 1-forms, e.g.
$$ du \wedge dv = - dv \wedge du $$
Since the space of 2-forms at a point in the plane is 1-dimensional, we can divide them. In fact a ratio like
$$ \frac{du \wedge dw}{dv \wedge dw}$$
is just the Jacobian of the tranformation from \((v,w)\) coordinates to
\((u,w)\) coordinates. We also need that these ratios obey the rule
$$ \frac{\alpha}{\beta} \cdot \frac{\gamma}{\delta} = \frac{\alpha}{\delta}
\cdot \frac{\gamma}{\beta} $$
where \(\alpha, \beta, \gamma, \delta\) are nonzero 2-forms at a point
in the plane. This seems obvious, but you need to check it. It's not
hard. But to put it in fancy language, it follows from the fact that
nonzero 2-forms at a point in the plane form a torsor for the multiplicative group of nonzero
real numbers!
September 14, 2021

Beginners often bang their heads for a long time on a hard problem, not realizing it's time to switch to a related problem that's a bit easier.
And if that problem is still too hard, switch again. When you finally hit one you can do, work your way back up!
Some quote Pólya as saying "If you can't solve a problem, then there is an easier problem you can solve: find it." It's good to think about why Conway's version, while meant a bit humorously, is better. Pólya's actual remark in his book is longer:

Pólya's book How to Solve It is worth reading —
especially for category theorists and other 'theory-builders', the
sort who don't solve lots of puzzles or do Math Olympiads.
Puzzle-solvers are often better at this stuff.
September 15, 2021
You have to be a bit careful about epimorphisms of rings,
because they aren't always onto. For example the inclusion of the
integers \(\mathbb{Z}\) in the rationals \(\mathbb{Q}\) is an
epimorphism.
What are all the ring epimorphisms \(f \colon \mathbb{Z} \to R\)?
There's always exactly one ring homomorphism from \(\mathbb{Z}\) to any ring \(R\). So, people say a ring is solid if the unique ring homomorphism \(f \colon \mathbb{Z} \to R\) is an epimorphism. My question then becomes: what are all the solid rings?
The most obvious examples are the quotient rings \(\mathbb{Z}/n\). The homomorphism \(f \colon \mathbb{Z} \to \mathbb{Z}/n\) is not just an epimorphism, it's what we call a 'regular' epimorphism: basically a quotient map. The rings \(\mathbb{Z}/n\) are the only rings where the unique morphism from \(\mathbb{Z}\) is a regular epimorphism.
But \(\mathbb{Q}\) is also solid, since once you know what a ring homomorphism \(g\) out of \(\mathbb{Q}\) does to the element \(1\), you know it completely, since \(g(m/n) = g(m)g(n)^{-1}\). For the same reason, any subring of \(\mathbb{Q}\) is solid.
And there are lots of these: in fact, a continuum of them. Take any set of prime numbers. Start with \(\mathbb{Z}\), and throw in the inverses of these primes. You get a subring of \(\mathbb{Q}\). So, there are at least \(2^{\aleph_0}\) subrings of \(\mathbb{Q}\), and clearly there can't be more.
(In fact I've just told you how to get all the subrings of \(\mathbb{Q}\).)
These are the 'obvious' solid rings. But there are lots more! Bousfeld and Kan classified all the commutative solid rings in 1972, in this paper freely available from the evil publisher Elsevier:
For example, let \(\mathbb{Z}[1/2]\) be the ring of dyadic rationals: the subring of \(\mathbb{Q}\) generated by the integers and the number \(1/2\). This is solid. So is \(\mathbb{Z}/2\). We knew that. But the product \(\mathbb{Z}[1/2] \times \mathbb{Z}/2\) is also solid!
More generally, suppose \(R\) is a subring of \(\mathbb{Q}\). \(R \times \mathbb{Z}/n\) is solid if:
Subobjects of the terminal object in a category are called subterminal objects, and they're cool because they look 'no bigger than a point'. The category \(\mathsf{Set}\) has just two, up to isomorphism: the 1-point set, and the empty set.
But a general topos has lots of subterminal objects — and we've seen that the category of affine schemes has lots too. These should be important in algebraic geometry somehow, but I have no idea how.
One year after Bousfeld and Kan's paper, Storrer showed that all solid rings are commutative:
So, we now know the complete classification of solid rings!
September 16, 2021
This picture from 1561 illustrates an old theory of projectile motion. The cannonball shoots out of the cannon, carried along by the wind. Then it drops straight down! Did the guy who drew this believe the theory, or was he making fun of it? I don't know.
This picture from 1592 is less cartoonish. First the cannonball has a phase of "violent motion", then "mixed motion", and finally "natural motion" when it falls straight down. This picture is from a manual of artillery.
If you're laughing at these people for not drawing parabolas, please remember that air friction makes a cannonball drop more steeply than it rises in the first place.
The above picture is from here:
He traces how the invention of guns and cannons forced a rethink of old theories of projectile motion.
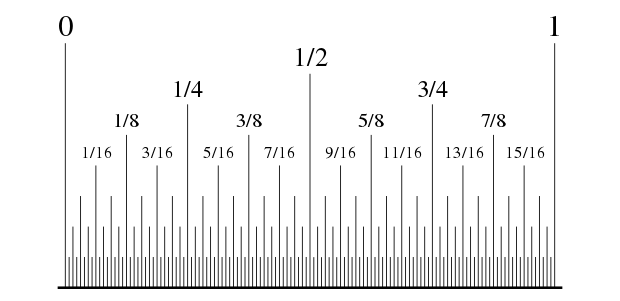
If you've seen an American ruler you've met the dyadic rational numbers: rationals whose denominators are powers of two. You can add, multiply, and subtract these numbers and get numbers of the same kind, so they form a commutative ring.
The ring of dyadic rationals is called \(\mathbb{Z}[1/2]\). But now let's look at the dyadic rationals modulo 1. In other words, take the dyadics from 0 to 1 and bend them around to form a kind of circle by saying 0 is the same as 1. You get this thing:
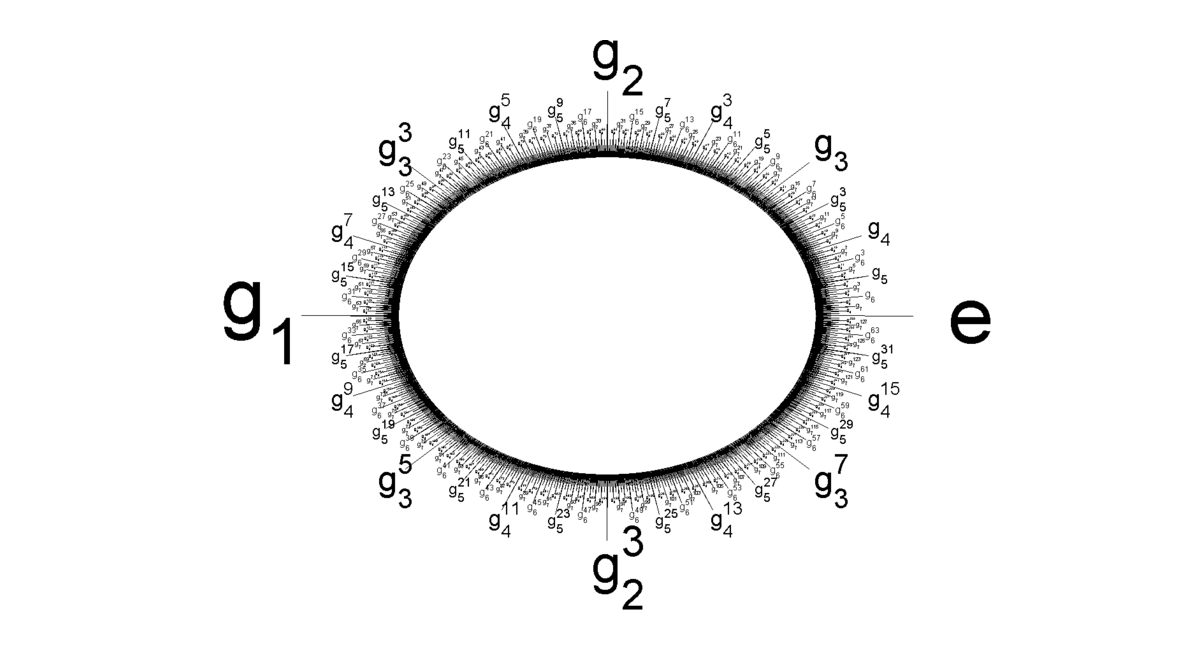
Indeed, the multiplication we had for dyadic rationals doesn't make sense mod 1. But you can still add and subtract dyadic rationals mod 1, for example $$ 7/8 + 2/8 = 1/8 \bmod 1 $$ So this thing is an abelian group — and it's called the Prüfer 2-group. For more on the Prüfer 2-group, check out my blog article:

2-adic integers could be introduced in grade school by teaching kids how to write numbers in base 2 and then talking about numbers that go on forever to the left.
I'm not saying this is a good idea! But the kids could then add them the usual way, with 'carrying'.
To understand this using more math: we can get the group of 2-adic integers as the 'limit' of this diagram of groups, where each is mapped onto the next in the obvious way: $$ \cdots \to \mathbb{Z}/16 \to \mathbb{Z}/8 \to \mathbb{Z}/4 \to \mathbb{Z}/2 $$ Elements of \(\mathbb{Z}/2\) can be written in binary using \(n\) digits. 2-adic integers have infinitely many digits.
The 2-adic integers are the evil twin of the Prüfer 2-group, which I described yesterday. The Prüfer 2-group is the colimit of these groups, each included into the next in the obvious way: $$ \mathbb{Z}/2 \to \mathbb{Z}/4 \to \mathbb{Z}/8 \to \mathbb{Z}/16 \to \cdots $$ The Prüfer 2-group has elements like 0.10111 where the binary expansion does end, and we add mod 1. As I already mentioned, it looks like this:

The technical term for 'evil twin' is 'Pontryagin dual'. The Pontryagin dual of a locally compact abelian group is the set of all continuous homomorphisms from it to the circle. This becomes abelian group under pointwise addition, and we can give it a topology making it a locally compact abelian group again If we treat the Prüfer 2-group as a discrete abelian group, it's locally compact, and its Pontryagin dual is the group of 2-adic integers!
The Pontryagin dual of a discrete abelian group is a compact abelian
group, so the 2-adic integers get a topology that makes them a compact
abelian group. On the other hand, the Pontryagin dual of a compact
abelian group is a discrete abelian group. And taking the Pontryagin
dual twice gets you back where you started! So, the group of
continuous homomorphisms from the 2-adic integers to the circle is the
Prüfer 2-group again!
September 22, 2021
I've been trying to get to the bottom of 'Maxwell's relations' in
thermodynamics. Physically speaking, they boil down to this — namely,
conservation of energy.

Mathematically, this implies \(TdS - PdV\) is an 'exact 1-form', meaning $$ TdS - PdV = dU $$ for some function \(U\). We call \(U\) the 'internal energy' of the system. Since \(d^2 U = 0\), this gives $$ dT \wedge dS - dP \wedge dV = 0 $$ or $$ dT \wedge dS = dP \wedge dV $$ From here we can quickly get all four of Maxwell's relations! In this post I explain how:

Until digital media took over, TV studios were constantly erasing their tapes in order to save money — so if Marion Stokes hadn't recorded her own TVs for 33 years, making 71,716 video tapes and storing them in apartments she rented, there would be a big hole in modern history!
She videotaped the TV news on up to 8 VCRs from 1977 until 2012, when she died at the age of 83. Every six hours when the tapes were about to end, Stokes and her husband ran around to switch them out — even cutting short meals at restaurants! In her later years she got someone to help her.
She was a civil rights demonstrator, activist and librarian. She was convinced that there was a lot of detail in the news at risk of disappearing forever.
Her work is now being uploaded to the Internet Archive. Read more here:

Why isn't time an observable in quantum mechanics? And how do you prove the time-energy uncertainty relation that I just stated? I explain it all here: