For my November 2024 diary, go here.

Diary — December 2024

John Baez

Lisa asked Oxford University Press for a copy of Aristotle's Fragmenta Selecta in return for reviewing a book. It arrived all busted up.

Is this someone's idea of a joke? A fragmented Fragmenta?

December 2, 2024

Near the end of December 2020, I saw Jupiter and Saturn very close in the sky just after sunset. I didn't know this was called a great conjunction. The next one will happen in November 2040. And it will happen in a very different part of the sky: close to 120° away.

This is how it always works. People have known this for millennia. They just forgot to teach me about it in school. The time between great conjunctions is always roughly 20 years, and if you keep track of them, each one is roughly 120 to the east of the last. Thus, they trace out enormous equilateral triangles in the sky.

Almost equilateral. These triangles drift slightly over time! This picture, drawn by Johannes Kepler in 1606, shows how it works:

After three great conjunctions, 60 years later, we get back to a great conjunction in almost the same place in the sky, but it's shifted east by roughly 7¼ degrees.

Kepler was not just an astronomer: he earned money working as an astrologer. Astrologers divide the sky into 12 zones called houses of the zodiac. These 12 houses are divided into 4 groups of 3 called triplicities. Successive great conjunctions usually loop around between 3 corners of a triplicity — but due to the gradual drifting they eventually move on to the next triplicity.

Astrologers connected these triplicities to the 4 classical elements:

• Fire – Aries, Leo, Sagittarius – hot, dry
• Earth – Taurus, Virgo, Capricorn – cold, dry
• Air – Gemini, Libra, Aquarius – hot, wet
• Water – Cancer, Scorpio, Pisces – cold, wet

Yeah, now things are getting weird. They were taking solid facts and running too far with them, kinda like string theorists.

Anyway: the great conjunctions stay within one triplicity for about 260 years... but then they drift to the next triplicity. This event is called a greater conjunction, and naturally astrologers thought it's a big deal.

(They still do.)

Here's a nice picture of the triplicities. The 12 houses of the zodiac are arbitrary human conventions, as is their connection to the 4 classical elements (earth, fire, water and air). But the triangles have some basis in reality, since the great conjunctions of Saturn and Jupiter approximately trace out equilateral triangles.

The actual triangles formed by great conjunctions drift away from this idealized pattern, as I noted. But if you're a mathematician, you can probably feel the charm of this setup, and see why people liked it!

People look for patterns, and we tend to hope that simple patterns are 'the truth'. If we make a single assumption not adequately grounded by observation, like that the motions of the planets affect human affairs, or that every elementary particle has a superpartner we haven't seen yet, we can build a beautiful framework based which may have little to do with reality.

Since ancient times, ancient astrologers actually knew about the gradual drift of the triangles formed by great conjunctions. And they realized these triangles would eventually come back to same place in the sky! In fact, based on section 39d of Plato's Timaeus, some thought that after some long period of time all the planets would come back to the exact same positions. This was called the Great Year.

A late 4th-century Neoplatonist named Nemesius got quite excited by this idea. In his De natura hominis, he wrote:

The Stoics say that the planets, returning to the same point of longitude and latitude which each occupied when first the universe arose, at fixed periods of time bring about a conflagration and destruction of things; and they say the universe reverts anew to the same condition, and that as the stars again move in the same way everything that took place in the former period is exactly reproduced. Socrates, they say, and Plato, will again exist, and every single man, with the same friends and countrymen; the same things will happen to them, they will meet with the same fortune, and deal with the same things.

My hero the mathematician Nicole Oresme argued against this 'eternal recurrence of the same' by pointing out it could only happen if all the planet's orbital periods were rational multiples of each other, which is very unlikely. I would like to learn the details of his argument. He almost seems to have intuited that rational numbers are a set of measure zero!

But as the historian J. D. North wrote, the subtle mathematical arguments of Oresme had about as much effect on astrologers as Zeno's arguments had on archers. Only slightly more impactful was Étienne Tempier, the Bishop of Paris, who in his famous Condemnation of 1277 rejected 219 propositions, the sixth being

That when all the celestial bodies return to the same point, which happens every 36,000 years, the same effects will recur as now.

For him, an eternal recurrence of endless Jesus Christs would have been repugnant.

The figure of 36,000 years was just one of many proposed as the length of the Great Year. Some astrologers thought the triangle formed by three successive great conjunctions rotates a full turn every 2400 years. If so, this would happen 15 times every Great Year.

But we'll see that figure of 2400 years is a bit off. I get something closer to 2650 years.

The math

• how long it takes for Jupiter to orbit the Sun (about 12 years),

• how long it takes for Saturn to orbit the Sun (about 29 years).

But we need to know these numbers much more precisely! In fact the orbital period of Jupiter is 4332.59 days, while that of Saturn is 10759.22 days. So, Jupiter is moving around the Sun at a rate of

while Saturn is moving more slowly, at

Thus, relative to Saturn, Jupiter is moving around at

Thus, Jupiter makes a full orbit relative to Saturn, coming back to the same location relative to Saturn, every

This idea works for any pair of planets, and it's called the synodic period formula. So now we just calculate! It takes

for Jupiter to make a complete orbit relative to Saturn, coming back to the same place relative to Saturn. So this is the time between great conjunctions: somewhat less than 20 years.

How many orbits around the Sun does Jupiter make during this time? About

This is close to 1⅔. Nobody knows why. It means there's a near-resonance between the orbits of Jupiter and Saturn — but their orbits don't seem to be locked into this resonance by some physical effect, so most astronomers think it's a coincidence.

Since ⅔ of 360° is 240°, and the planets are moving east, meaning counterclockwise when viewed looking down from far above the Earth's north pole, each great conjunction is displaced roughly 240° counterclockwise from the previous one — or in other words, 120° clockwise. If you're confused, look at Kepler's picture!

But 1.67416 is not exactly 1⅔. The difference is

of an orbit. In terms of degrees, this is

After three great conjunctions we get another one in almost the same place, but it's shifted by

Hmm, this doesn't match the figure of 7¼ that I quoted earlier. I got that, and a lot of this fascinating material, from a wonderful essay called 'Astrology and the fortunes of churches' in this book:

• J. D. North, Stars, Minds and Fate: Essays in Ancient and Medieval Cosmology, The Hambledon Press, London, 1989.

I don't know why the figures don't match.

Anyway, I am trying to figure out how many great conjunctions are required for the near-equilateral triangle in Kepler's picture to turn all the way around. If it really makes 0.00750 of a full turn every 7253.46 days, as I've calculated, then it makes a full turn after

This actually matches pretty well the estimate of 2600 years given by the great Persian astrologer Abū Ma‘shar al-Balkhi, who worked in the Abbasid court in Baghdad starting around 830 AD. It was his works, under the Latinized name of Albumasar, that brought detailed knowledge of the great conjunction to Europe.

So, I think I did okay. I have ignored various subtleties. Most importantly, the timing of great conjunctions as seen from Earth, rather than from the Sun, are complicated by the motion of the Earth around the Sun, which significantly affects what we see. Instead of happening at equally spaced intervals of 19 years, 313 days and 17 hours, the duration between great conjunctions as seen here ranges from roughly 18 years 10 months to 20 years 8 months.

You can see a listing of all great conjunctions from 1200 AD to 2400 AD here. Kepler witnessed one in December of 1603. He theorized that the Star of Bethlehem was a great conjunction, and computed that one occurred in 7 BC.

For more, see:

• D. V. Etz, Conjunctions of Jupiter and Saturn, Journal of the Royal Astronomical Society of Canada 94 (2000), 174–178.

Here is a movie of the December 21, 2020 great conjunction taken by ProtoSlav:

Click on this picture and others to see where I got them.

December 7, 2024

This is sometimes painted as a sudden triumph of rationality over the foolish yet long-standing belief that the Sun and all the planets revolve around the Earth. As usual, this triumphalist narrative is oversimplified. In the history of science, everything is always more complicated than you think.

First, Aristarchus had come up with a heliocentric theory way back around 250 BC. While Copernicus probably didn't know all the details, he did know that Aristarchus said the Earth moves. Copernicus mentioned this in an early unpublished version of De revolutionibus.

Copernicus also had some precursors in the Middle Ages, though it's not clear whether he was influenced by them.

In the 1300's, the philosopher Jean Buridan argued that the Earth might not be at the center of the Universe, and that it might be rotating. He claimed — correctly in the first case, and only a bit incorrectly in the second — that there's no real way to tell. But he pointed out that it makes more sense to have the Earth rotating than have the Sun, Moon, planets and stars all revolving around it, because

it is easier to move a small thing than a large one.

Yet everyone holds, and I think myself, that the heavens do move and not the Earth, for "God created the orb of the Earth, which will not be moved" [Psalms 104:5], notwithstanding the arguments to the contrary.

Martianus Capella

Sometime between 410 and 420 AD, Martianus Capella came out with a book saying Mercury and Venus orbit the Sun, while the other planets orbit the Earth!

This picture is from a much later book by the German astronomer Valentin Naboth, in 1573. But it illustrates Capella's theory — and as we'll see, his theory was rather well-known in western Europe starting in the 800s.

First of all, take a minute to think about how reasonable this theory is. Mercury and Venus are the two planets closer to the Sun than we are. So, unlike the other planets, we can never possibly see them more than 90° away from the Sun. In fact Venus never gets more than 48° from the Sun, and Mercury stays even closer. So it looks like these planets are orbiting the Sun, not the Earth!

But who was this guy, and why did he matter?

Martianus Capella was a jurist and writer who lived in the city of Madauros, which is now in Algeria, but in his day was in Numidia, one of six African provinces of the Roman Empire. He's famous for a book with the wacky title De nuptiis Philologiae et Mercurii, which means On the Marriage of Philology and Mercury. It was an allegorical story, in prose and verse, describing the courtship and wedding of Mercury (who stood for "intelligent or profitable pursuit") and the maiden Philologia (who stood for "the love of letters and study"). Among the wedding gifts are seven maids who will be Philology's servants. They are the seven liberal arts:

• The Trivium: Grammar, Dialectic, Rhetoric.
• The Quadrivium: Geometry, Arithmetic, Astronomy, Harmony.

In seven chapters, the seven maids explain these subjects. What matters for us is the chapter on astronomy, which explains the structure of the Solar System.

This book De nuptiis Philologiae et Mercurii became very important after the decline and fall of the Roman Empire, mainly as a guide to the liberal arts. In fact, if you went to a college that claimed to offer a liberal arts education, you were indirectly affected by this book!

Here is a painting by Botticelli from about 1485, called A Young Man Being Introduced to the Seven Liberal Arts:

The Carolingian Renaissance

I'm no expert on this, but it seems as the Roman Empire declined there was a gradual dumbing down of scholarship, with original and profound works by folks like Aristotle, Euclid, and Ptolemy eventually being lost in western Europe — though preserved in more civilized parts of the world, like Baghdad and the Byzantine Empire. In the west, eventually all that was left were easy-to-read popularizations by people like Pliny the Elder, Boethius, Macrobius, Cassiodorus... and Martianus Capella!

By the end of the 800s, many copies of Capella's book De nuptiis Philologiae et Mercurii were available. Let's see how that happened!

Expansion of the Franks

To set the stage: Charlemagne became King of the Franks in 768 AD. Being a forward-looking fellow, he brought in Alcuin, headmaster of the cathedral school in York and "the most learned man anywhere to be found", to help organize education in his kingdom.

Alcuin set up schools for boys and girls, systematized the curriculum, raised the standards of scholarship, and encouraged the study of liberal arts. Yes: the liberal arts as described by Martianus Capella! For Alcuin this was all in the service of Christianity. But scholars, being scholars, took advantage of this opportunity to start copying the ancient books that were available, writing commentaries on them, and the like.

In 800, Charlemagne became emperor of what's now called the Carolingian Empire. When Charlemagne died in 814 a war broke out, but it ended in 847. Though divided into three parts, the empire flourished until about 877, when it began sinking due to internal struggles, attacks from Vikings in the north, etc.

The heyday of culture in the Carolingian Empire, roughly 768–877, is sometimes called the Carolingian Renaissance because of the flourishing of culture and learning brought about by Alcuin and his successors. To get a sense of this: between 550 and 750 AD, only 265 books have been preserved from Western Europe. From the Carolingian Renaissance we have over 7000.

However, there was still a huge deficit of the classical texts we now consider most important. As far as I can tell, the works of Aristotle, Eratosthenes, Euclid, Ptolemy and Archimedes were completely missing in the Carolingian Empire. I seem to recall that from Plato only the Timaeus was available at this time. But Martianus Capella's De nuptiis Philologiae et Mercurii was very popular. Hundreds of copies were made, and many survive even to this day! Thus, his theory of the Solar System, where Mercury and Venus orbited the Sun but other planets orbited the Earth, must have had an out-sized impact on cosmology at this time.

Here is part of a page from one of the first known copies of De nuptiis Philologiae et Mercurii:

It's called VLF 48, and it's now at the university library in Leiden. Most scholars say it dates to 850 AD, though Mariken Teeuwen has a paper claiming it goes back to 830 AD.

You'll notice that in addition to the main text, there's a lot of commentary in smaller letters! This may have been added later. Nobody knows who wrote it, or even whether it was a single person. It's called the Anonymous Commentary. This commentary was copied into many of the later versions of the book, so it's important.

The Anonymous Commentary

Alas, now I need to throw a wet blanket on that, and show how poorly Martianus Capella's cosmology was understood at this time!

The Anonymous Commentary actually describes three variants of Capella's theory of the orbits of Mercury and Venus. One of them is good, one seems bad, and one seems very bad. Yet subsequent commentators in the Carolingian Empire didn't seem to recognize this fact and discard the bad ones.

These three variants were drawn as diagrams in the margin of VLF 48, but Robert Eastwood has nicely put them side by side here:

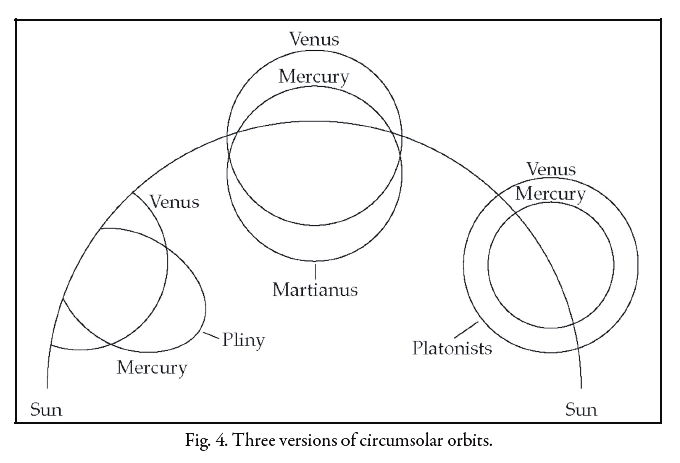
The one at right, which the commentary attributes to the "Platonists", shows the orbit of Mercury around the Sun surrounded by the larger orbit of Venus. This is good.

The one in the middle, which the commentary attributes to Martianus Capella himself, shows the orbits of Mercury and Venus crossing each other. This seems bad.

The one at left, which the commentary attributes to Pliny, shows orbits for Mercury and Venus that are cut off when they meet the orbit of the Sun, not complete circles. This seems very bad — so bad that I can't help but hope there's some reasonable interpretation that I'm missing. (Maybe just that these planets get hidden when they go behind the Sun?)

Robert Eastwood attributes the two bad models to a purely textual approach to astronomy, where commentators tried to interpret texts and compare them to other texts, without doing observations. I'm still puzzled.

Copernicus

That's 30 years after Copernicus came out with his book... but the clarification probably happened earlier. And Copernicus did mention Martianus Capella's work. In fact, he used it to argue for a heliocentric theory! In Chapter 10 of De Revolutionibus he wrote:

In my judgement, therefore, we should not in the least disregard what was familiar to Martianus Capella, the author of an encyclopedia, and to certain other Latin writers. For according to them, Venus and Mercury revolve around the sun as their center. This is the reason, in their opinion, why these planets diverge no farther from the sun than is permitted by the curvature of their revolutions. For they do not encircle the earth, like the other planets, but "have opposite circles". Then what else do these authors mean but that the center of their spheres is near the sun? Thus Mercury's sphere will surely be enclosed within Venus', which by common consent is more than twice as big, and inside that wide region it will occupy a space adequate for itself. If anyone seizes this opportunity to link Saturn, Jupiter, and Mars also to that center, provided he understands their spheres to be so large that together with Venus and Mercury the earth too is enclosed inside and encircled, he will not be mistaken, as is shown by the regular pattern of their motions.

For [these outer planets] are always closest to the earth, as is well known, about the time of their evening rising, that is, when they are in opposition to the sun, with the earth between them and the sun. On the other hand, they are at their farthest from the earth at the time of their evening setting, when they become invisible in the vicinity of the sun, namely, when we have the sun between them and the earth. These facts are enough to show that their center belongs more to then sun, and is identical with the center around which Venus and Mercury likewise execute their revolutions.

Conclusion

• In classic geocentrism, the Earth was non-rotating and everything revolved around it.
• Buridan and Oresme strongly considered the possibility that the Earth rotated... but not, apparently, that it revolved around the Sun.
• Capella believed Mercury and Venus revolved around the Sun... but the Sun revolved around the Earth.
• Copernicus believed the Earth rotates, and also revolves around the Sun.
• And to add to the menu, Tycho Brahe, coming after Copernicus, argued that all the planets except Earth revolve around the Sun, but the Sun and Moon revolve around the Earth, which is fixed.

This diversity of theories is fascinating... even though everyone holds, and I think myself, that the Earth revolves around the Sun.

Above is a picture of the "Hypothesis Tychonica", from a book written in 1643.

References

You King Gelon are aware the 'universe' is the name given by most astronomers to the sphere the centre of which is the centre of the earth, while its radius is equal to the straight line between the centre of the sun and the centre of the earth. This is the common account as you have heard from astronomers. But Aristarchus has brought out a book consisting of certain hypotheses, wherein it appears, as a consequence of the assumptions made, that the universe is many times greater than the 'universe' just mentioned. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun on the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of fixed stars, situated about the same centre as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the centre of the sphere bears to its surface.

For Aristarchus' influence on Copernicus, see:

• Owen Gingerich, Did Copernicus owe a debt to Aristarchus?, Journal for the History of Astronomy 16 (1985), 37–42.

And if we should admit that the motion of the Sun and Moon could be demonstrated even if the Earth is fixed, then with respect to the other wandering bodies there is less agreement. It is credible that for these and similar causes (and not because of the reasons that Aristotle mentions and rejects), Philolaus believed in the mobility of the Earth and some even say that Aristarchus of Samos was of that opinion. But since such things could not be comprehended except by a keen intellect and continuing diligence, Plato does not conceal the fact that there were very few philosophers in that time who mastered the study of celestial motions.

• John Buridan, Questions on the Four Books on the Heavens and the World of Aristotle, Book II, Question 22, trans. Michael Claggett, in The Science of Mechanics in the Middle Ages, University of Wisconsin Press, Madison, Wisconsin, 1961, pp. 594–599.

• Nicole Oresme, On the Book on the Heavens and the World of Aristotle, Book II, Chapter 25, trans. Michael Claggett, in The Science of Mechanics in the Middle Ages, University of Wisconsin Press, Madison, Wisconsin, 1961, pp. 600–609.

William Harris Stahl, Evan Laurie Burge and Richard Johnson, eds., Martianus Capella and the Seven Liberal Arts: The Marriage of Philology and Mercury. Vol. 2., Columbia University Press, 1971.

• Dusan Nikolic, What was the Carolingian Renaissance?, 2023 April 6.

• Bruce S. Eastwood, Ordering the Heavens: Roman Astronomy and Cosmology in the Carolingian Renaissance, Brill, 2007.

• Mariken Teeuwen and Sínead O'Sullivan, eds., Carolingian Scholarship and Martianus Capella: Ninth-Century Commentary Traditions on De nuptiis in Context, The Medieval Review (2012).

• Bruce S. Eastwood, The power of diagrams: the place of the anonymous commentary in the development of Carolingian astronomy and cosmology.

• Mariken Teeuwen, Writing between the lines: reflections of a scholarly debate in a Carolingian commentary tradition.

For the full text of Copernicus' book, translated into English, go here.

December 20, 2024

By this time each planet had been provided with from 40 to 60 epicycles to represent after a fashion its complex movement among the stars.

Medieval astronomers did not use so many epicycles. The Alfonsine Tables, which the Brittanica is mocking above, actually computed planetary orbits using the method in Ptolemy's Almagest, developed way back in 150 AD. This method uses at most 31 circles and spheres — nothing like Britannica's ridiculous claim of between 40 to 60 epicycles per planet.

The key idea in Ptolemy's model was this:

The blue dot here is the Earth. The large black circle, offset from the Earth, is called a 'deferent'. The smaller black circle is called an 'epicycle'. The epicycle makes up for how in reality the Earth is not actually stationary, but moving around the Sun.

The center of the epicycle rotates at constant angular velocity around the purple dot, which is called the 'equant'. The equant and the Earth are at equal distances from the center of the black circle. Meanwhile the planet, in red, moves around the center of the epicycle at constant angular velocity.

In the Almagest, Ptolemy used some additional cycles to account for how the latitudes of planets change over time. In reality this happens because the planets don't all move in the same plane. Ptolemy also used additional 'epicyclets' to account for peculiarities in the orbits of Mercury and the Moon, and a mechanism to account for the precession of equinoxes — which really happens because the Earth's axis is slowly precessing.

In a later work, the Planetary Hypothesis, achieved even more accurate results with fewer cycles, by having the planets orbit in different planes (as they indeed do).

So, just because something is in an encyclopedia, or even an encyclopædia, doesn't mean it's true.

The Encyclopædia Britannica quote comes from their 1968 edition, volume 2, in the article on the Spanish king Alfonso X, which on page 645 discusses the Alfonsine Table commissioned by this king:

By this time each planet had been provided with from 40 to 60 epicycles to represent after a fashion its complex movement among the stars. Amazed at the difficulty of the project, Alfonso is credited with the remark that had he been present at the Creation he might have given excellent advice.

In The Book Nobody Read, Owen Gingerich writes that he challenged Encyclopædia Britannica about the number of epicycles. Their response was that the original author of the entry had died and its source couldn't be verified. Gingerich has also expressed doubts about the quotation attributed to King Alfonso X.

For the controversy over whether medieval astronomers used lots of epicycles, start here:

• Wikipedia, Deferent and epicycle: history.

• Wikipedia, Deferent and epicycle: the number of epicycles.

Then dig into the sources! For example, Wikipedia says the claim that the Ptolemaic system uses about 80 circles seems to have appeared in 1898. It may have been inspired by the non-Ptolemaic system of Girolamo Fracastoro, who used either 77 or 79 orbs. So some theories used lots of epicycles — but not the most important theories, and nothing like the 240-360 claimed by the 1968 Brittanica.

Owen Gingerich wrote The Book Nobody Read about his quest to look at all 600 extant copies of Copernicus' De revolutionibus. The following delightful passage was contributed by pglpm on Mastodon:

A farmer with a wolf, a goat, and a cabbage must cross a river by boat. The boat can carry only the farmer and a single item. If left unattended together, the wolf would eat the goat, or the goat would eat the cabbage. How can they cross the river without anything being eaten?

You probably know this puzzle. There are two efficient solutions, related by a symmetry that switches the wolf and the cabbage.

But what you might not know is that this puzzle goes back to a book written around 800 AD, sometimes attributed to Charlemagne's advisor Alcuin! Charlemagne brought this monk from York to help set up the educational system of his empire. But Alcuin had a great fondness for logic. Nobody is sure if he wrote this book — but it's fascinating nonetheless.

It has either 53 or 56 logic puzzles, depending on the version. It's called Propositiones ad Acuendos Juvenes, or Problems to Sharpen the Young. If the wolf, goat and cabbage problem is too easy for you, you might like this one:

Three men, each with a sister, must cross a boat which can carry only two people, so that a woman whose brother is not present is never left in the company of another man.

A man has 300 pigs. He ordered all of them slaughtered in 3 days, but with an odd number killed each day. What number were to be killed each day?

It's fascinating to think that while some Franks were fighting Saxons and Lombards, students in more peaceful parts of the empire were solving these puzzles!

The book also has some of the first recorded packing problems, like this:

There is a triangular city which has one side of 100 feet, another side of 100 feet, and a third of 90 feet. Inside of this, I want to build rectangular houses in such a way that each house is 20 feet in length, 10 feet in width. How many houses can I fit in the city?

• Nikolai Yu. Zolotykh, Alcuin's Propositiones de Civitatibus: the earliest packing problems.

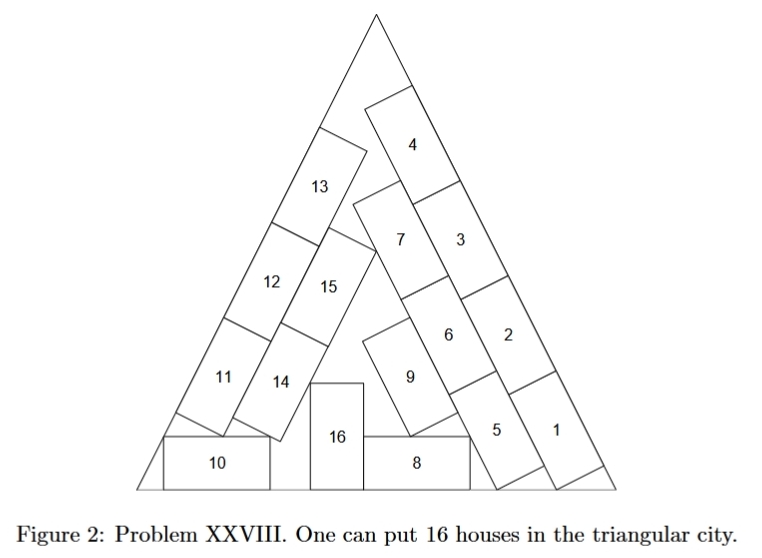
However, Alcuin — or whoever wrote the book — didn't really solve the problem. They just used an approximate Egyptian formula for the area of a triangle in terms of its side lengths, and divided that by the area of the houses! This is consistent with the generally crappy knowledge of math in Charlemagne's empire.

There's an even harder packing problem in this book, which again isn't solved correctly.

For more on this book of puzzles, check out this:

• Wikipedia, Propositiones ad Acuendos Juvenes.

• John Hadley and David Singmaster, Problems to Sharpen the Young, The Mathematical Gazette 76 (1992), 102–126.

• Michael N. Brennan, Alcuin, mathematics and the rational mind, in Insular Iconographies: Essays in Honor of Jane Hawkes, eds. Meg Boulton and Michael D. J. Bintley, Boydell Press, 2019, pp. 203–216.

A medieval mathematical manuscript

The medieval cleric Alcuin (AD 735–804) is credited in surviving manuscripts with being the originator of a collection of fifty-three mathematical and logical puzzles, the Propositiones ad acuendos iuvenes (‘Problems for Sharpening the Young’). There is no direct evidence to connect the collection with Alcuin either as compiler or creator, but even modern commentators continue to associate his name with the puzzles. There are at least fourteen extant or partial copies of the Propositiones, which date from the ninth to the fifteenth century, suggesting that the collection was in popular use at least from the time of Alcuin onwards. Michael Gorman confidently listed the Propositiones among ninety spurious prose works of Alcuin for two reasons: firstly, because Alcuin always attached a dedicatory letter to his works, and there is none here, and secondly, because the work falls, Gorman thinks, among those documents which Alcuin would have had neither the time nor the energy to write in the period AD 782–800. Alcuin himself admitted to having only ‘stolen hours’ at night in which to write a life of Willibrord. Despite Gorman’s view that the work is pseudo-Alcuin, it is reasonable to ask if there is internal evidence in the puzzles which would support or oppose the assigning of the collection to Alcuin himself, committed as he was to the promotion of educational subjects, including mathematics, in the course of the Carolingian ‘renaissance’.

The majority of the problem types in the Propositiones are known from earlier Chinese, Indian, Egyptian, Byzantine, Greek, and Roman sources, whilst others appear in works by Boethius, Metrodorus, and Isidore of Seville. Among the puzzles, however, there are a small number of important types that are not as yet known from earlier sources. These include the so-called ‘river-crossing problems’, ‘strange family problems’, a transportation (or ‘desert-crossing’) problem, and a problem that relies on the summation of an arithmetical series. The case for the mathematical creativity of the author, if there was only one author, rests on these. One puzzle has outstripped all the others in having popular appeal down to the present day. This puzzle, passing presumably from later medieval reproductions of the Propositiones into oral tradition, concerns a farmer who needs to ferry three items across a river in a boat.

Did Alcuin compose the Propositiones?

In a letter to Charlemagne in AD 799, three years after Alcuin had moved from the Palace School to an abbacy at Tours, Alcuin wrote that he was sending, along with some examples of grammar and correct expression, quidquid figuras arithmeticas laetitiae causa (‘certain arithmetical curiosities for [your] pleasure’). He added that he would write these on an empty sheet that Charlemagne sent to him and suggested that ‘our friend and helper Beselel will [...] be able to look up the problems in an arithmetic book’. Beselel was Alcuin’s nickname for the technically skilled Einhard, later Charlemagne’s biographer. It would be convenient if the reference in Alcuin’s letter were to the Propositiones, but for many reasons it is almost certainly not. For one thing, fifty-three propositions and their solutions would not fit on the blank side of a folio, given that they occupy ten folio sides in most of the manuscripts in which they are currently found. Secondly, since Alcuin’s letter to Charlemagne dealt primarily with the importance of exactness of language, a grammarian and self-conscious Latinist like Alcuin would not describe the Propositiones as figurae arithmeticae, or refer to an ‘arithmetic’ book in a case where the solutions required both geometry and logic methods. Thirdly, the idea of Einhard looking up the problems in an arithmetic book is an odd one, given that the Propositiones is usually found with answers, even if in most cases it does not show how these answers were arrived at.

Apart from the reasons given by Gorman for Alcuin not having been the author of the Propositiones — the effort and time involved and the absence of a dedication — there are deeper, internal reasons for concluding that Alcuin was not the author. The river-crossing puzzles, along with the ‘transportation problem’, and a puzzle about the number of birds on a100-step ladder took a considerable amount of time and mathematical sophistication to compose. Accompanying them are two types of puzzles that appear repeatedly in the collection and that demand far lesssophistication: area problems, often fanciful (such as problem 29: ‘how many rectangular houses will fit into a town which has a circular wall?’); and division problems where a ‘lord of the manor’ wishes to divide grain among his household (problems 32–5, and others). Repetition of problems suggests that the Propositiones was intended for use as a practice book, but this supposed pedagogical purpose stumbles (even if it does not fall) on two counts. Firstly, the solutions to most of the mensuration problems, like the one involving a circular town, rely on late Roman methods for approximating the areas of common figures (circles, triangles, etc.) and these methods can be quite wrong. Secondly, the lack of worked solutions in the Propositiones deprived the student of the opportunity to learn the method required to solve another question of the same type. Solution methods might have been lost in transcription, but their almost total absence makes this unlikely. Mathematical methods (algebra in particular) that post-dated the Carolingian era would have been necessary to provide elegant and instructive solutions to many of the problems, and one cannot escape the suspicion that trial-and-error was the method used by whoever supplied answers (without worked solutions) to the Propositiones: a guess was made, refined, and then a new guess made. Such an approach is difficult to systemise, and even more difficult to describe in writing for the benefit of students. We are left with a mixture of ‘complex’ mathematical problems, such as those cited earlier, and simpler questions whose answers are mostly not justified.

This lack of uniformity suggests that it was a compiler rather than a composer who produced the first edition of the Propositiones. If Alcuin was involved, he was no more than a medium through which the fifty-three puzzles were assembled. No one person was the author of the Propositiones problems, because no mathematically sophisticated person would have authored the weaker ones, and nobody who was not mathematically sophisticated could have authored the others. Furthermore, with the more sophisticated problems, there is a noticeable absence of the kind of refinement and repetition that is common in modern textbooks.

Today, December 24th 2024, the Parker Solar Probe got 7 times closer to the Sun than any spacecraft ever has, going faster than any spacecraft ever has — 690,000 kilometers per hour. WHEEEEEE!!!!!!!

But the newspapers are barely talking about the really cool part: what it's like down there. The Sun doesn't have a surface like the Earth does, since it's all just hot ionized gas, called 'plasma'. But the Sun has an 'Alfvén surface' — and the probe has penetrated that.

What's the Alfvén surface? In simple terms, it's where the solar wind — the hot ionized gas emitted by the Sun — breaks free of the Sun and shoots out into space. But to understand how cool this is, we need to dig a bit deeper.

After all, how can we say where the solar wind "breaks free of the Sun"?

Hot gas shoots up from the Sun, faster and faster due to its pressure, even though it's pulled down by gravity. At some point it goes faster than the speed of sound! This is the Alfvén surface. Above this surface, the solar wind becomes supersonic, so no disturbances in its flow can affect the Sun below.

It's sort of like the reverse of a black hole! Light emitted from within the event horizon of a black hole can't get out. Sound emitted from outside the Alfvén surface of the Sun can't get in.

Or, it's like the edge of a waterfall, where the water starts flowing so fast that waves can't make it back upstream.

That's pretty cool. But it's even cooler than this, because 'sound' in the solar wind is very different from sound on Earth. Here we have air. The Sun has ions — atoms of gas so hot that electrons have been ripped off — interacting with powerful magnetic fields. You can visualize these fields as tight rubber bands, with the ions stuck to them. They vibrate back and forth together!

You could call these vibrations 'sound', but the technical term is Alfvén waves. Alfvén was the one who figured out how fast these waves move. Parker studied the surface where the solar wind's speed exceeds the speed of the Alfvén waves.

And now we've gone deep below that surface!

This realm is a strange one, and the more we study it, the more complex it seems to get.

You've probably heard the joke that ends "consider a spherical cow". Parker's original model of the solar wind was spherically symmetric, so he imagined the solar wind shooting straight out of the Sun in all directions. In this model, the Alfvén surface is the sphere where the wind becomes faster the Alfvén waves. There are some nice simple formulas for all this.

But in fact the Sun's surface is roiling and dynamic, with sunspots making solar flares, and all sorts of bizarre structures made of plasma and magnetic fields, like spicules, 'coronal streamers' and 'pseudostreamers'... aargh, too complicated for me to understand. This is an entire branch of science!

So, the Alfvén surface is not a mere sphere: it's frothy and randomly changing. The Parker Solar Probe will help us learn how it works — along with many other things.

Finally, here's something mindblowing. There's a red dwarf star 41 light years away from us, called TRAPPIST-1, which may have six planets beneath its Alfvén surface! This means these planets can create Alfvén waves in the star's atmosphere. Truly the music of the spheres!

For more, check out these articles:

• Wikipedia, Alfvén wave.
• Wikipedia, Alfvén surface.

• Steven R. Cranmer, Rohit Chhiber, Chris R. Gilly, Iver H. Cairns, Robin C. Colaninno, David J. McComas, Nour E. Raouafi, Arcadi V. Usmanov, Sarah E. Gibson and Craig E. DeForest, The Sun’s Alfvén surface: recent insights and prospects for the Polarimeter to Unify the Corona and Heliosphere (PUNCH), Solar Physics 298 (2023).

Combined with recent perihelia of Parker Solar Probe, these studies seem to indicate that the Alfvén surface spends most of its time at heliocentric distances between about 10 and 20 solar radii. It is becoming apparent that this region of the heliosphere is sufficiently turbulent that there often exist multiple (stochastic and time-dependent) crossings of the Alfvén surface along any radial ray.

For my January 2025 diary, go here.

home