
In a strange change of focus, I've been getting into Stravinsky very heavily for the last month — listening to almost no other music, and reading a book about his music, and really enjoying it:
I'd known and loved Agon earlier, and also another piece, the Dumbarton Oaks Concerto. This is a much sweeter piece, from Stravinsky's neoclassical period, but it still has the dry, crisp sound he often favored in his later years: a small orchestra, light on strings and heavy on wind instruments.
But I had never heard Variations: Aldous Huxley in memoriam, Stravinsky's last big orchestral composition, written starting in 1963 in memory of his friend Aldous Huxley. I love the ascending strings near the start: they sound like they're falling up, and we know we're in a new world.
Since serialism started with Schoenberg, it was natural for me to drift into Schoenberg too. Stravinsky and Schoenberg both lived in LA! They were competitors, and only talked to each other once, and Stravinsky only took up Schoenberg's ideas after Schoenberg died.
Now I'm getting into Schoenberg. I'd been a bit brainwashed into thinking Schoenberg's music was unpleasant: people act like it's very dissonant, maybe screeching and crunching. I don't like his vocal music much yet — too much high-pitched soprano for my taste — but I'm really getting into his piano music (which I'd always liked, as much as I knew of it) and now his string quartets (which I've owned for ages, but been scared to listen to). You can currently hear all four of his string quartets played by the Arditti quartet on YouTube. I'm enjoying his fourth:
Schoenberg's string quartets are definitely intense, but no more than, say, rock music or heavy metal. In fact they're much smoother in timbre, just harmonically and rhythmically complex, with constantly changing moods. They're not at all restful, but they're easy enough for me to follow, not at all 'random' — and tons of fun.
November 5, 2024
Trump won the election. But on the bright side....
The Sun is slowly getting brighter, and in about a billion years its luminosity will be 10% higher than today. This will evaporate enough water to create a strong greenhouse effect, which will heat the Earth even more, leading to a feedback loop that eventually evaporates all the oceans and creates a thick cloud layer.
The temperature will rise to 47 °C. There may still be water near the poles, and there may be occasional rainstorms, but most of the Earth will become a desert, with large dune fields covering its equator, and salt flats on what was once the ocean floor.
At this point a lot of water will be in the stratosphere, where ultraviolet light from the Sun breaks down water molecules into hydrogen and oxygen. Hydrogen is very light, so it will gradually escape the atmosphere. All the Earth's seawater will be gone by 1.5 billion years from now.
With no water to serve as a lubricant, plate tectonics will likely stop. Some microbes will survive, such as those already adapted to high temperatures, and life might even find refuge in the atmosphere. However, by 3 billion years all life may go extinct, with the last organisms living underground.
Four billion years from now, the continued brightening of the Sun will heat the Earth's surface enough to melt it. When the Sun switches from burning hydrogen within its core to burning hydrogen in a shell around its core, it will start to expand. By about 12 billion years it should be 3000 times brighter than now.
As this happens, the Earth's temperature will rise to 2000 °C. Most of the atmosphere will be lost to space, and the surface will be a lava ocean.
And nobody will complain.

We can't expect he'll surround himself with people who will restrain him. The Senate and probably the House will be controlled by people under his thumb. The Supreme Court, three of whose members he appointed, has already announced he'll have wide powers to act without being legally liable. He's lining up a cabinet full of billionaires.
My worries are not for my family. We planned ahead and are ready to move to Scotland. My worries are for the US, Ukraine, democracy worldwide, and the biosphere.
We need to organize to resist Trump's bad ideas and criminality. Unfortunately I am not good at politics. So, just a couple of thoughts:
The Democratic Party needs to figure out what it's doing wrong. Many Americans are desperate. 50% live paycheck to paycheck all the time. 25% have negative net worth: they owe more than they own. If Democrats don't take this seriously, people will keep voting for demagogues.
I wish there were a serious constituency for constitutional change:
abolishing the electoral college, introducing ranked choice voting,
banning campaign contributions and other forms of pay-to-play
politics, etc. I don't see how these changes have a chance in the
current environment. How can we improve the overall framework when
politics devolves to a culture war, a battle between two dominant
parties, a plutocracy — or actually all of the above? How could
a new party devoted to true reform gain power? Time for me to study
more history.
November 7, 2024
I love reading about the medieval physics: you can see people struggling against mental traps, often failing, but still putting up a fight. We shouldn't laugh at them: theoretical physicists may be stuck in their own traps today! Good new ideas often seem obvious in retrospect... but only in retrospect.
For example: Aristotle argued that a vacuum is impossible, because the velocity of an object equals the force on it divided by the resistance of the medium it's moving through. A vacuum offers no resistance—so an object would move through it at infinite speed!
Around 1100, the medieval Arab physicist Ibn Bajja disagreed. He argued that the celestial spheres—i.e. the planets and stars — move at finite speeds even in the vacuum. So, he said, we should subtract the resistance of the medium from the object's natural speed, not divide by it.
Averroes fought back, agreeing with Aristotle. Later, Thomas Aquinas sided with Ibn Bajja (who was known in Latin as Avempace). By the 1300s, most Western natural philosophers had sided with Aristotle.
There are definitely problems with the subtraction theory. What if the resistance exceeds the force? Does the object move backwards? But back then they didn't know about negative numbers! So maybe proponents of the subtraction theory would say an object stands still if you push on it with insufficient force to overcome the resistance.
All this reached a pinnacle of complexity in Thomas Bradwardine's 1328 Treatise on the Ratios of Speeds in Motions. He analyzed four theories and then proposed his own. Though he didn't phrase it this way, it seems he argued that speed is proportional to the logarithm of the force over resistance. For example if you cube the ratio of force to resistance, you triple the object's speed.
This theory, which came to be called 'Bradwardine's rule', seems terrible to me. It doesn't solve the problem of infinite speeds in a vacuum, and it says some force is required just to hold an object still. In fact, I hope I'm misinterpreting this theory! But anyway, it caught on: without any experimental evidence backing it up, it took root and was popular for about 100 years.
In Oxford, Richard Swineshead and John Dumbleton applied Bradwardine's rule to solve 'sophisms', the logical and physical puzzles that were starting to become important at Merton College. A bit later this rule appeared in Paris, in the works of Jean Buridan and Albert of Saxony. By the middle of the 1300s it caught on in Padua and elsewhere. And Swineshead, nicknamed The Calculator, used it to study whether a body acts as a unified whole or as the sum of its parts. He imagined a long, uniform, heavy body falling in a vacuum down a tunnel through the center of the earth. Somehow he concluded that it would take an infinite time to reach the center. Don't ask me how—I don't know! But anyway, he rejected this conclusion as unphysical.
So, a lot of struggles!
While the theories I just explained sound pretty bad, something good was happening throughout these arguments: researchers were figuring out the concept of 'instantaneous velocity': the velocity of an object at an instant of time. They didn't define it using derivatives, but it seems getting a good intuitive handle on this was a prerequisite for later work on derivatives.
And Nicole Oresme, trying to formulate Bradwardine's rule in full generality, was led to study fractional powers for the first time! Nobody knew about logarithms back then, so Bradwardine's rule actually said that if you have two objects feeling forces \(F_i\) and encountering resistances \(R_i\), their velocities \(V_i\) are related by $$ \displaystyle{ \frac{F_2}{R_2} = \left(\frac{F_1}{R_1}\right)^{V_2/V_1} }$$ This is simple enough when the ratio \(V_2/V_1\) is a positive integer, but Oresme extended it to fractions!
So, fundamentally misguided physics can still lead to good mathematics. (I will not attempt to draw any lessons for the present.)
I got most of this material from here:
Medieval scientists were deeply confused about the connection between force and velocity: it took Newton to realize force is proportional to acceleration. But in the early 1300s, a group of researchers called the Oxford Calculators made huge progress in understanding objects that move with changing velocity. That was an incredibly important step.
You see, Aristotle had only defined velocity over an interval of time, as the change in position divided by the change in time. But the Oxford Calculators developed the concept of instantaneous velocity, allowing them to discuss objects with changing velocity — and even the concept of acceleration!
That's really cool. But it gets better. The Oxford Calculators made their students write essays on 'sophisms', meaning puzzles or paradoxes. Some of these were logical or philosophical, others physical. And in 1335, one of Oxford Calculators named William Heytesbury wrote a book called Rules for Solving Sophisms. This gives us a hint as to what these puzzles were like — though it's more of a theoretical monograph than a practical how-to book, so we can't really tell what the students were expected to do.
This book has a very interesting section on physics. Here Heytesbury states something called the Mean Speed Theorem. This says that if an object's velocity is changing at a constant rate over some period of time, it goes just as far as if it were moving uniformly with the velocity it had at the middle instant of its motion!
We can think of this as a step toward integrating linear functions. Later in the 1300s, in Paris, Nicole Oresme, gave a clear picture proof of the Mean Speed Theorem. For example, he pointed out that the triangle ACG below has the same area as the rectangle ACDF:
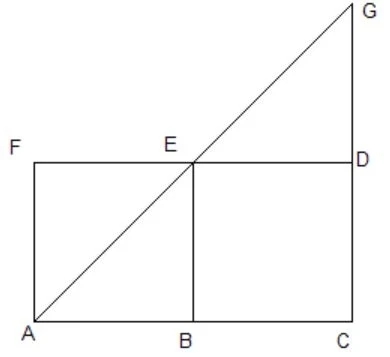
This handles the Mean Speed Theorem for an object starting with zero velocity — an important special case which Heytesbury also found interesting.
Heytesbury's Rules for Solving Sophisms also has some pictures:

But when it comes to the Mean Speed Theorem I haven't seen him giving a picture proof. Instead, he gives a complex purely verbal argument. It's so complicated I haven't managed to follow it yet. I tried, but I gave up: it involves comparing the motion of four different objects. You can see the argument here, starting on page 122:
I managed to find this book in the bowels of my university library, in one of those electronically movable stacks that makes me worry some evil denizen of the nether reaches is going to crush me:

But I'm pleased to report that the tireless criminals of Library Genesis have made this book available to the world in electronic form, so you don't have to take such risks. If you can understand Heytesbury's argument, please explain it to me!
Who were the Oxford Calculators, exactly? They were a group of thinkers associated to Merton College in Oxford. Thus, they're also called the Merton School. Here are the four most important:
If you want to dig deeper into this subject, the place to go is here:
It's a sourcebook, with a lot of important texts translated into English, but it also has long sections explaining the history and the ideas. Note that both books I recommended today were published by the University of Wisconsin in the late 1950s and early 1960s. Maybe they were a powerhouse in medieval physics at that time?
Anyway, I find this stuff fascinating. One obvious question is: why did the Oxford Calculators sort of fizzle out after 1350? Why did it take until 1589 for Galileo to announce that falling bodies actually move in a way described by the Mean Speed Theorem?
There are a lot of possible reasons, but one is hinted at by Thomas Bradwardine's death in 1349. The bubonic plague killed about one third of the population of Europe from 1346 to 1353!
November 9, 2024
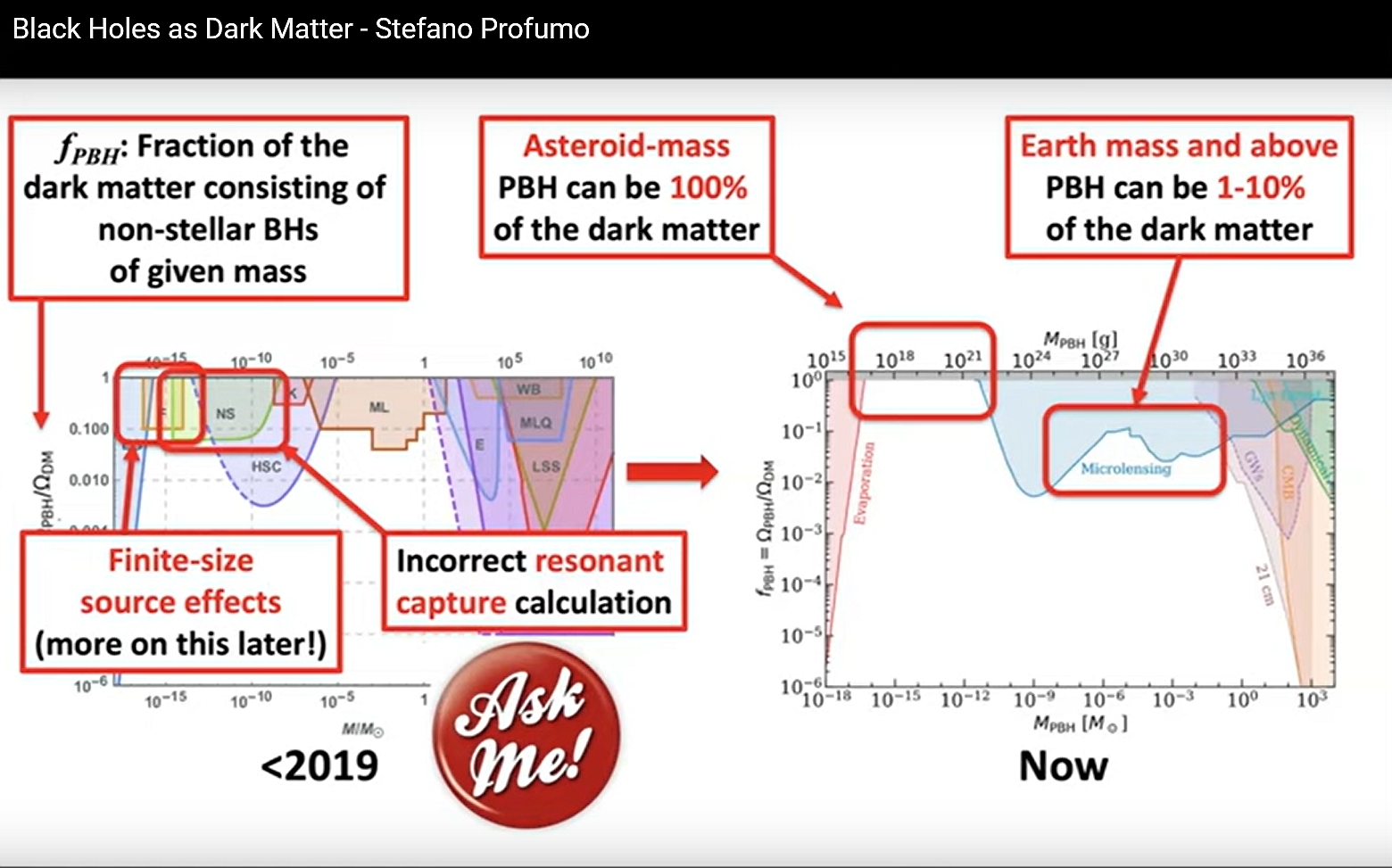
For decades, astrophysicists have been saying dark matter can't be mostly black holes. But this may be wrong: new calculations suggest up to 100% of dark matter could be black holes, about as heavy as asteroids, that formed in the very early universe.
Beware: nobody knows how these 'primordial black holes' would be formed, and nobody has ever seen one! So what's new?
Physicists had done many calculations claiming to rule out black holes of various different kinds as dark matter. For example, dark matter can't be mainly black holes of Earth mass or heavier, since their gravity would focus light as they move in front of stars — and we've looked really hard and haven't seen many of these 'microlensing' events. It also can't be extremely light black holes, because Hawking showed these would explode, and we haven't seen that.
In fact, physicists argued there's no way black holes in any mass range could account for most of the dark matter!
But recently I decided to watch YouTube videos from the Institute of Advanced Studies while pedaling the exercise bike at the gym, to make me look more intellectual, so tough guys won't pick on me.
And I saw a great talk by Stefano Profumo claiming that some of these arguments were wrong! He and his coauthors argue that black holes with masses between \(10^{17}\) and \(10^{22}\) grams are not ruled out: they could in theory account for all the dark matter. I had to look it up: the biggest asteroid, Ceres, has a mass of \(10^{24}\) grams. So these are like small asteroid masses.
He also talks about ways to search for such black holes!
Above you see the old limits on primordial black holes in different mass ranges... and the new ones.
Here is Stefano Profumo's talk on the possibility of black hole dark matter. The graphs above appear at 13:27.
Here is a paper about this stuff:
When I was a kid, under the influence of science fiction, I once dreamt I was going to the moon. It was so exciting! When I woke up I was crushed. Later, when I grew up, I realized sending humans into space is a waste of money at present — though it was good to prove we could do it.
If we're serious about exploring airless environments with lots of radiation, we should be developing cyborgs and better AI. But meanwhile, we can explore space from the comfort of home using space probes and telescopes. We just need to get better at explaining to ordinary folks how cool this is. I can get thrilled by graphs and tables of data, because I can vividly imagine what they mean. Most folks would prefer a good animated video.
MeerKAT is an amazing array of 64 radio telescopes in South Africa. Astronomers want to expand this to the Square Kilometer Array, which will actually consist of thousands of telescopes in South Africa and Australia. But it's already seeing great stuff. For example, this June they found a weird thing that flashes like a pulsar, but extremely slowly: roughly once an hour, instead of many times a second like an ordinary pulsar!
That's insane! What is this thing? We don't know, and that's exactly why it's cool.
Imagine an enormous star flinging off its outer layers after it runs out of fuel and its core collapses under its own gravity. If the core doesn't collapse to form a black hole or completely explode, it can shrink down to a ball of neutronium just 20 kilometers across. Just as a ballerina spins faster as she pulls in her arms, this ball spins really fast — like 1000 rotations a second. And since neutronium conducts electricity, it can blast out radio waves as it spins, creating a blinking radio signal, called a pulsar.
Pulsars are so precisely periodic that when Jocelyn Bell first spotted one, she considered the possibility that it was a signal from space aliens!
We did not really believe that we had picked up signals from another civilization, but obviously the idea had crossed our minds and we had no proof that it was an entirely natural radio emission. It is an interesting problem — if one thinks one may have detected life elsewhere in the universe, how does one announce the results responsibly?
Like the rest of us, pulsars slow down as they age. But this also means their signal weakens, and eventually quits. So we usually don't see pulsars in the gray region of the following chart — to the right of the line called the 'pulsar death line'.
Pulsars are the gray dots to the left of this line. The pink squares are called 'magnetars’. These are the squalling infants in the world of pulsars: young and highly magnetized neutron stars that do crazy stuff like put out big bursts of X-rays now and then.
But then there are weirder things. In Australia there's an array called Australian Square Kilometer Array Pathfinder or ASKAP, which was built to test technologies for the forthcoming Square Kilometer Array. It was searching for radio waves connected to a gamma ray burst in 2022 when it stumbled on something that blasts out radio waves about once an hour. It lost track of this object, so folks brought in the more powerful MeerKAT array and found it again.
Now this mysterious radio source is called ASKAP J1935+2148. It's well to the right of the pulsar death line. What could it be?
It blasts out radio waves once every 54 minutes, which is incredibly slow for a pulsar. Pulsars usually pulse somewhere between 1000 times a second and once every few seconds.
ASKAP J1935+2148 puts out three kinds of pulses in a seemingly random way:
It could be a really weird pulsar, but nobody knows how a pulsar spinning so slowly could put out radio waves. It could be a pulsar-like white dwarf. Three of these are known, people argue about how they work, and they pulse more slowly than ordinary pulsars — but not as slowly as this.
In short, it's a mystery! And that means we'll learn something cool.
For a nice account of this, try Astrobites:
For even more details, try the original paper:
That's where the nice figure of the 'pulsar death line' came from.
November 29, 2024
I didn't know that wolves can pollinate plants.
This is an Ethiopian wolf, the most endangered predator in Africa. These wolves like to lick sweet nectar off a flower called the Ethiopian red hot poker. And as they go from flower to flower, their muzzles get dusted with pollen! So while it's not yet proved that these wolves are important as pollinators, it seems awfully likely.
Scientists think these wolves don't get much of their caloric intake from this nectar. The "dessert hypothesis" says the wolves just like the taste!
For more, check out this open-access paper: