
The world's expert on snowflakes has written a 540-page book on them. Now he's giving it away for free here:
Condensed matter physics is so cool! Bounce 4 laser beams off mirrors to make an interference pattern with 8-fold symmetry. Put a Bose–Einstein condensate of potassium atoms into this 'optical lattice' and you get a superfluid quasicrystal! But that's not all....
As you increase the intensity of the lasers, the Bose-Einstein condensate (in blue) suddenly collapses from a quasicrystal to a 'localized' state where all the atoms sit in the same place!
Here the gray curve \(V_0\) is the potential formed by the lasers, while the blue curve \(\psi_0\) is the wavefunction of the Bose–Einstein condensate:
When \(V_0\) exceeds a certain value, localization occurs. For more, see:
An 'optical vortex' is a beam of light that turns like a corkscrew as it moves. It's dark at the center.
You can use an optical vortex to trap atoms! They move along the dark tube at the center of the vortex.
Photons have spin angular momentum, and in circularly polarized light this equals +1 or -1. An optical vortex is different: it exploits the fact that photons can also have orbital angular momentum! This can be any integer \(m\), as shown above.
So, some hotheads call an optical vortex a 'photonic quantum vortex'. But you can study optical vortices without quantum mechanics, using the classical Maxwell equations! The electromagnetic field is described using a complex function that in cylindrical coordinates is \(\exp(im\theta)\) times some function that vanishes at \(r = 0\): the dark center. One class of functions like this are the 'hypergeometric-Gaussian modes':
Rather complicated! More importantly, the phase of the electromagnetic field, \(\exp(im\theta)\), is undefined at the center of the optical vortex. It turns around \(m\) times as you go around the vortex. So this number \(m\) has to be an integer. It's a simple example of a 'topological charge'.
People make optical vortices using many different technologies,
including spiral-shaped pieces of plastic, 'computer-generated
holograms', and computer-controlled liquid crystal gadgets called
''.
February 6, 2020
What's the difference between a polaron and a polariton?
When an electron moves through a crystal, it repels other electrons and attracts the protons. The electron together with this cloud of distortion acts like a particle in its own right: a 'polaron'.
A polariton is more complicated.
First, when an electron in a crystal is knocked out of place, it leaves a 'hole'. This hole can move around — and it acts like a positively charged particle!
Since electrons are negative and holes are positive, they attract each other! An electron orbiting a hole acts like a hydrogen atom. It's called an 'exciton'. It can move around! But after a while, the electron falls into the hole.
Finally, an exciton can attract a photon! They can stick to each other a form a new particle called a 'polariton'!
Polaritons are exciting to me because they're made of an electron, an absence of an electron, and light. Here's the dispersion relation (the relation between energy and moment) for polaritons as compared with that for photons and excitons.
You'll notice there are two kinds of polaritons. These form another
basis of the space of quantum states spanned by the photon and exciton.
February 7, 2020
Scientists have made 'liquid light' by blending light and matter. It can be superfluid and flow smoothly past an obstacle (left), or an ordinary fluid that forms eddies as it flows past (middle), or it can form a sonic boom (right).
That's right: a sonic boom in liquid light!
As I explained on February 6, a polariton is a particle that's a blend of light and matter. More precisely, it's a quantum superposition of a photon and an exciton, which is an electron-hole pair.
Scientists made a fluid of polaritons! Then they made it flow. The polaritons only last for 4-10 picoseconds (trillionths of a second). But that was long enough to watch the fluid do all the usual things fluids do: turbulence, sonic booms, etc.
Try my blog for more:

You can effectively manage to adjust the mass of photons by trapping it between two parallel mirrors. Its frequency in the transverse direction affects its energy as if it had a mass. Now you have a massive photon in 2 dimensions!
This lets you do some interesting things.

To get your massive photons to interact, you should get them to interact strongly with the material between your parallel mirrors.

The quotes are from this absolutely delightful article:
A 'topological insulator' is insulating on the inside, but its surface conducts electricity. More importantly, electrons on the surface have their spin locked at right angles to their momentum, so they come in two kinds.
(This is the simplest type of topological insulator — there are others.)
So far, most topological insulators have been made with bismuth compounds like Bi2Se3 and Bi2Te3. Someday they may have applications in 'spintronics': a version of electronics where information is encoded in electron spins. A spin, after all, is nature's own qubit!
But right now, a lot of interest in topological insulators comes from the math. Their classification, the 'tenfold way', unifies the 8 types of real and 2 types of complex Clifford algebras! For more about it, read this:
Condensed matter physicists are exciting. They're exciting electrons, knocking them out of their usual places in crystals, leaving holes. The electrons and holes orbit each other, forming 'excitons'.
They've been trying to make a metal out of excitons: 'excitonium'!
When a hole is much heavier than an electron, it stands almost still when an electron orbits it. So, they form an exciton that’s very similar to a hydrogen atom!
Hydrogen comes in many forms. At high densities, like the core of Jupiter, it becomes a metal.
Any ideas?
In 1978 the Russian physicist Abrikosov wrote a short and very creative paper in which he raised the possibility that excitons could form a crystal similar to metallic hydrogen! He called this new state of matter 'metallic excitonium'.
Can we actually make it? I don't think anyone has made metallic excitonium yet — correct me if I'm wrong. But in 2016, researchers made something equally exciting! An electron is a fermion and so, therefore, is a hole. Two fermions make a boson — so an exciton is a boson.
Any ideas?
At low temperatures, identical bosons like to be in the exact same state. This is called a 'Bose-Einstein condensate'. And in 2016, researchers made a Bose-Einstein condensate of excitons! At shockingly high temperatures, too.
Here's the paper:

Max Planck was the first established physicist to embrace Einstein's work on special relativity. He worked out some important consequences.
His formula for momentum almost matches Newton's for speeds much slower than light. But it gives dramatically different answers at high speeds.
Planck published the paper containing this formula shortly after a physicist named Walter Kaufmann had done experiments that seemed to confirm a different formula for momentum, due to Max Abraham! But Planck wrote:
However, in view of the complicated theory of these experiments I would not completely exclude the possibility, that the principle of relativity on closer elaboration might just prove compatible with the observations.You can read his paper, translated into English, here:
It's short and sweet. Equation 6) contains the new formula for momentum, built into the new relativistic version of Newton's \(F = dp/dt\).
Later, in 1914, Planck helped Einstein get a research position in Berlin.
February 21, 2020

In 1907 Einstein tried to combine special relativity with gravity — and very soon he realized gravity would make clocks tick slower, and would bend light.
It took him until 1915 to find the equations of general relativity. He needed the right kind of math.
In 1912 an old college friend, a mathematician named Marcel Grossman, helped Einstein get a job in Zurich. That year, Grossman told Einstein that the math he needed for describing gravity had been invented by Riemann. He warned Einstein that it was a "terrible mess".
Grossman was not an expert on Riemannian geometry, but he and Einstein quickly learned the subject together. They came out with a paper applying it to gravity in 1913.
They ran into a big problem, though, which Einstein only surmounted later. They realized: if the equations of gravity are 'generally covariant' — preserved by all coordinate transformations — you cannot use complete knowledge of what's happening at \(t = 0\) to predict what will happen at a point in the future with specific coordinates \((t,x,y,z)\). After all, a coordinate transformation could change the coordinates of that point to some other coordinates \((t',x',y',z')\). Nature can't guess what coordinates you are using!
Einstein and Grossman erroneously concluded that the equations of gravity should not be generally covariant. Only later did Einstein realize that they should be!
It turns out to be okay that we can't predict what will happen at a point with coordinates \((t,x,y,z)\). All a theory needs to predict is what we can observe. Coordinates are not something we observe.
This realization freed Einstein, and he found the correct equations of
general relativity on November 25, 1915. It was still a long road to
our current understanding of black holes, the Big Bang and
gravitational waves. But that's another story.
February 26, 2020
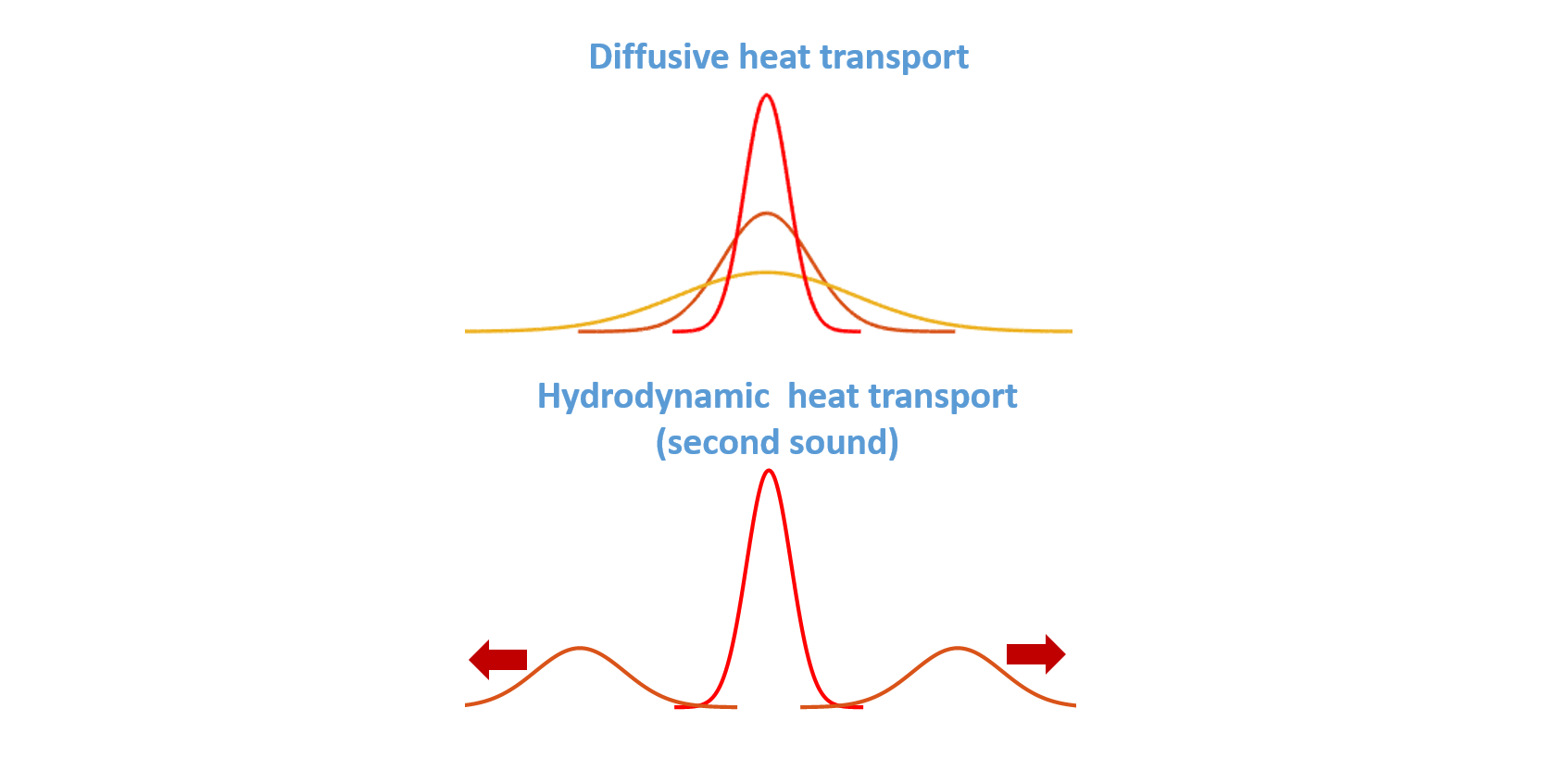
What's even cooler than sound? Second sound!
Usually heat spreads out like the picture on top. Second sound when heat moves in waves.
You see, ordinary sound — 'first sound' — is waves of pressure. 'Second sound' is waves of temperature.
Liquid helium is a mix of normal liquid and superfluid. In ordinary sound in liquid helium, a wave of high pressure has more of both normal liquid (n) and superfluid (s):
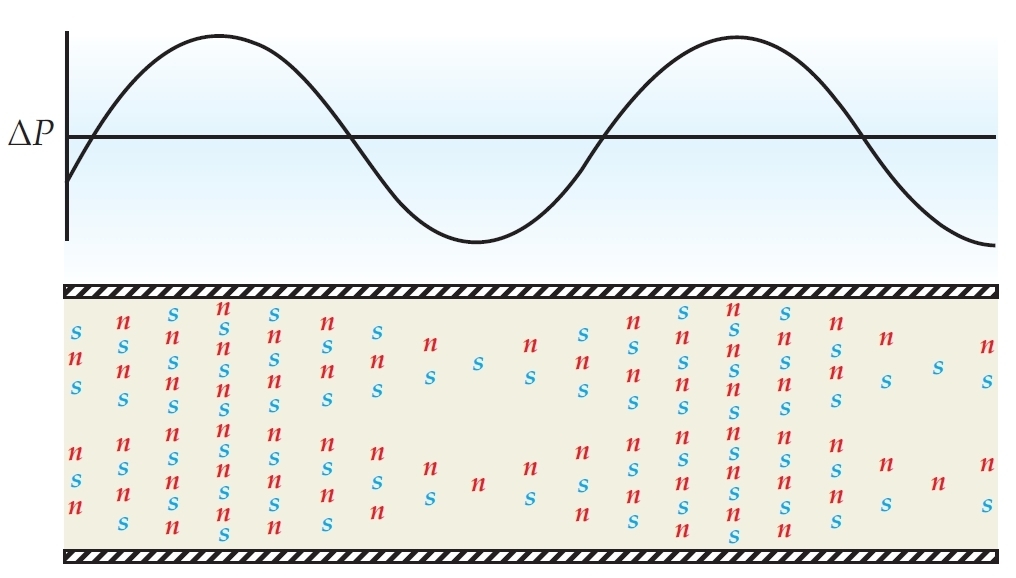
But in second sound, a wave of high temperature has more normal fluid and less superfluid. The total pressure is constant:
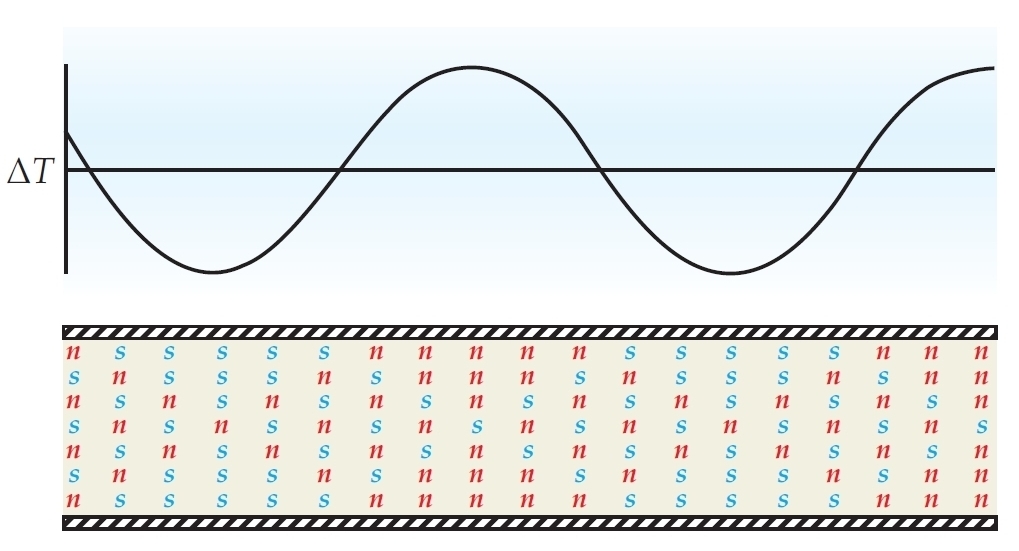
Here's a great introduction to second sound in liquid helium:
Define a "time-dependent set" to be a set \(X(n)\) for each natural number \(n\), together with functions \(X(n) \to X(n+1)\).
For example, \(X(n)\) could be the set of solutions to some equation that you know on the nth day of your research.
As days pass you can find new solutions, and also prove that two solutions you knew are actually equal. You can never lose solutions, or discover that two solutions you thought were equal are different. So this is a simple model of an infallible but not omniscient mathematician.
There is a category of time-dependent sets, and it's a topos. This means you can do all of mathematics and logic in this category — like you can with sets. But logic works differently in the topos of time-dependent sets, because you learn new truths as time goes on!
Instead of a mere set of truth values, $$ \{\mathrm{true}, \mathrm{false}\}$$ there's a time-dependent set of truth values, called \(\Omega\). For each time \(n\), \(\Omega(n)\) has infinitely many elements: known today, known tomorrow, known the next day, etc.,... and never known.
In my article, I don't yet say much about how logic works with time-dependent truth values — like why the law of excluded middle fails. Instead, I show how to derive time-dependent truth values from the category of time-dependent sets.
In previous articles I explained why any presheaf category is a topos and how to figure out the truth values in such a category. Here I'm illustrating how that works for time-dependent sets.
Later I'll get into Heyting algebras and the law of excluded middle!
February 29, 2020
Condensed matter physics is so full of surprises. I am constantly
awed by it. I just learned:
You can make particles that act like massless particles moving at the speed of light when they move in one direction — but like massive particles that move slower than light when they move in the orthogonal direction!
In classical mechanics, at low momenta, ignoring relativistic effects, the energy of a massive particle grows quadratically with the magnitude of its momentum: $$ E = \frac{p^2}{2m} $$ where \(m\) is the particle's mass.
This doesn't make sense for a particle of mass zero. That's because a massless particle moves at the speed of light and we need special relativity to understand it. In special relativity, the energy of a massless particle depends in a very different way on its momentum: it grows linearly with the magnitude of the momentum! More precisely, $$ |E| = c |\vec{p}| $$ where \(c\) is the speed of light.
All these formulas are still true in quantum mechanics, but we have more.
In quantum mechanics, energy is proportional to the rate at which the wavefunction wiggles in time: that is, its frequency \(\omega\). Similarly, momentum is proportional to the rates at which the wavefunction wiggles in the 3 spatial directions: that is, its wave vector \(\vec{k} = (k_x, k_y, k_z)\). In both cases the constant of proportionality is Planck's constant: $$ E = \hbar \omega, \quad \vec{p} = \hbar \vec{k} $$ We can combine these our earlier formulas. The result is that at low momenta, ignoring relativistic effects, the frequency of the wavefunction of a massive particle is a quadratic function of the magnitude of the wave vector: $$ \omega = \hbar \frac{k^2}{2m} $$ but for a massless particle, the frequency depends linearly on the magnitude of the wave vector, or more precisely $$ |\omega| = c |\vec k| $$
So that's how massive and massless particles are different. But you can make the energy of a photon, or electron, or a quasiparticle of your choice, be almost any function of its momentum if you're good enough at making strange materials. The reason is that its effective energy and momentum depend on its interactions with the material.
So, if you're clever enough, you can make the relation between energy and momentum look like this:
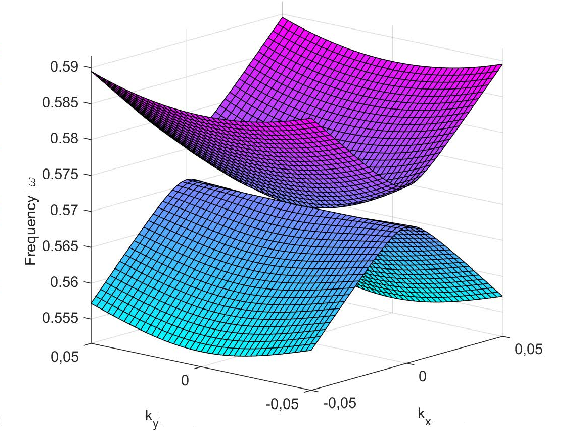
Note that if you set \(k_y\) to zero you get $$ |\omega| \propto k_x^2 $$ like a massive particle at low momentum, except that \(\omega\) takes both signs. But if you set \(k_x\) to zero you get $$ |\omega| \propto |k_y| $$ like a massless relativistic particle.
The relation between a particle's frequency and its wave vector is called its dispersion relation. The unusual dispersion relation in the picture above is called a 'semi-Dirac cone'.
One way to create a semi-Dirac cone is described here:
Wu created a photonic crystal consisting of square array of elliptical cylinders of plastic with a high dielectric constant in air. But in condensed matter physics there are other very different ways to make dispersion relations with semi-Dirac cones.
Wu's paper is here: