The Tenfold Way

John Baez

November 22, 2020

There are 10 of each of these things:

I'll summarize how it works, and then you can read these for more:

I've written a terse summary of the simplest mathematical ideas: I've also given a talk on this stuff, and you can see my slides and watch a video. But that talk doesn't cover everything in here!

I'll start by explaining the origin of this subject in physics, and then move on to more mathematical aspects.

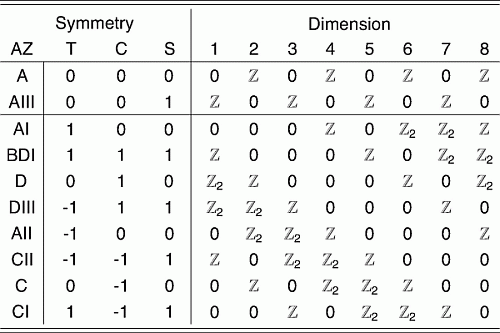
Ten kinds of matter

The idea of the ten-fold way goes back at least to 1996, when Altland and Zirnbauer discovered that substances can be divided into 10 kinds.

The basic idea is pretty simple. Some substances have time reversal symmetry: they would look the same, even on the atomic level, if you made a movie of them and ran it backwards. Some don't — these are more rare, like certain superconductors made of yttrium barium copper oxide! Time reversal symmetry is described by an antiunitary operator \(T\) that squares to \(1\) or to \(-1\): please take my word for this, it's a quantum thing. So, we get 3 choices, which are listed in the chart under \(T\) as \(1, -1\), or \(0\) (no time reversal symmetry).

Similarly, some substances have charge conjugation symmetry, meaning a symmetry where we switch particles and holes: places where a particle is missing. The 'particles' here can be rather abstract things, like 'phonons' — little vibrations of sound in a substance, which act like particles — or 'spinons' — little vibrations in the lined-up spins of electrons. Basically any way that something can wave can, thanks to quantum mechanics, act like a particle. And sometimes we can switch particles and holes, and a substance will act the same way!

Like time reversal symmetry, charge conjugation symmetry is described by an antiunitary operator \(C\) that can square to \(\pm 1\). So again we get 3 choices, listed in the chart under \(C\) as \(1, -1\), or \(0\) (no charge conjugation symmetry).

So far we have \(3 \times 3 = 9\) kinds of matter. What is the tenth kind?

Some kinds of matter have neither time reversal nor charge conjugation symmetry, but they're symmetrical under the combination of time reversal and charge conjugation! You switch particles and holes and run the movie backwards, and things look the same!

In the chart they write \(1\) under the \(S\) when your matter has this combined symmetry, and \(0\) when it doesn't. So, "\(0 0 1\)" is the tenth kind of matter (the second row in the chart).

This is just the beginning of an amazing story. Since then people have found substances called topological insulators that act like insulators in their interior but conduct electricity on their surface. We can make 3-dimensional topological insulators, but also 2-dimensional ones (that is, thin films) and even 1-dimensional ones (wires). And we can theorize about higher-dimensional ones, though this is mainly a mathematical game.

So we can ask which of the 10 kinds of substance can arise as topological insulators in various dimensions. And the answer is: in any particular dimension, only 5 kinds can show up. But it's a different 5 in different dimensions! This chart shows how it works for dimensions 1 through 8. The kinds that can't show up are labelled 0.

If you look at the chart, you'll see it has some nice patterns. And it repeats after dimension 8! In other words, dimension 9 works just like dimension 1, and so on.

If you read some of the papers I listed, you'll see that the \(\mathbb{Z}\)'s and \(\mathbb{Z}_2\)'s in the chart are the homotopy groups of the ten classical series of compact symmetric spaces. The fact that dimension \(n+8\) works like dimension \(n\) is called Bott periodicity.

Furthermore, the stuff about operators \(T\), \(C\) and \(S\) that square to 1, -1 or don't exist at all is closely connected to the classification of associative real super division algebras. So, it all fits together.

Super division algebras

In 1996, as part of an Institute for Advanced Studies program on quantum field theory, Pierre Deligne wrote some notes on spinors which included a classification of the associative real super division algebras: that is, finite-dimensional associative real \(\mathbb{Z}_2\)-graded algebras having the property that every nonzero homogeneous element is invertible. Later this classification was very tersely handled in Todd Trimble's paper on the super Brauer group and super division algebras. Some of the key ideas are much older: But I really enjoyed Todd's effortless proof.

At the time I didn't think much about how there are exactly 10 of these guys. Now this turns out to be a big deal.

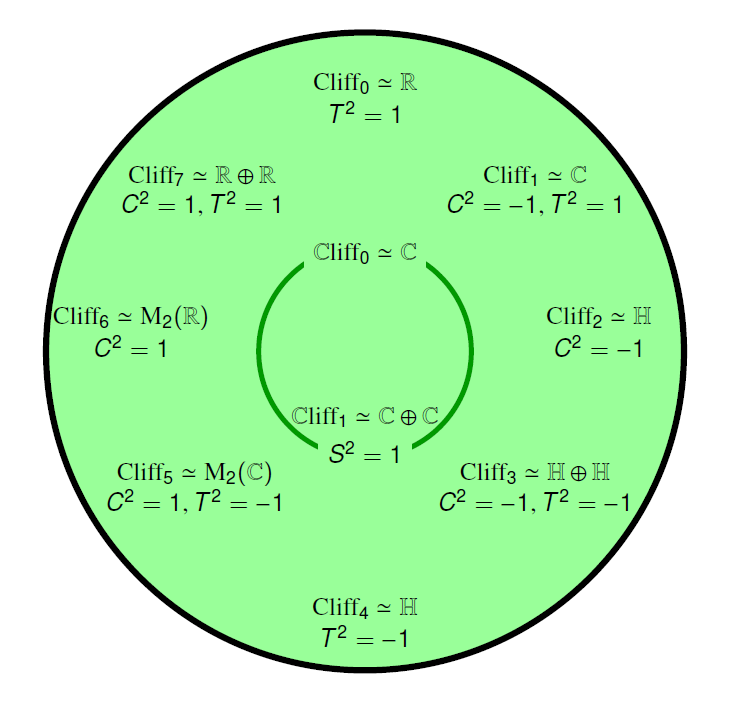
3 of them are purely even, with no odd part: the usual division algebras \(\mathbb{R}, \mathbb{C}\) and \(\mathbb{H}\).

7 of them are not purely even. Of these, 6 are Morita equivalent to the real Clifford algebras \(\mathrm{Cl}_1, \mathrm{Cl}_2, \mathrm{Cl}_3, \mathrm{Cl}_5, \mathrm{Cl}_6\) and \(\mathrm{Cl}_7\). These are the super algebras generated by 1, 2, 3, 5, 6, or 7 odd square roots of -1.

Now you should have at least two questions:

Representations of Clifford algebras are used to describe spin-1/2 particles, so it's exciting that 8 of the 10 associative real super division algebras are Morita equivalent to real Clifford algebras.

But I've already mentioned one that's not: the complex numbers, \(\mathbb{C}\), regarded as a purely even algebra. And there's one more! It's the complex Clifford algebra \(\mathbb{C}\mathrm{l}_1\).

Let me explain. In general, the complex Clifford algebra \(\mathbb{C}\mathrm{l}_n\) is defined to be the complex super algebra you get by taking the purely even algebra \(\mathbb{C}\) and throwing in \(n\) odd square roots of -1. So, \(\mathbb{C}\mathrm{l}_1\) is \(\mathbb{C} \oplus \mathbb{C}e\) where \(e\) is an odd element with \(e^2 = -1\).

And as soon as you think about this, you'll notice that the purely even algebra \(\mathbb{C}\) is \(\mathbb{C}\mathrm{l}_0\). In other words, it's the super algebra you get by taking the purely even algebra \(\mathbb{C}\) and throwing in no odd square roots of -1.

So, in fact all 10 real super division algebras are Morita equivalent, as super algebras, to either real or complex Clifford algebras!

Even better, every real or complex Clifford algebra is Morita equivalent to a real super division algebra.

More connections

At this point things start fitting together:

Meanwhile, the purely even \(\mathbb{R}, \mathbb{C}\) and \(\mathbb{H}\) underlie Dyson's 'three-fold way', which I explained in detail here:

Briefly, if you have an irreducible unitary representation of a group on a complex Hilbert space \(H\), there are three possibilities:

In physics applications, we can take \(J\) to be either time reversal symmetry, \(T\), or charge conjugation symmetry, \(C\). Studying either symmetry separately leads us to Dyson's three-fold way. Studying them both together leads to the ten-fold way!

So the ten-fold way seems to combine in one nice package:

I could throw 'the complex Brauer group' into this list, because that's lurking here too, but it's the trivial group, with \(\mathbb{C}\) as its representative.

The ten associative real super division algebras

Just for the record, here are all 10 associative real super division algebras. 8 are Morita equivalent to real Clifford algebras. In fact, all 8 of these are real Clifford algebras if we expand the definition a bit. I've talked about \(\mathrm{Cl}_n\), which is the free superalgebra on \(n\) anticommuting square roots of \(-1\). But let's define \(\mathrm{Cl}_{-n}\) to be the free superalgebra on \(n\) anticommuting square roots of \(+1\). This is nice because with this definition it's still true that adding 8 to the index of our Clifford algebra gives a Morita equivalent superalgebra. We write this as $$ \mathrm{Cl}_{n+8} \simeq \mathrm{Cl}_n. $$ And we have these 8 super division algebras:

Since \(\mathrm{Cl}_{n+8}\) is Morita equivalent to \(\mathrm{Cl}_n\) both for positive and negative \(n\), we can stop here if we're just looking for Morita equivalence classes, and there also happen to be no more super division algebras down this road.

The remaining 2 real super division algebras are complex Clifford algebras:

In the last one we could also say "with \(e^2 = 1\)": we'd get something isomorphic, not a new possibility.

Ten kinds of matter, revisited

What does all this stuff about Clifford algebras and super division algebras have to do with Altland and Zirnbauer's classification of substances into 10 kinds? We are now in a position to see how this works!

We start with a complex Hilbert space that may (or may not) have some operators on it called \(T, C\) and \(S\). \(T\) stands for time reversal, \(C\) stands for charge conjugation, and \(S\) stands for the combination of charge conjugation and time reversal, which may be a symmetry even when \(C\) and \(T\) are not both symmetries. Below we write \(= 0\) to mean that one of these three possible symmetries is not actually a symmetry of the given kind of substance.

\(T\) and \(C\) are antiunitary, for physical reasons I will not explain here. When you apply them twice, they equal the identity up to a phase, since physically you get back where you started when you reverse the direction of time twice or switch particles and holes twice, but multiplying every state by the same phase has no physically detectable effect. Thus, we have \(T^2 = \alpha\) and \(C^2 = \beta\) for some phases (unit complex numbers) \(\alpha\) and \(\beta\). This implies $$ \alpha T = T^2 T = T T^2 = T \alpha, $$ but because \(T\) is antiunitary we also have $$ \alpha T = T \overline{\alpha}. $$ Thus we have \(\alpha = \overline{\alpha}\), which forces \(\alpha = \pm 1\). In short we must have \(T^2 = \pm 1\) whenever we our substance has time reversal symmetry. The same argument shows \(C^2 = \pm 1\) whenever it has charge conjugation symmetry.

It follows that when we have both \(C\) and \(T\) as symmetries, \(S = CT\) is a unitary operator with \(S^2 = \pm 1\). Indeed we shall assume \(S\) is unitary with \(S^2 = \alpha\) for some phase \(\alpha\) even when it's not really built as the product of symmetries \(C\) and \(T\). But note that since \(S\) is unitary, if \(S^2 = \alpha\) we can redefine \(S\) by dividing it by \(\alpha^{1/2}\) and get \(S^2 = 1\). We will always do this. This does not work for \(C\) and \(T\) because they are conjugate-linear: for example if \(C^2 = \alpha\) for some phase \(\alpha\), then \((C \alpha^{-1/2})^2\) is still \(\alpha\).

Next, given a unitary \(S\) with \(S^2 = 1\), we can always chop the complex Hilbert space it acts on as the direct sum of two subspaces: the part consisting of vectors \(v\) with \(Sv = v\), and the part consisting of vectors \(v\) with \(Sv = -v\). This is important, because it makes our complex Hilbert space \(\mathbb{Z}_2\)-graded! (When we have no operator \(S\) we will think of our Hilbert space as purely even.)

What do the two subspaces mean? It would be nice to think of them as describing 'particles' and 'holes'.

For this interpretation to be reasonable, we want \(C\) to map vectors with \(Sv = v\) to vectors with \(Sv = -v\), and vice versa. At first this seems incorrect, since \(C\) and \(T\) commute, for reasons I don't want to explain here. This implies that \(S = CT\) commutes with \(C\), so that \(C\) maps vectors \(v\) with \(Sv = v\) to other vectors obeying this same equation.

But remember that when we had \(S = CT\) with \(S^2 = -1\) we redefined \(S\), multiplying it by \(i\) to achieve \(S^2 = 1\). In this case, even though our original \(S = CT\) commuted with \(C\), our new \(S = iCT\) will anticommute with it, since \(C\) is antiunitary. So in this case \(C\) will indeed map vectors with \(Sv = v\) to vectors with \(Sv = -v\), and vice versa, just as we want!

When does this happen? It happens when \((CT)^2 = -1\). In other words, it happens when just one of \(C\) or \(T\) squares to \(-1\).

Next we'll see that substances with various kinds of symmetry are described by representations of various Clifford algebras — namely, those that are associative real super division algebras!

Let's start with the 2 super division algebras that are complex Clifford algebras:

Then let's do the 8 real ones. In these cases, unlike the last case, we can always get \(S\) with \(S^2 = 1\) iff we have \(C\) and \(T\) with \(C^2 = \pm 1, T^2 = \pm 1\), simply by taking \(S = CT\) if \((CT)^2 = 1\) and \(S = iCT\) if \((CT)^2 = -1\).

All this information is summarized in the following chart, where \(\simeq\) means 'Morita equivalent to'. Click on the chart to download a PDF that explains things is a bit more detail:

Symmetric spaces

What's the relation to the 10 classical infinite families of compact symmetric spaces? For the full answer to that, I suggest reading Gregory Moore's Quantum symmetries and compatible Hamiltonians. But if you look at this chart by Ryu et al, you'll see these families listed at right in the column "Hamiltonian":

Here's my story about how this stuff works. Each real Clifford algebra \(\mathrm{Cl}_n\) is a '\(\ast\)-algebra'. In other words, for any \(a \in \mathrm{Cl}_n\) there's an element \(a^\ast \in \mathrm{Cl}_n\) such that $$ (a + b)^\ast = a^\ast + b^\ast, \; (ab)^\ast = b^\ast a^\ast $$ and $$ (\alpha a)^\ast = \alpha a^\ast $$ for all \(\alpha \in \mathbb{R}\). The star operation is determined by this: each square root of -1 in \(\mathrm{Cl}_n\), say \(e_i\), has $$ e_i^\ast = -e_i. $$ So, for example, the star operation in \(\mathrm{Cl}_1 = \mathbb{C}\) is just the usual complex conjugation.

Any \(\ast\)-algebra gives a Lie group consisting of the "unitary" elements \(a \in A\), meaning those with $$ aa^\ast = a^\ast a = 1. $$ Thus, Clifford algebras give Lie groups! By the way, these groups are not the Spin groups that Clifford algebras are famously used to construct: those are subgroups of the groups I'm talking about now.

The group of unitary elements in \(\mathrm{Cl}_n\) depends heavily on \(n\) mod 8, thanks to Bott periodicity. We can simplify the story in some ways by taking the limit as \(n \to \infty\) while keeping \(n\) the same mod 8. We then get certain infinite-dimensional Lie groups as follows:

Next, we use the fact that each Clifford algebra sits inside the next one: as an algebra, though not as a superalgebra, \(C_n\) is just the even part of \(C_{n+1}\). So, each of the above groups is a subgroup of the next one, in a way that cycles around mod 8. We can thus take the quotient of each one by the previous one!

For example, after the 7th group \(\mathrm{O} \times \mathrm{O}\) comes the 0th group \(\mathrm{O}\). \(\mathrm{O}(n) \times \mathrm{O}(n)\) sits inside \(\mathrm{O}(n)\) as block diagonal matrices so \(\mathrm{O} \times \mathrm{O}\) is a subgroup of \(\mathrm{O}\). The quotient \(\mathrm{O}/\mathrm{O} \times \mathrm{O}\) is an interesting space: you can think of it as the space of all infinite-dimensional real subspaces of an infinite-dimensional real vector space that's 'twice as big'.

The 'real Grassmannian' \(\mathrm{O}(m+n)/\mathrm{O}(m) \times \mathrm{O}(n)\) is the set of all \(m\)-dimensional subspaces of \(\mathbb{R}^{m+n}\). It's a Riemannian manifold that's so symmetrical that for every point there's a symmetry called inversion about that point, which fixes that point and sends each tangent vector \(v\) to that point to \(-v\). Such a Riemannian manifold is called a symmetric space.

Cartan discovered that there are 10 infinite families of compact symmetric spaces and also 17 exceptions. Here I'm including compact Lie groups, since these really are compact symmetric spaces, even though most people don't include them. For the precise rules behind this classification, go here:

The 10 infinite families are closely connected to the tenfold way! For example, one of these families consists of the real Grassmannians \(\mathrm{O}(m+n)/\mathrm{O}(m) \times \mathrm{O}(n)\), all of which sit in \(\mathrm{O}/\mathrm{O} \times \mathrm{O}\) in a nice way.

Let's see all 10 infinite families of compact symmetric spaces. We get 8 from the real Clifford algebras, in the way I've just described:

The other two infinite families of compact symmetric spaces come from complex Clifford algebras. Complex Clifford algebras are periodic mod 2, in the sense that \(\mathbb{C}\mathrm{l}_{n+2}\) is isomorphic as a super algebra to \(2 \times 2\) matrices with entries in \(\mathbb{C}\mathrm{l}_n\). Thus, the group of unitary elements in \(\mathrm{Cl}_n\) depends heavily on \(n\) mod 2. We can take the limit of these groups by letting \(n \to \infty\) while keeping \(n\) the same mod 2. We then get two infinite-dimensional Lie groups:

\(\mathrm{U}\) sits inside \(\mathrm{U} \times \mathrm{U}\) as the elements of the form \( (g,g) \). \(\mathrm{U} \times \mathrm{U}\) sits inside \(\mathrm{U}\) as the block diagonal matrices. We thus get the remaining two infinite families of compact symmetric spaces:

Cartan gave his 10 infinite families of compact symmetric spaces funny names: A, AI, AII, AIII, BDI, C, CI, CII, D, and DII. People like to use these even though they're a bit hard to remember. You can see how they're related to the groups \(\mathrm{O}, \mathrm{Sp}\) and \(\mathrm{U}\) by looking at Ryu's chart again:

The ten associative real super division algebras, revisited

It's not hard to prove there are exactly 10 associative real super division algebras. You shouldn't be intimidated by this fact, so let's see why it's true! Suppose \(A\) is a real super division algebra. Then its even part \(A_0\) is closed under multiplication, and the inverse of an even element must be even, so \(A_0\) a division algebra. One possibility is that \(A_1 = \{0\}\), and this gives three options: In short, the three real division algebras can be seen as "purely even" super division algebras.

What if \(A_1 \ne \{0\}\)? Then we can choose a nonzero element \(e \in A_1\). Since it is invertible, multiplication by this element sets up an isomorphism of vector spaces \(A_0 \cong A_1\). In the case \(A_0 = \mathbb{R}\), we can rescale \(e\) by a real number to obtain either \(e^2 = 1\) or \(e^2 = -1\). This gives two options:

In the case \(A_0 = \mathbb{C}\), note that the map \(a \mapsto eae^{-1}\) defines an automorphism of \(A_0\), which must be either the identity or complex conjugation. If \(eae^{-1} = a\) then \(e\) commutes with all complex numbers, so we can rescale it by a complex number to make \(e^2\) be any real number we want, say \(e^2 = 1\). If \(eae^{-1} = \overline{a}\) then \(ea =\overline{a}e\), so \(e(e^2) = (e^2)e\) implies that \(e^2\) is real. Rescaling \(e\) by a real number, we can obtain either \(e^2 = 1\) or \(e^2 = -1\). So, we have three options: Finally, in the case \(A_0 = \mathbb{H}\), the map \(a \mapsto eae^{-1}\) defines an automorphism of \(A_0\) — which, it turns out, must be conjugation by some invertible quaternion \(q\): $$ eae^{-1} = qaq^{-1}.$$ But this means \(q^{-1}e\) commutes with all of \(A_0\), so replacing \(e\) by \(qe^{-1}\) we can assume our automorphism is the identity. In other words, now \(e\) commutes with all of \(A_0\), so \(e^2\) does as well. Thus \(e^2 \in \mathbb{H}\) is actually real. Rescaling \(e\) by a real number we can obtain either \(e^2 = 1\) or \(e^2 = -1\). So, we have two options: That's all!

Ten dimensions of superstring theory

Oh yeah — what about the 10 dimensions in superstring theory? Are they really related to the ten-fold way?

It seems weird, but I think the answer is "yes, at least slightly".

Remember, 2 of the dimensions in 10d string theory are those of the string worldsheet, which is a complex manifold. The other 8 are connected to the octonions, which in turn are connected to the 8-fold periodicity of real Clifford algebra:

So the 8+2 split in string theory is at least slightly connected to the 8+2 split in the list of associative real super division algebras.

This may be more of a joke than a deep observation. After all, the 8 dimensions of the octonions are not individual things with distinct identities, as the 8 super division algebras coming from real Clifford algebras are. So there's no one-to-one correspondence going on here, just an equation between numbers.

Still, there are certain observations that it would be absurd to resist mentioning.

© 2020 John Baez
baez@math.removethis.ucr.andthis.edu

home