So now Trump is deciding whether to use 14-tonne "bunker buster" bomb to attack Iran's uranium enrichment facility deep underground in Fordow, 30 kilometers northeast of Qom.
This bomb is called the GBU-57A/B MOP, for Massive Ordnance Penetrator. It's about 80 centimeters in diameter and 6 meters long. It's not the biggest non-nuclear bomb the USA has ever built – that's the 20-tonne T12. But it could wind up being the largest one ever used.
It's so heavy it cannot be carried by any Israeli bombers, only the US-owned B-2A Spirit bombers. It's a GPS-guided weapon designed to destroy "hard and deeply buried targets" like bunkers and tunnel facilities. Some information claims that it can penetrate 18 meters of concrete, and a US air force article stated that the bomb can penetrate 60 meters underground before exploding.
Supposedly this bomb contains 2 tonnes of AFX-757. This is a mix of 30% ammonium perchlorate, 33% aluminum (yes aluminum is highly flammable under the right conditions), 25% RDX and some other stuff.
RDX stands for Research Department Explosive or Royal Demolition Explosive – it's the highly symmetrical compound shown above. It's also called 'hexogen', for the obvious reason. It was developed by the Brits during WW2, it's the key ingredient in Semtex, and it's the most energetic and brisant of the military high explosives.
'Brisance' is the ability to shatter things.
This bomb is also supposed to contain 330 kilograms of PBXN-114. That stuff is 88% HMX, a chemical also called 'octogen' — see part 2 for a picture of that.
I suppose I should add that I hate war. In a happier world these bombs might be used for impressive fireworks, or not built at all.
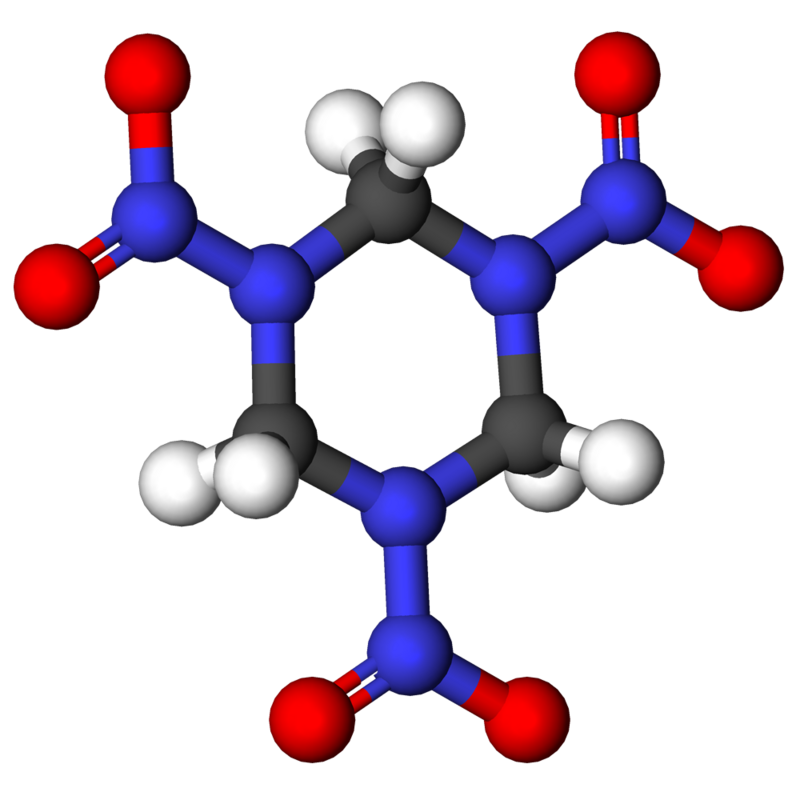
Here is the molecule 'HMX', another explosive used in the GBU-57A/B Massive Ordnance Penetrator. Like the first molecule I showed you, it's a symmetrical ring of carbon atoms (black) alternating with nitrogen atoms (blue), with further nitrogens poking out, and oxygen atoms (red) attached to those, along with some hydrogens (white).
In fact they are almost the same, except RDX has 3-fold symmetry and HMX has 4-fold symmetry.
You'll notice that the 2.3 tonnes of explosives is a lot less than the total mass of the bomb! I guess the rest is mainly the "high-density steel alloy designed to withstand extreme impact forces during penetration".
Wikipedia says:
In 2002, Northrop Grumman and Lockheed Martin were working on the development of a 30,000-pound (13,600 kg) earth-penetrating weapon, but funding and technical difficulties resulted in the development work being abandoned. Following the 2003 invasion of Iraq, analysis of sites that had been attacked with bunker buster bombs revealed poor penetration and inadequate levels of destruction. This renewed interest in the development of a larger bunker buster, and the MOP project was initiated by the Defense Threat Reduction Agency to fulfill a long-standing Air Force requirement.
The MOP bomb was finally tested in 2007. In 2011 the US air force got about 20 MOPs, in 2012, the Pentagon requested $82 million to develop a more powerful version, and a 2013 report stated that the development had been a success.
Now Trump has just demanded "UNCONDITIONAL SURRENDER!" from Iran.