

This is Ambulocetus, the ambling cetacean. That is, the walking whale!
Its fossil remains date back to 48 million years ago. In fact we now think it mainly swam, by paddling. But it's a descendant of Pakicetus, which still walked on land around 50 million years ago.
Modern whales may be be descended from Ambulocetus. Its closest current land-dwelling relative is the hippopotamus.
Fossils of both Ambulocetus and Pakicetus were found in Pakistan — hence the name 'Pakicetus'. Back when they were alive, the Indian subcontinent was an island, just beginning its collision with Asia which would eventually form the Himalayas. There were mangroves on the western shores, and it seems Ambulocetus was an ambush predator that ate large mammals which approached the water's edge, or ancient relatives of manatees.
Ambulocetus was about 4 meters long. Later whales became much bigger, especially those that filter water for small prey. The largest mammals ever are alive today!
For more, see:
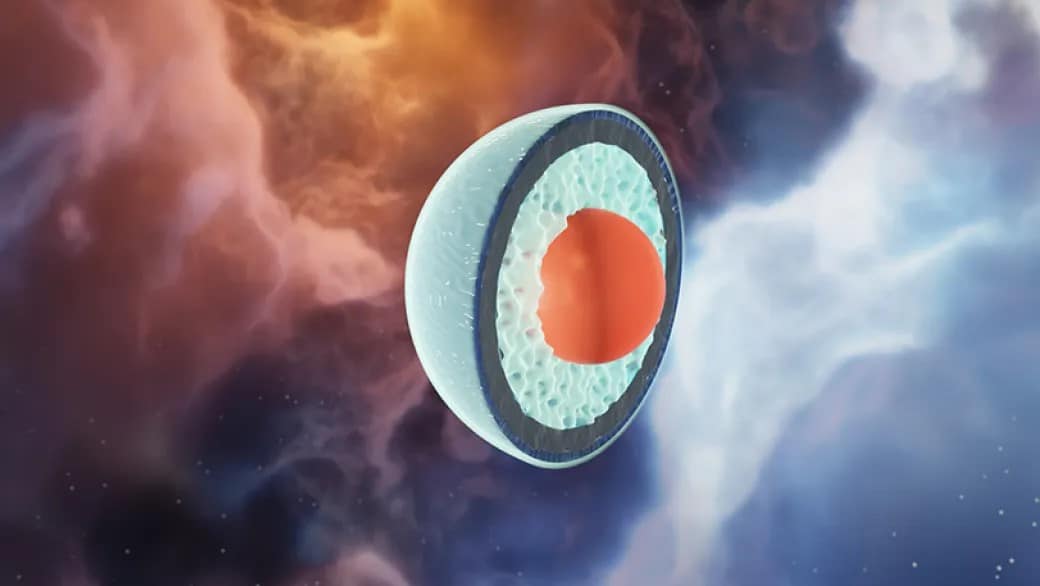
Wow — evidence that very massive neutron stars may have cores made of deconfined quark matter! The idea of a 'quark star' is not new, but I didn't know it was a serious possibility.
An ordinary neutron star has a core made mostly of densely packed neutrons. A matchbox-sized chunk of this stuff weighs about 3 billion tonnes. But if you squeeze this stuff hard enough, eventually the neutrons break. Each neutron consists of 3 quarks held together by gluons. So when the neutrons break you get 'quark matter' — a sea of quarks and gluons, no longer confined in neutrons.
We've made something similar here on Earth: at CERN and Brookhaven, physicists smack atomic nuclei at each other so hard that the protons and neutrons break and momentarily form a 'quark-gluon plasma'. But the conditions in a neutron star core are different: cooler, but more pressure — and not just temporary.
This new paper tries to take the measured properties of massive neutron stars and see if they fit a model where the inner core is made of deconfined quark matter:
For me, the coolest part is that deconfined quark matter may have an extra symmetry, called 'conformal symmetry'. This means that if you zoom in on it, it looks almost the same. An atom looks like a blob with some specific size. So does a neutron. But a system with conformal symmetry is just a blur spread out everywhere — and if you zoom in or zoom out, you see something very similar. This is crazy.
We see matter with conformal symmetry elsewhere too, like at 'critical points'. As you know, when you heat water it boils. There's a sharp divide between liquid and gas. But as you keep boosting the pressure, the boiling point increases. And at 647 degrees kelvin and 220 times ordinary atmospheric pressure something weird happens: the distinction between liquid and gas ends! This is called a 'critical point'.
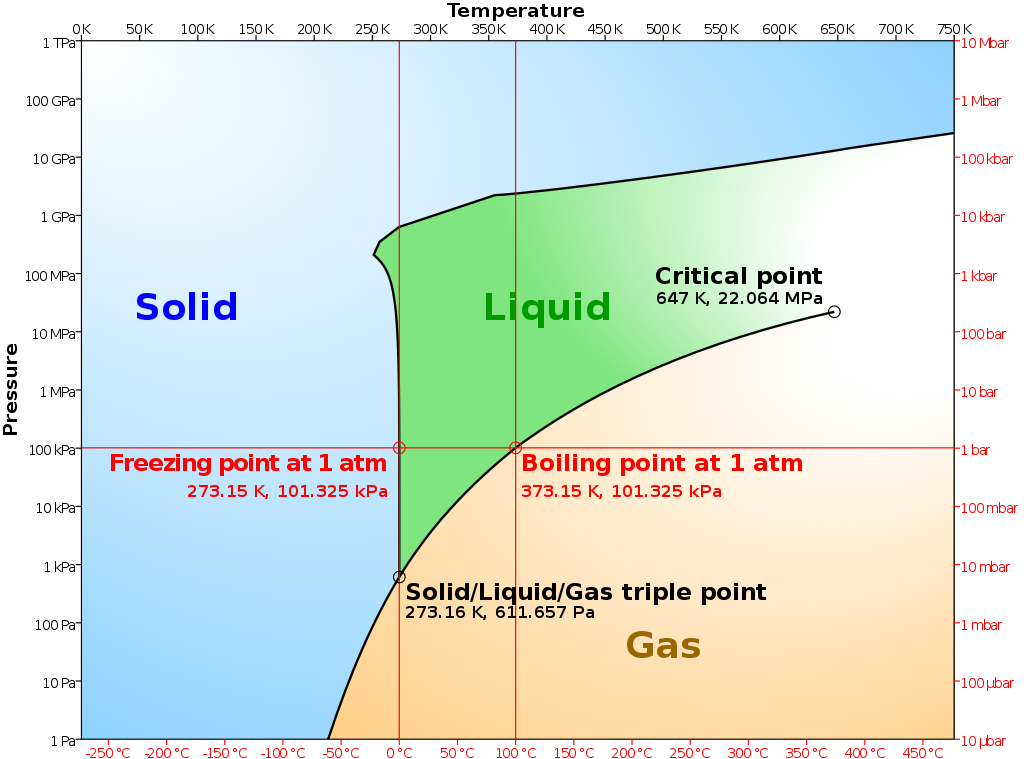
Right at the critical point, water looks weird. It look like a blur of droplets floating in gas. But if you look at any droplet you'll see it's full of bubbles of gas. And if you look in any of these bubbles you see it's full of droplets. As you keep zooming in, you keep seeing basically the same thing.... droplets of liquid in gas, bubbles of gas in liquid.... until you get down to the scale of atoms. So we say this stuff has 'conformal symmetry'.
The math of this is incredibly cool: it's called 'conformal field theory', and a lot of mathematicians and physicists study it. So it would be really neat if extremely heavy neutron stars turn out to be made of deconfined quark matter with conformal symmetry... or even just approximate conformal symmetry.
July 10, 2024

What would happen if you could take a piece of matter from a neutron star and keep heating it up under pressure? You can pump more and more energy into it — but according to Rolf Hagedorn's calculations back in 1964, its temperature will never go above 1.2 trillion kelvin! Past that point, all the energy goes into creating more and more new kinds of particles and antiparticles.
You see, the matter in a neutron stars is not just neutrons. It's also made of protons and other kinds of particles, called hadrons. Only the lightest of these are common at low temperatures. But if you could heat the matter in a neutron star, so the neutrons start colliding with each other more energetically, there would get to be enough energy that more and more different kinds of massive particles get created in these collisions.
At least that was his theory. Now we know that all these particles are made of quarks and gluons, and when the temperature gets high enough these particles smack into each other so hard that they just break, creating a quark-gluon plasma.
But his idea of a maximum temperature was a good one. Whenever the number of energy levels of a system grows exponentially or faster with temperature, it will have a maximum temperature! And this is called the 'Hagedorn temperature'.
The simplest example is the 'primon gas', a theoretical gas where there's one kind of particle for each prime number, and the energy of the prime \(p\) is \(\ln p\). The partition function of this gas is the Riemann zeta function. As you heat this gas, you approach the pole at \(z = 1\), and you create a shitload of prime numbers.... in theory.
I'm writing about this in my book on entropy:
Cool news about Omega Centauri!
First, what is Omega Centauri? It's the largest of roughly 200 globular clusters that roam the outskirts of our galaxy. It packs 10 million stars much older than the Sun into a ball 150 light-years in diameter. We think it was a small galaxy in its own right that got captured by ours and stripped of its outer layers.
The news is that Omega Centauri seems to have a black hole in its center, just like many galaxies. But this black hole is just 8,000 times the mass of our Sun!
Yes, that's huge compared to a black hole formed by a single collapsing star... but it's tiny compared to the typical 'supermassive' black holes found at galactic centers. It's the first 'intermediate mass' black hole ever found! Astronomers have been looking for them.
This black hole may be a rare remnant — a fly in amber. Maybe all black holes in galactic centers started small and kept growing by eating stars until they became supermassive. Maybe Omega Centauri stayed small because its host galaxy got ripped apart by ours.
Why do we think Omega Centauri has a black hole in it? A team led by Maximilian Häberle at the Max Planck Institute for Astronomy found seven stars in its core moving so fast that they would have shot out of the cluster if there weren't a massive object holding them in.
Häberle has been working at this since 2019, measuring the velocities of 1.4 million stars in Omega Centauri by studying over 500 Hubble images of the cluster. Most of these images had been produced for another purpose: calibrating Hubble’s instruments. But they turned out to be perfect for the job of finding fast-moving stars.
More details:
Did you ever wonder why there are 90 degrees in a right angle instead of 100, and 24 hours a day instead of 10?
Perhaps you can blame Napoleon.
In 1795, as part of the French Revolution, the French passed a law requiring that clocks have 10 hours in a day, 100 minutes in an hour, and 100 seconds per minute. They also brought in a system of angles with 400 degrees in a full turn, or 100 degrees in a right angle. With this, the earth would rotate 40 degrees in an hour — and thanks to how the meter was defined, each degree of latitude would be 100 kilometers long.
Of course, changing to the new system would require a lot of work. The economist Condorcet proposed that teams of unemployed wig makers be used to calculate mathematical tables with the new units. Why wig makers? Because after the revolution, aristocrats no longer needed them! (You don't need a wig if you don't have a head.)
The mathematical physicist Laplace was enthusiastic and had his watch converted to the new time. His great five-volume work Traité de Mécanique Céleste was written using the new units of time and angle! But in general the metric system for time and angle did not catch on, despite the law. And in 1806, Napoleon Bonaparte decreed that the French calendar should revert to the old style.
More details are here:
Ever think about how weird it is that purple, a mix of red and blue, looks like violet? Red and violet are at the opposite ends of the visible spectrum!
This diagram of colors sheds some light on this. Its boundary consists of two parts: a curve and a straight line.
Your computer screen probably uses a red-green-blue system, so it can only make colors inside the triangle here, or some nearby triangle. The colors in the triangle are called the gamut.
In the gamut, colors close to the purple line are made as mixtures of red and blue.
There's a huge amount more to say about this, and I don't know most of it yet. The above diagram is called the 'CIE xy chromaticity diagram', and it's explained here:
What color is the river Styx — the river that the dead must cross to reach the underworld in Greek myths?
'Stygian blue' would be a good name for it. But Stygian blue is actually what you see by staring at this yellow dot for a long time and then looking at the black square. It's a weird color: somehow simultaneously deep blue and black.
Stygian blue is an example of a 'chimerical color'. This means it can only be seen by looking steadily at a strong color until some of your cone cells become fatigued, temporarily changing their behavior. If you then look at a new color, an afterimage with the color opposite to the one you were staring at gets overlaid on the new color.
Chimerical colors are fun because they can't be explained by the usual simple theory of vision! In the simple theory, each of the 3 kinds of cone cell is getting activated by some amount, so you just need 3 nonnegative numbers to describe a color. To explain chimerical colors, people resort to more complex theories of vision, like these:
How does it work? The complementary color of orange is blue-green, or more precisely 'cyan'. Staring at a cyan dot for a long time tires out your cone cells: it wears out their response to cyan light. When you look at something white, you then see an orange afterimage. But if you look at something orange, you see an orange color stronger than ordinarily possible.
Like Stygian blue, which I showed you yesterday, hyperbolic orange is a 'chimerical color': a color that's not possible in the usual simplified theory of color vision, which only becomes possible when some of your cones are fatigued. These were discussed here:
The fifth note of the major scale is called the dominant. In the key of C it's G.
A dominant seventh chord is a 4-note chord where you start at the dominant and go up the major scale skipping every other note. In the key of C it's the notes in boldface here:
Below I've drawn blue edges from G to B, from B to D, and from D to F:

Any dominant seventh chord has two notes that are opposite each other — shown in orange here. We say they're a tritone apart.
A tritone is very dissonant, so the dominant seventh chord really wants to 'resolve' to something more sweet. This tendency is a major driving force in classical music and jazz! There's a lot more to say about it.
But never mind. What if we take my picture and rotate it 180 degrees? Then we get a new chord! This trick is called a tritone substitution.
Let's look at it:
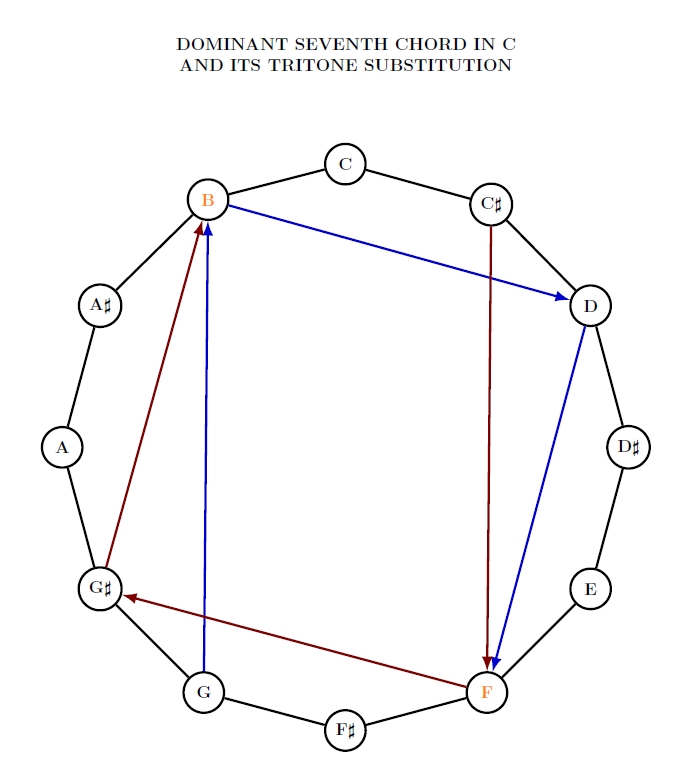
Here you see our original dominant seventh chord (with notes connected by blue edges):
Each note in the tritone substitution is a tritone higher than the corresponding note in the dominant seventh chord — so it's the point on the opposite side of the circle.
But two notes in the dominant seventh were directly opposite each other to begin with: B and F. So these two notes are also in the tritone substitution!
This makes the tritone substitution sound a lot like the original dominant seventh chord.
See the square of notes? Three are in the original dominant seventh, and three are in the tritone substitution. Musicians like such squares of notes, even though they're quite dissonant. They're called diminished seventh chords. But let me stop here instead of blasting you with too much information.
Let's actually listen to some tritone substitutions:
Here David Bennett plays a bunch of songs that use tritone substitutions. I'm very glad to learn that the slippery, suave sound at a certain point of The Girl from Ipanema comes from using a tritone substitution. He also plays a version without the tritone substitution, and you can hear how boring it is by comparison!
Music theorists tend to bombard their audience with more information than nonexperts can swallow in one sitting. David Bennett could have made a nice easy video full of examples where musicians apply a tritone substitution to a dominant seventh chord in its most natural position, where it starts at the 5th note in the major scale. But you can also take a dominant seventh chord and move it up or down, getting a chord called a secondary dominant, and then do a tritone substitution to that. And Bennett feels compelled to show us all the possibilities, and how they get used in fairly well-known tunes.
If you start getting overwhelmed, don't feel bad. Let me show you another explanation of tritone substitutions:
I really love the friendly, laid-back yet analytical style of Michael Keithson. He's great at explaining how you could have invented harmony theory on your own starting from a few basic principles. He's like the music theory teacher I always wish I had.
His pose above is a parody of the sneaky suave punch that a tritone substitution can pack. Speaking of which, if you want to sound like a hipster, you say tritone sub. Don't mix this up with the submarine used by the Greek sea god born of Poseidon and Aphrodite: that's the 'Triton sub'.
In this video Keithson explains tritone subs. He starts out basic. Then he gets into all the ways you can use a tritone sub. You may want to quit at some point when it gets too complicated. I think it's better to just zone out and listen to his piano playing. Even if you don't follow all his words, you'll get a sense of what tritone subs can do!
Understanding tritone subs well requires understanding dominant chords, and Keithson has a good lesson on those, too: