The periodic table is a delightful mix of patterns and exceptions. To figure it out, you just need to know how electrons orbiting a nucleus arrange themselves to minimize energy. But that's a tough math problem: you need a computer to solve it from first principles.
Luckily you can get quite far with a massive simplifying assumption: the electrons don't interact with other. Then you can figure everything out using 'group representation theory', an elegant branch of math that let you use symmetry to crunch quantum problems. This predicts that electrons come in 'subshells' which form larger 'shells'. And it predicts exactly how these subshells and shells work.
The electrons do interact with each other! But you can use a few rules of thumb to guess how this changes the story. They're not perfect, but they're damned good. Nobody really knows.
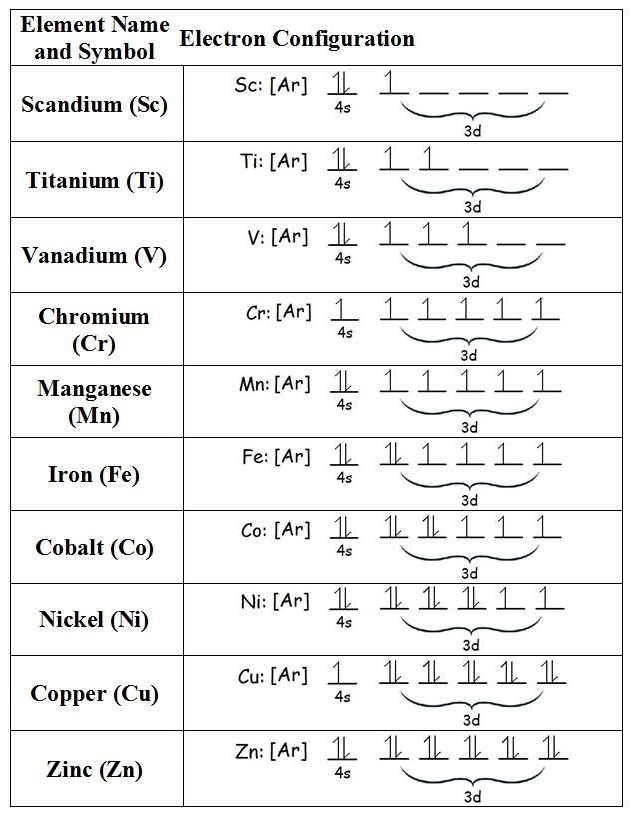
For example, check out the first row of 'transition metals' in the periodic table.
They have all the electrons that argon does — that's the [Ar] in the chart. Most have two electrons in the 4s subshell: one spin up, and one spin down. So the action mainly happens in the 3d subshell. This has 10 slots for electrons, so we get 10 different metals. This subshell stuff comes from group representation theory. Tons of fun.
The 'Hund rules' say first we get 5 metals with 1, 2, 3, 4, and 5 spin-up electrons, and then 5 more metals that add in 1, 2, 3, 4, and 5 spin-down electrons. And that's almost what we see.
But notice: when we hit chromium we get an exception! Chromium steals an electron from the 4s subshell to get 5 spin-up electrons in the 4d subshell. We get an another exception when we hit copper. Can you guess why?
The short answer is that electrons in the d subshell can lower their energy if the maximum number possible, namely 5, have their spins pointing in the same direction. (I've been arbitrarily calling direction 'up', but there's nothing special about the 'up' direction so don't lose sleep over that.)
We naturally get 5 spin-up electrons when we hit manganese, with 5 electrons in the d subshell. But the energy-lowering effect is strong enough that chromium 'jumps the gun' and steals one electron from the somewhat lower-energy s subshell to put 5 spin-up electrons in its d subshell!
Copper jumps the gun in a similar way, getting 5 spin-up and 5 spin-down electrons in the d subshell by stealing one from the s subshell.
The completed d subshell makes copper soft compared to, say, its neighbor nickel. And the lone electron in its 4s subshell makes copper a great conductor of electricity: this electron can easily hop from atom to atom. In fact, blue and green light are energetic enough to push those electrons around, so copper absorbs blue and green light… while still reflecting the lower-energy red light!
Similar things happen with the elements directly below copper in the periodic table: silver and gold. But it would take more work to understand why copper, silver and gold have different colors.
To learn a bit more about how we use group representation theory to understand
the periodic table and the behavior of the d subshell, go to my November 30 and December 8, 2021 diary entries.
June 8, 2024
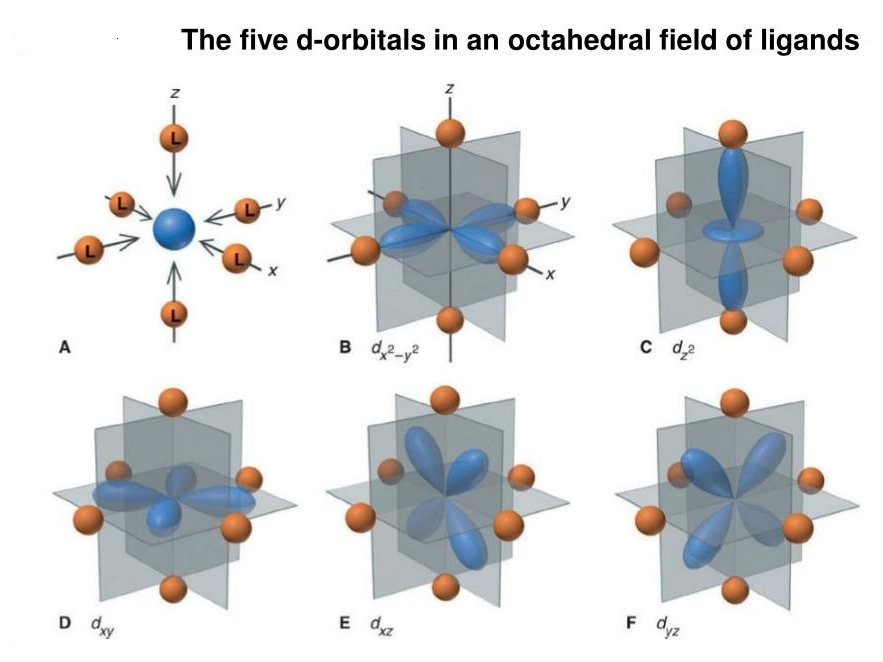
I'm having fun learning about 'crystal field theory'. It sounds so cool! It's actually a specialized subject where we look at a transition metal atom surrounded by nearby molecules called 'ligands'. Here you see 6 ligands at the vertices of an octahedron. Each repels the electrons of your transition metal atom in the middle.
A transition metal atom has up to 10 electrons in its 'd orbitals'. These are shown as blue blobs here. There are five d orbitals, and each can hold at most 2 electrons: one 'spin up' and one 'spin down'. That gives a total of 10.
Before you surround the atom with ligands, electrons in all five d orbitals have the same energy. But because the ligands repel these electrons, the energies of the d orbitals called B and C get pushed up compared to those called D, E, F - because B and C's blue blobs get closer to the ligands!
Now for the math. A 'd orbital' corresponds to a homogeneous quadratic polynomial in the 𝑥,𝑦,𝑧 coordinates that has Laplacian equal to zero. Every d orbital is a linear combination of these five:
B: \(x^2 - y^2\)
C: \(2z^2 - x^2 - y^2\)
D: \(xy\)
E: \(xz\)
F: \(yz\)
Note the Laplacian of each function is zero! Also note that \(z^2\) in the picture is short for \(2z^2 - x^2 - y^2\).
It's purely arbitrary that the two weirdo orbitals, B and C, treat the \(z\) axis differently than the \(x\) and \(y\) axis. We could choose other d orbitals that treat the \(x\) or \(y\) axes differently.
If you rotate a d orbital you get another d orbital, so we say d orbitals form a 'representation' of the rotation group. But the ligands break the rotational symmetry! With the ligands around, the symmetry group is reduced to the symmetry group of an octahedron.
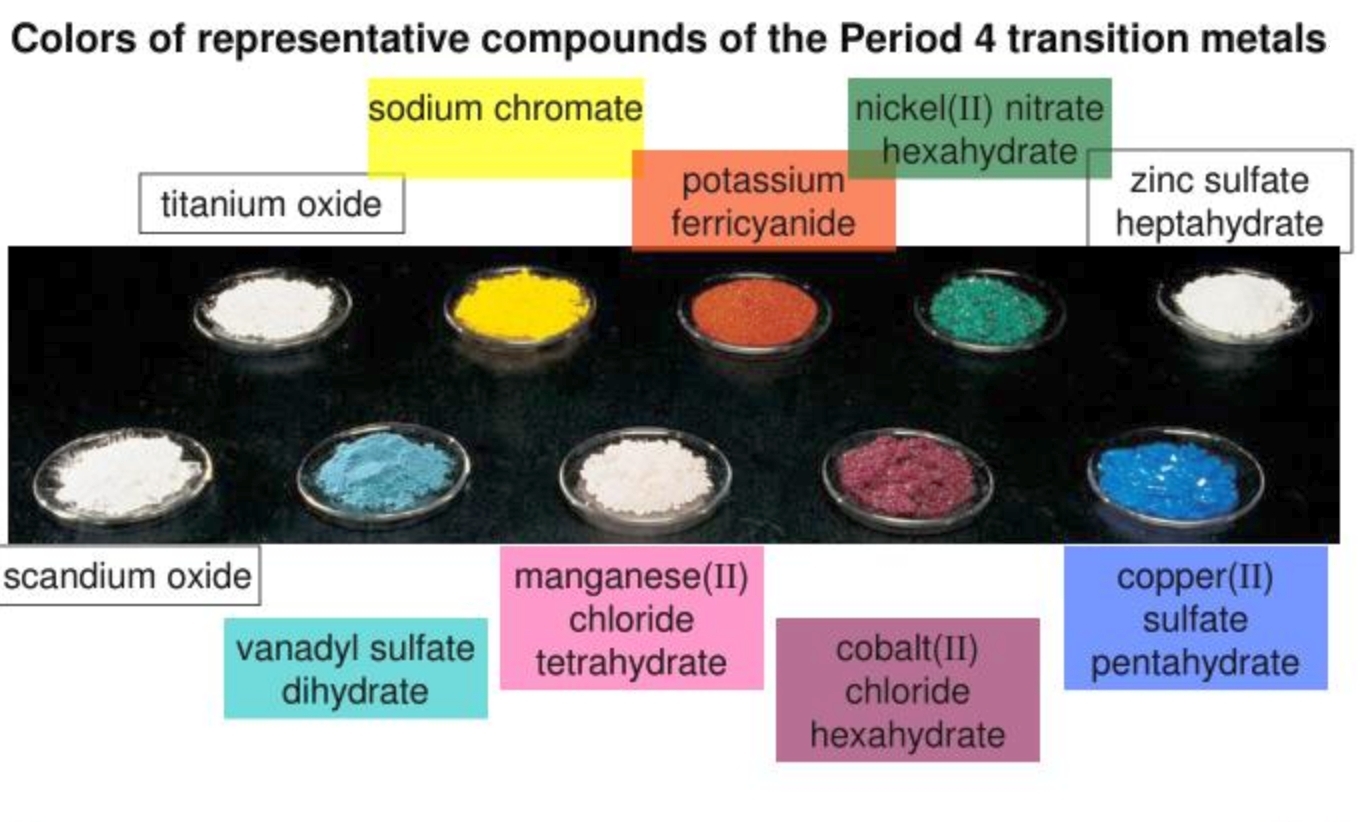
What's the point of this math? It's used to explain the colors of transition metal compounds. Yes, the symmetries of polynomials are important for understanding the colorful world of pigments!
More of the math:
Rotation and reflection symmetries of an octahedron permute the \(x, y,\) and \(z\) coordinates and also introduce minus signs. These transformations send the d orbitals
D: \(xy\)
E: \(xz\)
F: \(yz\)
to themselves, or minus themselves, so these d orbitals are basis vectors for a 3d representation of the octahedral symmetry group.
Less obviously, these transformations send the d orbitals
B: \(x^2 - y^2\)
C: \(2z^2 - x^2 - y^2\)
to linear combinations of themselves, so these d orbitals are basis vectors for a 2d representation of the octahedral group!
Why is that last bit true? Say we do a 90 degree rotation in the \(xz\) plane. Then \(x^2 - y^2\) becomes \(z^2 - y^2\), but this is still a linear combination of functions B and C, since
B + C = \((x^2 - y^2) + (2z^2 - x^2 - y^2) = 2z^2 - 2y^2\)
Similarly \(2z^2 - x^2 - y^2\) becomes \(2x^2 - z^2 - y^2\), which, you can check, is -B/2 + 3C/2. So even though the weirdo orbitals B and C aren't preserved by octahedral symmetries, linear combinations of them are!
You can learn the chemistry here:
and that's where I got the pictures!
June 10, 2024

I just noticed that my new flat has two things that look like windows from outside, but are invisible from inside! This raises lots of questions.
They're the two with 12 panes each, on the top floor. The windows directly below are also gone: once upon a time Edinburgh imposed a tax on windows, and people blocked them off to save money. But I've never seen it done the way it is in my flat, with the windows left intact outside. One of them is behind a 'press', a shallow closet typical of these parts. Another is lurking behind the wall in my office somewhere! I wish I could get at it. Maybe there's a skeleton in there.
Here are some more typical blocked-off windows in Edinburgh:

For a long time people thought noble gases were too snobbish to form compounds, but in 1962 Neil Bartlett produced xenon hexafluoride.
Most xenon compounds involve fluorine, chlorine and oxygen — elements so aggressive they ignore the standoffishness of this noble gas, slap it right on the back and say "hey, pal! I'm moving in!" But as a result, some of these compounds are dangerous. Xenon trioxide and xenon tetroxide are explosive. Xenon oxytetrafluoride, shown above, is extremely reactive, and it forms hazardous and corrosive byproducts when mixed with water.
A much more mellow chemical is tetraxenonogold — the first discovered compound involving a noble gas and a noble metal! But to make it, you use fluorine.
As far as I can tell, all these xenon compounds are created by chemists just to provide interesting Wikipedia articles for me to read while sipping coffee in bed:
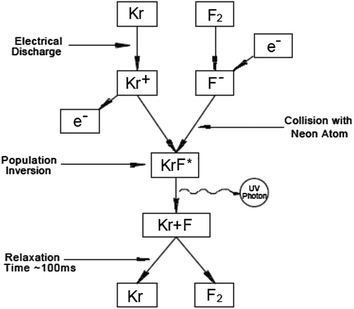
Yesterday I made it sound like chemists create weird molecules like noble gas fluorides just for fun. That may be true to some extent. But something even more far-out, KRYPTON FLUORIDE ULTRAVIOLET LASERS, have been important in a multi-billion-dollar industry — namely, carving semiconductor chips!
To me the cool part is the underlying physics. A single krypton and a single fluorine atom don't stick together to form a molecule. KrF2 is a thing, but not KrF. However, if you 'excite' the krypton and fluorine atoms, knocking them up into a higher energy state, they do stick together and form something called KrF*... until they release some ultraviolet light and lose that extra energy. Then they fall apart!
You can use this to make a powerful ultraviolet laser beam. And since ultraviolet light has a short wavelength, you can use this to carve chips at a finer resolution than you could with visible light.
KrF* is called an 'excimer'. An 'excimer' is a pair of atoms that only stick together to form a kind of molecule-like thing when they're in an excited state. Excimers don't last long — just nanoseconds. It seems almost paradoxical that something could hang together better when it has more energy, but that's the fun of excimers.
By now there are various kinds of excimer laser. Some use krypton fluoride, but Lasik eye surgery uses argon fluoride.
Read all about it:
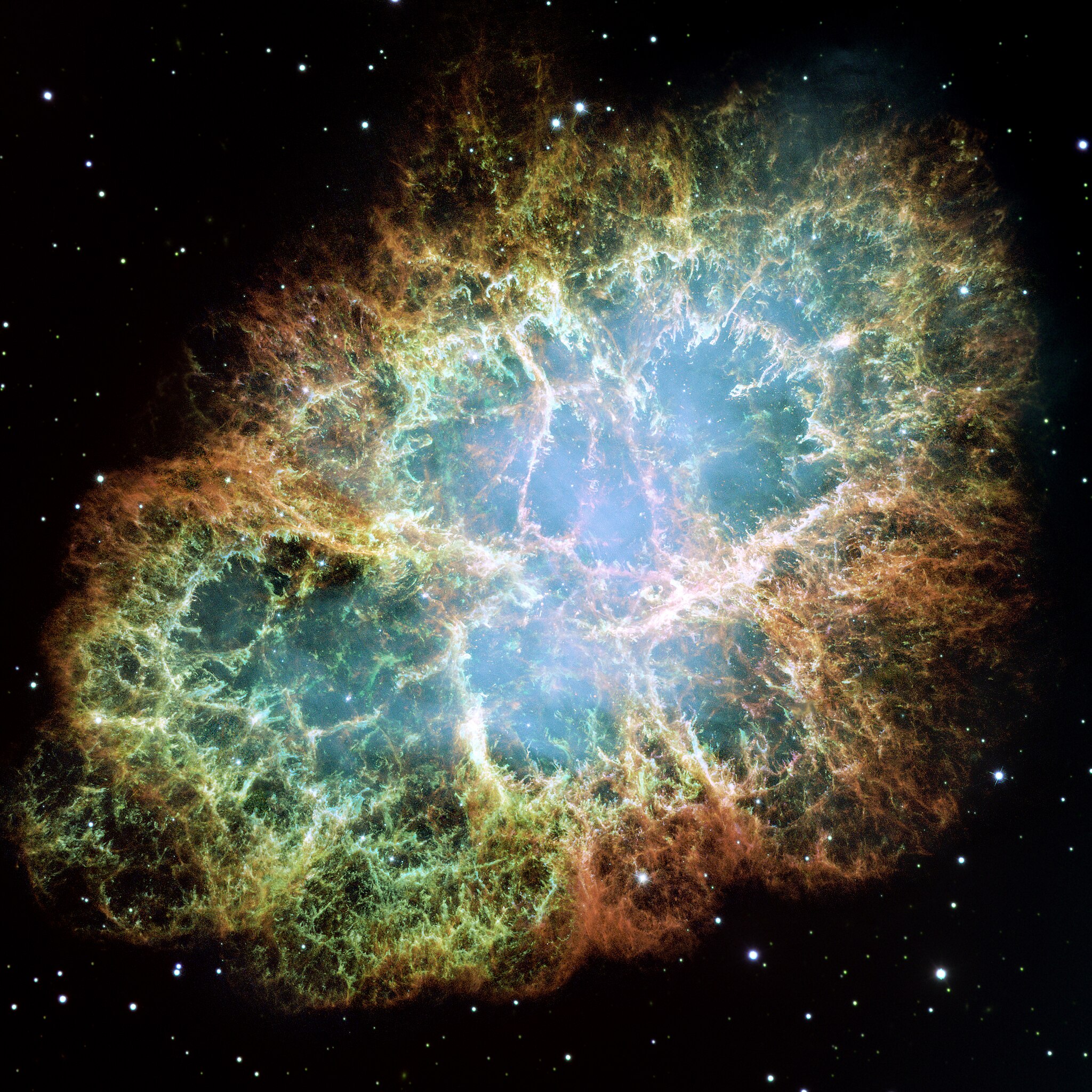
Argonium. Is that really a thing? Yes! And we've found it in a supernova remnant.
It's not simply argon hydride, ArH. That's just barely a thing. After all, a noble gas atom and a hydrogen atom repel each other at normal intermolecular distances.
You can make a molecule of ArH if you put the hydrogen quite far from the argon atom: then a weak attraction called the van der Waals force will attract them. This is called a 'van de Waals molecule'. But it's a very delicate thing.
Another thing you can do is make ArH with one electron in a high energy state. This is called an 'excimer' and written ArH*. It lasts until the electron emits light and falls to a lower energy state. Then your molecule breaks apart because the hydrogen is close to the argon and they repel.
A limiting case of an excimer is to make ArH with one electron simply missing. Then you've got the ion ArH⁺. This is quite stable. And it goes by the romantic name 'argonium'.
People have found lots of argonium in the Crab Nebula, which is a remnant of a supernova. We can see it by the special frequencies of light it emits. It seems to be formed when argon atoms ionized by cosmic rays meet hydrogen molecules:
When it's formed it's in an excited state; then it settles down, emitting light.
It's pretty cool that noble gases, supposedly so resistant to combining with anything, do it easily enough that we can see it happening in this violent environment!
Wikipedia has a surprisingly long article on this:
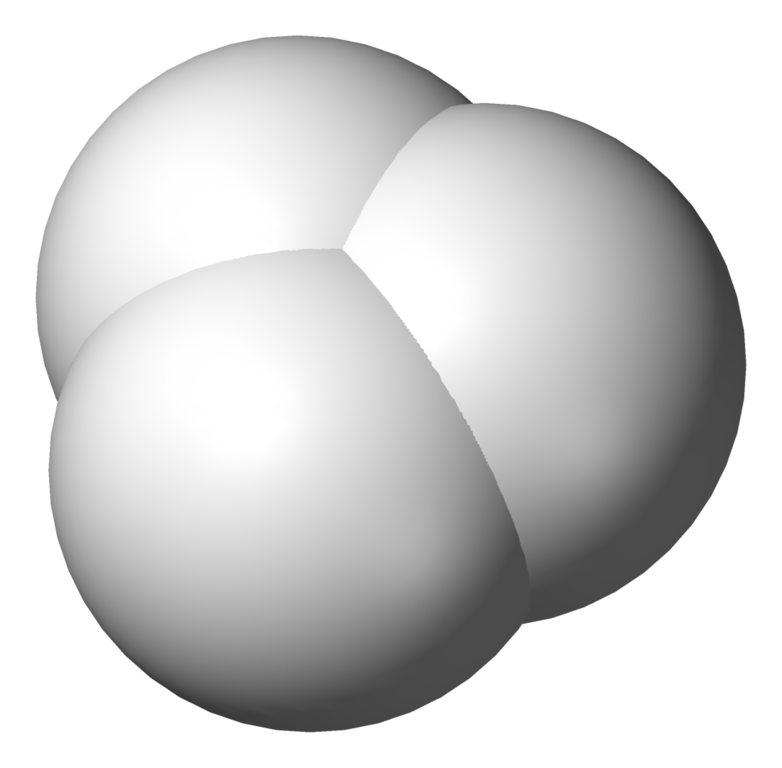
Did you know one of the most common ions in interstellar space is hydrogenonium?
Now we're just getting silly — right? 'Hydrogenonium'? It sounds like something my seven-year old cousin would make up. But it's real! Or at least it's the official name, proposed by the International Union of Pure and Applied Chemistry, for three hydrogen atoms stuck together, missing one electron: H3+.
Normal chemists call this the 'trihydrogen cation'. It's the simplest thing made out of 3 atoms. Out in space, it gets formed like this. First a high-energy proton called a 'cosmic ray' can knock an electron off a hydrogen molecule:
and move right on by. Then the H2+ can bump into another hydrogen molecule and form a trihydrogen cation:
There are also various mechanisms for H3+ to get destroyed. It can bump into another molecule, and in very empty space it eventually falls apart, since this increases entropy by an arbitrarily large amount. (In fact this happens to any molecule: a little-known and scary fact that will make the far future quite boring.) But H3+ counts as 'stable' because it takes energy to rip it apart.
Like argonium, ArH+, the trihydrogen cation is stable even though the corresponding molecule is not. J. J. Thomson, the guy who discovered the electron, believed that H3 should be stable. So did Niels Bohr! But Thomson was only able to make H3+. He never found H3. Indeed, that lasts for less than a microsecond.
For the comic history of ideas on H3 and H3+, see this:
But the two helium atoms aren't held together by a bond. Instead, they're held together by a much weaker force: the van der Waals force. So this isn't an ordinary molecule. It's huge! The distance between nuclei is 70 times bigger than it is for H2. And it's very loosely held together, so you'll only see it at extremely low temperatures.
Such a molecule held together by the van der Waals force is called a van der Waals molecule.
But what's the van der Waals force? This is actually a name for a few different forces that exist between electrically neutral objects:
For dihelium, the most important force is the London force, which unfortunately is the hardest one to understand. But qualitatively it works like this:
Start with two neutral atoms. Each is a nucleus surrounded by electrons. If they start out spherically symmetric, like helium, and far enough apart that their electron clouds don't overlap, there should be no electrostatic force between them.
But wait — the electrons are randomly moving around! Sometimes they move to make each atom into a 'dipole', with the nucleus on one side and the electrons over on the other side. If these two dipoles point the same way, this lowers the energy — so this will tend to happen. And now the two atoms attract... since two dipoles pointing the same way attract.
But this effect is small. The gif vastly exaggerates how much the electrons move to one side of each proton. And this van der Waals force dies off fast with distance, like \(1/r^7\). So we have two objects held together by a very weak force. That's why the helium dimer is so huge.
Now let's think a bit about why the van der Waals force obeys a \(1/r^7\) force law. Where the heck does that number 7 come from? It's so weird! It's best to warm up by considering some simpler force laws.
We can use this idea to explain what's going on with two helium atoms — but only in very hand-wavy way, where we imagine superpositions are like probability distributions. A better explanation must use quantum mechanics.
This is called the London force. It's morally similar to the Keesom force because we look at the combined system in its ground state, or lowest-energy state, and this happens when the electrons of each atom move in such a way to create two aligned dipoles... a lot like in the gif above.
But while the derivation in the paper is widely used, it's pretty sketchy, since it approximates the electrons with harmonic oscillators, as if they were attached to their locations with springs! This is called the Drude model.
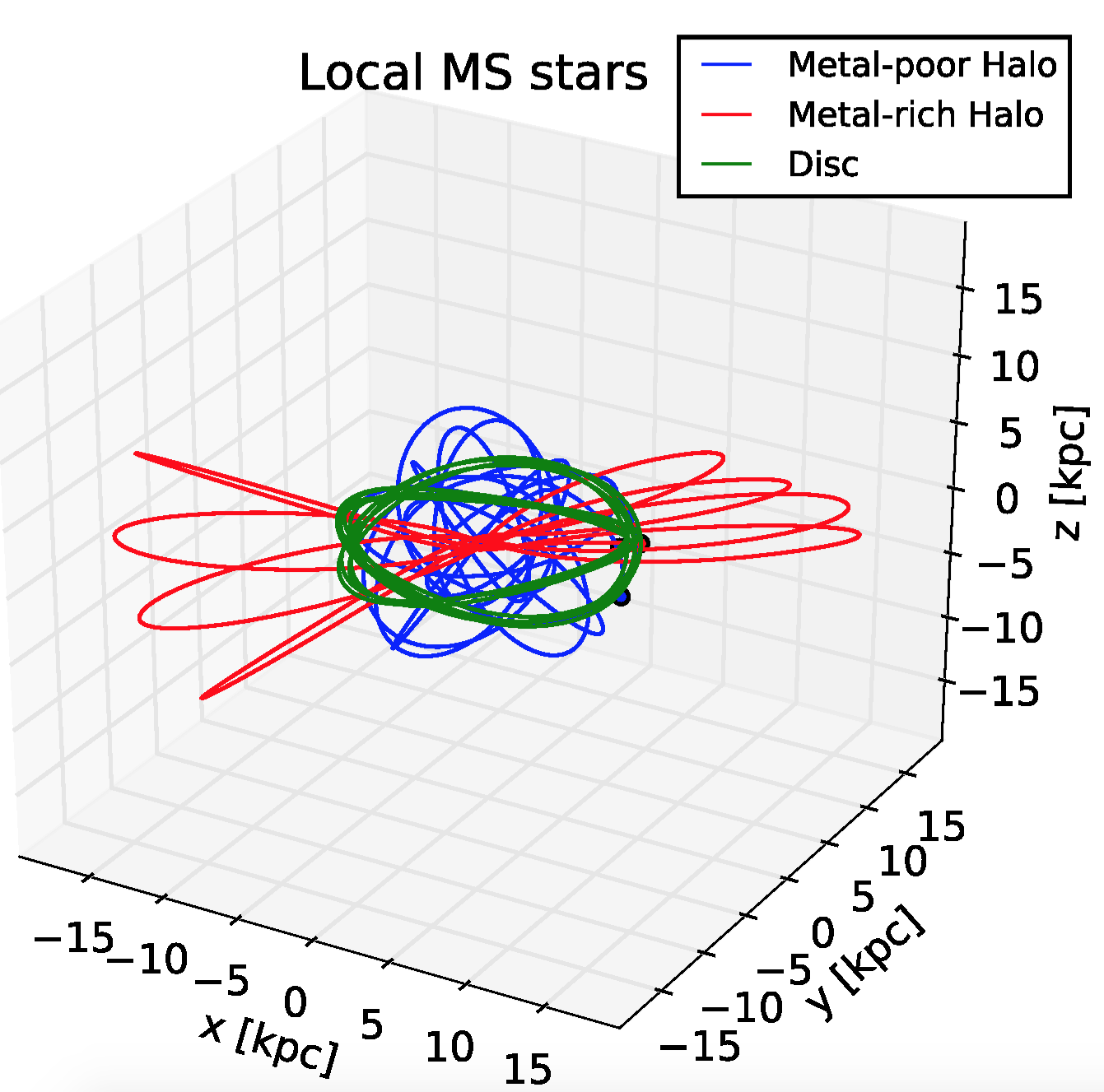
The last time a big galaxy crashed into ours was between 8 and 11 billion years ago. It added about 50 billion solar masses to our galaxy. And its remains, still visible today, are called the Sausage.
Why the funny name? It's the red thing in the picture! This picture shows orbits of various typical stars in the Milky Way. The z direction is at right angles to the galactic disk. There are 3 quite different kinds of stars:
You see, redshifts are only good for telling if something is moving toward or away from you. Stars in the Sausage are moving back and forth from our point of view. Gaia accurately measured the position of a billion astronomical objects, measuring each 70 times in its five-year life! So it could actually see a bunch of stars slowly moving across the sky.
For more on the Sausage:
For 6 weeks our team met in Maxwell's childhood home in Edinburgh, working on software for agent-based models.
We developed a category-theoretic framework that lets you model discrete structures that change randomly at discrete moments in time, coupled to continuous variables that evolve according to ordinary differential equations. It's incredibly flexible! We've written code for a lot of it, but there's more to do. And I need to write explanations — illustrating the math and software with a bunch of well-known COVID models. So we'll keep meeting on Zoom.
But still, I have more free time now! I want to finish a bunch of papers.... and books. It's a bit intimidating, but one at a time:
A volunteer search and rescue recently found this object in the Desert National Wildlife Refuge about 16 miles north of Las Vegas. Nobody knows how it got there.
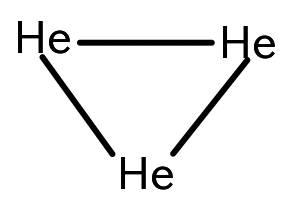
On June 15th I talked about dihelium. This consists of 2 helium atoms held together, not by a chemical bond, but by the weak left-over remnants of the electrical forces holding each atom together. Trihelium works the same way, but it's more stable than dihelium. Indeed if you took one of the larger forms of trihelium and removed any one of the 3 atoms, the other two would fly apart.
This bizarre phenomenon was predicted by the Russian physicist Vitaly N. Efimov in the 1970s. He showed it should happen whenever you have 3 identical bosons attracting each other by a short-range force. As they come closer and closer to having enough energy to no longer be bound together, they form an infinite sequence of bound states, where the radius of the nth state is proportional to the \(n\)th power of some number \(\lambda\). This number \(\lambda\) is close to 22.6948, but Efimov showed that it's actually
$$ \exp(\pi/s) $$
where \(s\) is the unique positive solution of
$$ s \cosh(\pi s/2) = 8 \sinh(\pi s/6)/\sqrt{3} $$
Alas, I don't understand his calculation.
For a long time Efimov's work was just a theoretical prediction. In 2014 a team observed the first two 'Efimov states' in an ultracold gas of cesium. But trihelium is harder to work with, and it's only with great trouble that people have made it at all. So we have not verified that it has Efimov states... but the math and physics is solid.
The journal Physics has a nice article on Efimov states:
Here's an article on the experimental discovery of Efimov states in cesium:
Why do we call electrons 'negative' and protons 'positive'? It's an arbitrary convention but it's annoying: it means that when electrons flow through wires, the current is defined to flow in the other direction.
If you ask people why electrons got called 'negative', you get a bunch of crap answers:
Yes, but why that convention?
Yeah, it's a convention — but why that convention?
Irrelevant crap which never leads up to an answer.
The answer is that Benjamin Franklin chose this convention and nobody knows why.
In Franklin's day there was a 'two-fluid' theory of electricity saying electricity comes in two kinds. Around 1750 he developed a 'one-fluid' theory after showing that a rubbed glass receives an equal but opposite charge as the cloth used to rub the glass. He decided that electrical fluid was going into the glass. So he said the charge of the glass was 'positive' and the cloth was 'negative'.
Unfortunately it turns out that that electrons are going into the cloth.
The whole history is interesting:
After 3 years I should be able to get indefinite leave to remain in the UK, and Lisa as my spouse can get it in 5 years, so when the job ends we'll be able to spend a lot of time in the UK (but at least 180 days every two years). At least that's the hope.
We're both very excited about this.
What's the problem here? Why did the Big Bang produce so little of heavier elements?
One problem is that the steps after helium are tough. Lithium, beryllium and boron are not very easy to make, for reasons of nuclear physics, so the next one after that — carbon! — first got made by an awkward process where two heliums crash into each other and make an unstable form of beryllium, which decays quickly unless a third helium hits it first, making carbon. This is called the 'triple alpha process':
Once there's a bunch of carbon around, other processes for creating still heavier nuclei come into play. But that happened much later.
Another problem is the 'deuterium bottleneck'.
When a proton and neutron crash into each other, they can stick together and make a deuterium nucleus. After another proton and neutron hit this, you get helium. That's how helium was made in the early Universe. But there was a bottleneck that limited this process!
About 15 seconds after the Big Bang, it cooled down to about 4 billion kelvin: cool enough for all the positron-electron pairs to annhilate. Then all we had was protons, neutrons, electrons and a shitload of light.
But neutrons are more massive than protons, so they become less common as this hot mix cools, with the ratio of their densities being roughly
$$ e^{(m_n - m_p)c^2/kT} $$
at temperature \(T\), as long as reactions are happening fast enough. So it was a race against time to make deuterium by smacking protons and neutrons together. And it was still way too hot for deuterium nuclei to be stable: all that energetic light destroyed them almost as fast as they got
made!
Only later, 3 minutes and 45 seconds after the Big Bang, did it cool down to the point where deuterium nuclei become stable: roughly 1 billion kelvin. Alas, by then most of the neutrons had decayed. There were about 7 protons for every neutron.
At this point, most of the remaining neutrons quickly combined with protons and made deuterium and then helium. But a lot of protons were left without dance partners! So the universe was roughly 3/4 hydrogen and 1/4 helium.
By then, it had cooled down too much for heavier elements to be formed. This only happened much later, in stars. And the universe is still roughly 3/4 hydrogen and 1/4 helium... with a tiny bit of other stuff.
So, the 'deuterium bottleneck' is the fact that deuterium nuclei only hang together at temperatures below 1 billion degrees Celsius, which means they could only start forming 3 minutes and 45 seconds after the Big Bang — almost too late, because most of the neutrons had already decayed.
and for a surprisingly large amount of information on the trihydrogen cation, read
June 15, 2024
Even though helium is the least reactive of the noble gases, you can make a molecule of two helium atoms! Yes, He2 is a thing! It's called 'dihelium' or the helium dimer.
Two point charges: \(1/r^2\)
We start with a single point charge at rest. If you put another point
charge a distance \(r\) away, it will feel a force proportional to
\(1/r^2\). So we say the first charge creates an electric field that
goes like \(1/r^2\).
A point charge and a dipole: \(1/r^3\)
If we put a positive and negative charge in the field of another point charge, but quite close to each other, that other point charge will push on them with a total force proportional to
$$ 1/r^2 − 1/(r + \epsilon)^2. $$
For small \(\epsilon\) this is approximately proportional to the derivative of \(1/r^2\), which is some number times \(1/r^3\). So, we say a dipole in the field of a point charge feels a \(1/r^3\) force.
A dipole and a point charge: \(1/r^3\)
For the same reason, a dipole creates an electric field that goes like \(1/r^3\): if you put a point charge near the dipole, not too close, the two poles in the dipole are at distance \(r\) and \(r+\epsilon\) from this charge, so it feels a force proportional to
$$ 1/r^2 − 1/(r+\epsilon)^2 $$
and we repeat the same calculation as before. Or, just use "for every force there is an equal opposite force".
A dipole and a dipole: \(1/r^4\)
Next consider a dipole in the field produced by another dipole! The first dipole consists of two opposite charges, each feeling the field produced by the other dipole, so the total force on it is proportional to
$$ 1/r^3 − 1/(r+\epsilon)^3 $$
which for small \(\epsilon\) is proportional to \(1/r^4\). So the force between two dipoles goes like \(1/r^4\).
A dipole and an induced dipole: \(1/r^7\)
Next think about a helium atom at a distance \(r\) from a dipole like a water molecule. On its own helium is not a dipole, but in an electric field it becomes a dipole with strength or 'moment' proportional to the electric field it's in, which goes like \(1/r^3\). We know the force between dipoles goes like \(1/r^4\), but now on top of that our helium atom is a dipole with moment proportional to \(1/r^3\), so the force is proportional to
$$ 1/r^4 \times 1/r^3 = 1/r^7. $$
The same calculation works for any initially spherically symmetric neutral object in the field of a dipole, as long as that object is considerably smaller than its distance to the dipole. The object will become a dipole thanks to the field of the other dipole, so we call it an 'induced dipole'. The \(1/r^7\) force between a dipole and an induced dipole is called the Debye force.
Two randomly oriented dipoles: \(1/r^7\)
There's a statistical mechanics approach to computing the interaction between two systems that are dipoles with orientations that can move around randomly due to thermal fluctuations. This explained in Section 3.2.2 here:
Individually each object has zero dipole moment on average, but together they tend to line up, to reduce free energy. You again get a \(1/r^7\) force. This is called the Keesom force.
Two induced dipoles: \(1/r^7\)
Two initially spherically symmetric neutral atoms can also create dipole moments in each other due to quantum effects! Again this produces a \(1/r^7\) force. A quantum-mechanical derivation of this force law can be seen here:
Further reading
What I've described so far is just the tip of the iceberg when it comes to van der Waals forces. One has to get a lot more detailed to make quantitative predictions. For a really good account, after reading the above articles, dive into this:
June 16, 2024
We learned about the Sausage only after 2014, when an EU-run satellite called Gaia began carefully measuring the velocities of many stars in the Milky Way. Many dwarf galaxies that collided with the Milky Way were already known. But the Sausage was hard to detect until we got good at watching stars move by repeatedly measuring their position.
June 17, 2024

June 18, 2024

June 19, 2024
You can read about trihelium here, though I must sadly admit the more official name is the 'helium trimer':
Here's one interesting thing: you shouldn't imagine it as an equilateral triangle! Instead, the three atoms move around to form randomly shaped triangles. It might be a chaotic 3-body system, tamed somewhat by quantum mechanics.
June 21, 2024

Electrons are referred to as negative because of their behavior in an electric field. In an electric field, an electron will move from the negative pole to the positive pole, giving it a negative charge by convention.
"If we re-designate all positive electric charges as negative and vice versa, while keeping their absolute value, the resulting physics would be the same. So exact choice is merely a matter of convention."
In the quantum theory of elementary particles (in a sense of irreducible representation of Poincare group with mass \(m\) and spin \(s\)) if some operator \(Q\) of internal symmetry commutes (like electric charge charge) with Hamiltonian \(H\)....
June 27, 2024
I've been offered, and have accepted, a job at the University of Edinburgh. It's called the Maxwell Fellow in Public Engagement. It's
a 5-year, part-time, Reader-level appointment held jointly between the Schools of Mathematics and Physics and Astronomy. The primary responsibility of the fellowship holder is to generate public engagement with fundamental concepts and applications of mathematics and physics, reaching a global and diverse audience. The holder of the Fellowship will also be expected to pursue a program of original research in mathematics, theoretical physics or their applications, and to contribute to teaching in the Schools.
If we succeed in getting a visa — as required for this job, and likely to happen — my wife Lisa and I will need to be in the UK at least 180 days a year. But job is part-time, so we can continue to spend some time in California.
June 29, 2024
In the Big Bang, about 1/4 of the matter in the Universe fused into helium. Unfortunately, very little turned into heavier elements. As far as I can tell, it took about 10 billion years for pathetic little stars to crank out enough carbon, oxygen and other good stuff to support life. By the time we showed up, the party was almost over: the peak of star formation was long past, and the accelerating expansion of the Universe had begun. In another 10 billion years, the portion of the Universe we can still reach by moving slower than light will shrink by 80%. If so-called intelligent life wants to spread across the Universe, it had better get its ass in gear.
For my July 2024 diary, go here.
© 2024 John Baez
baez@math.removethis.ucr.andthis.edu
home