

A copy of this print was sold by Fuji Arts, and they wrote:
Takeji Asano - Born in Kyoto, Takeji Asano worked in both the shin-hanga and sosaku hanga Japanese woodblock print traditions. He studied Western and Japanese painting, and became interested in woodblock prints after taking a class with Hiratsuka Un'ichi, one of the founders of the sosaku hanga or creative print movement. In 1929, he helped form the Kyoto Creative Print Society. After WWII, he created many woodblocks of scenery and famous sites in and around Kyoto in various seasons. In addition to designing shin-hanga series for Uchida and Unsodo, he also published his own works. His colorful sosaku hanga woodblocks, self-carved and self-printed, have a real graphic appeal, with bold line work, sweeping views, and handsome compositions. Asano's prints are a great choice for the modern collector, and make attractive framed displays.Comments - Interesting view of a farmer making his way through a grove of bamboo in Saga, carrying a hoe over his shoulder. The tall stalks tower above him, casting shadows across the path. A fence and oranges lilies frame the scene in the foreground. A handsome design.
See my October 1, 2021 entry for another beautiful print by Takeji Asano. Bamboo groves are also beautiful in real life:

November 2, 2021
Here's the Center for Hellenic Studies, where Lisa is working until
December 16th. We are living next door. It's a very quiet refuge in
Washington D.C.


In September 1859 telegraph systems failed all over Europe and North America, in some cases giving people electric shocks. Telegraph pylons threw sparks. The northern lights were so bright miners got up early, thinking it was dawn.
This was the Carrington Event.
The Carrington Event was a geomagnetic storm more powerful than any since... though an equally big one missed the Earth in 2012. If one this big hit us now, it could cause a trillion dollars of damage, and it could take 4-10 years to recover!
Some earlier geomagnetic storms were even bigger. The Miyake Event, in 775 AD, created the largest spike in carbon-14 ever recorded. The Miyake event was about 10 times more powerful than the Carrington event... though it's hard to estimate these storms from geological data, and people argue about them.
So we will someday be hit by another Carrington-class storm — or worse.
This sketch, made by the astronomer Richard Carrington on September 1st, 1859, shows a huge sunspot at the time of the Carrington Event:
Here's a painting called Aurora Borealis, made by Edwin Church in 1865, perhaps inspired by the Carrington Event:

If a bunch of events each happen with probability \(p \lt 1\) and they're all 'independent' in the usual technical sense, there's a nonzero chance that none of them happen. But what if they're not all independent? Then Shearer's Lemma can help.
Let's think about it a little.
Take \(n = 1\): suppose we've got finitely many events, each independent of all but one other. Each happens with probability \(\lt p\). But the probability that none of them happens is zero. How small can we choose \(p\) to be?
Shearer's lemma says: no smaller than \(1/2\).
To prove this sort of thing, it helps to draw a graph. Draw the events as a finite set of dots. Draw an edge between dots when those events are dependent. In the example we're doing, the dots come in pairs connected by an edge, and 'loners' independent of all others.
In this example, the key is to think about one pair of dependent events. Each happens with probability \(\lt p\). But the probability that neither happens is zero. How small can we choose \(p\) to be?
Shearer's lemma says: no smaller than 1/2.
Can you see how to make it 1/2?
Here's how: you flip a fair coin and the two events are 'heads' and "tails". Each happens with probability 1/2, but the probability that neither happens is zero. (Don't let the coin land on its edge.)
With an unfair coin can make heads happen with probability \(\lt 1/2\), but then tails happens with probability \(\gt 1/2\) if we demand the probability neither event happens is zero. So \(1/2\) is the limit in this particular \(n = 1\) example, as Shearer's Lemma suggests.
I should try some \(n = 2\) examples, and draw a few graphs where each dot is connected to at most two others. But I'll let you do it.

Wikipedia gives a general proof of a famous weaker result, the Lovász local lemma. Check it out:
You can see how the number \(e\) shows up. It comes from
$$ 1/e \lt \left(\frac{d}{d+1}\right)^d $$
so you can get a stronger version of the Lovász local lemma
that looks more like Shearer's lemma just by not using this
inequality.
November 7, 2021
You can pack equal-sized discs in the plane with a density of at most about 0.9069, but equal-sized regular octagons with a density of only at most about 0.9062.
Which convex shape is the worst? Experts believe it's the regular heptagon. The densest known packing of these is shown above. Its density is about 0.89269.
But at least when I last checked, nobody could proved that the regular heptagon was the worst — the so-called 'pessimal packer'. Nobody could even prove the regular heptagon's densest packing is the one shown above!
However, it has been shown that the packing above is the densest for which the regular heptagons come in two bunches, each forming a lattice, one upside-down compared to the other.

In 1998 Thomas Hales solved the Kepler Conjecture, proving that this packing of spheres is as dense as possible. But his proof was 250 pages long, with 3 gigabytes of calculations. After 4 years, journal referees could only say they were "99% certain" his proof was right.
The journal published his paper, but Hales turned to giving a fully rigorous computerized proof of the Kepler Conjecture. He organized a team to do this... and they finished in 2014!
Then he wrote a grant proposal to prove the Reinhardt conjecture. This says that a certain octagon with rounded corners is the worst convex shape with central symmetry if you're trying to pack shapes densely.
Interestingly, the density of this packing doesn't change as the octagons roll around.
I don't know exactly how much progress Hales has made in proving Reinhardt's conjecture. He's written one paper about it, and I hear he's writing another. But in 2016, he and Wöden Kusner rigorously proved that this is the densest packing of regular pentagons:
I do know this: Hales and Kusner proved that the densest packing of regular pentagons has density \((5 - \sqrt{5})/3 \approx\) 0.92131067. Their proof is 60 pages not counting computer calculations, with about 100 lemmas. It's extremely complicated! These problems are hard.

Progress in so-called "fundamental" physics slowed to a crawl after about 1980, at least if you only count theories that get confirmation from experiment. I saw this clearly when I made a timeline of fundamental physics from 1900 to 2020 for a talk I gave last week.
But 'fundamental' physics — which I try to quickly define in my talk — is not necessarily the most important or best kind! Other kinds of physics are doing well now. For example, condensed matter physics is full of amazing new ideas testable by experiment.
For my talk go here:
Wow! Rare earth elements, or 'lanthanides', aren't really very rare. But only in 2011 was a bacterium found that requires rare earths to live. It even has a special protein for dealing with them, called 'lanmodulin'. And now scientists have used it to make a sensor.
The bacterium lives in bubbling hot mud in a volcano. It survives by metabolizing methane. It ues landmodulin to catalyze this process, and at the heart of landmodulin is a rare earth atom! And of the four lightest lanthanides will work: lanthanum (Ln), cerium (Ce), praseodymium (Pr) and neodymium (Nd). These are chemically very similar.
The next lanthanide, prometheum (Pm), is not found naturally on earth. Why? That's another story — a story about nuclear physics. The next three are also used by life, but only very slightly: samarium (Sa), europeum (Eu) and gadolinium (Gd). The rest, apparently not at all — but who knows?

The protein lanmodulin, used by some bacteria, binds to the light rare earths a hundred million times better than to other metals, like calcium. Scientists have now modified it, adding an amino acid called trypotphan, to make a molecule that glows when it encounters the heavier rare earth element terbium, which is used in cell phones:
If you want to learn a bit more about lanthanides in biology, this open-access article is great:
This work has reignited my interest in the chemistry of these bewilderingly similar elements, and why the first four are different from the rest. They are more common — indeed cerium, is over 5 times as abundant in the Earth's crust than lead, while neodymium and lanthanum are about 2.5 times as abundant, and praseodymium is just a bit behind lead.
While they're not lanthanides, the lighter elements scandium (Sc) and yttrium (Y) are chemically similar, and also considered rare earths. Does biology ever use these? Nobody knows!
But as someone once said, "life will find a way."
Random permutations are fascinating. I was surprised when I first learned that a randomly chosen permutation of a large finite set tends to have a few big cycles. There's about a 69.3% chance that it has one giant cycle containing over half the elements!
This is not hard to show. You just need to compute the probability that a random permutation of an \(n\)-element set has a cycle of length \(k\), for each choice of \(k \gt n/2\). It can have at most cycle of length \(\gt n/2\), so then you can add up these probabilities and get the probability of a giant cycle.
So, how many permutations of an \(n\)-element set have a cycle of length \(k \gt n/2\)?
There are \({n \choose k}\) choices of which points lie on this cycle, \((k-1)!\) cyclic orderings of these points, and \((n-k)!\) permutations of the remaining points. Multiply these numbers: you get \(n!/k\).
So, when \(k \gt n/2\), the probability that a random permutation of an \(n\)-element set has a cycle of length \(k\) is just \(1/k\). Amazingly simple!
If we sum up these probabilities over all \(k\) between \(n/2\) and \(n\), we get about \(\ln 2\), which is about \(0.693\).
For more fun along these lines, see:

As the chlorophyll wanes, now is the heyday of the xanthophylls, carotenoids and anthocyanins. These contain carbon rings and chains whose electrons become delocalized... their wavefunctions resonating at different frequencies, emitting yellow, orange and red photons!
Yes, it's fall in Washington DC. I'm enjoying it.









I wrote about two xanthophylls in my May 27, 2014 entry: I explained how they get their color from a chain of carbons with conjugated double bonds. I discussed chlorophyll, which also has such a chain, in my May 29th entry. I wrote about some carotenoids in my July 2, 2006 entry: these too have long chains of carbons with conjugated double bonds.
I haven't discussed anthocyanins yet! These have rings rather than chains of carbon. They are often blue or purple, but they contribute to the color of many red leaves:
Click on these two graphics for more details! I got them from a website called Science Notes, and it says:
Some leaves make flavonoids. Anthocyanins are flavonoids which vary in color depending on pH. Anthocyanins are not usually present in leaves during the growing season. Instead, plants produce them as temperatures drop. They acts as a natural sunscreen and protect against cold damage. Anthocyanins also deter some insects that like to overwinter on plants and discourage new seedlings from sprouting too close to the parent plant. Plants need energy from light to make anthocyanins. So, vivid red and purple fall colors only appear if there are several sunny autumn days in a row.This raises a lot of questions, like: how do anthocyanins protect leaves from cold, and why do some leaves make them only shortly before they die? Or are they there all along, hidden behind the chlorophyll? Maybe this paper would help:




Each element of the homotopy group \(\pi_k(S^n)\) is basically a way of wrapping a \(k\)-dimensional sphere around an \(n\)-dimensional one. I conjecture that there are never exactly \(5\) ways.
Unlike Fermat, I won't pretend I have a truly remarkable proof which this diary entry is too small to contain.
More strongly, I conjecture that \(\pi_k(S^n)\) never has a prime number of elements, except for the primes \(2\) and \(3\).
My evidence for these conjectures is quite weak — some empirical evidence and the known role that primes play in homotopy groups of sphere. But I hope trying to prove or disprove these conjectures will lure the experts into new feats of ingenuity.

To be a bit more precise, \(\pi_k(S^n)\) is the set of continuous maps from the \(k\)-sphere to the \(n\)-sphere, where we count two maps as the same if we can continuously deform one to another. For \(k \gt 0\) this is an abelian group. Sometimes it's infinite, but we know exactly when: when \(k = n\), and when \(n\) is even and \(k = 2n - 1\).
This table by Richard Wong shows these patterns — and it begin to show how complicated these groups can get:
It's hard to compute the group \(\pi_k(S^n)\), and people use clever methods to do it. It's a bit easier in the 'stable range' where \(2n \gt k + 1\). In this case if you add \(1\) to both \(k\) and \(n\) the group doesn't change. In other words, it depends only on the difference \(i = k - n\). It's called \(\pi_i^S\).
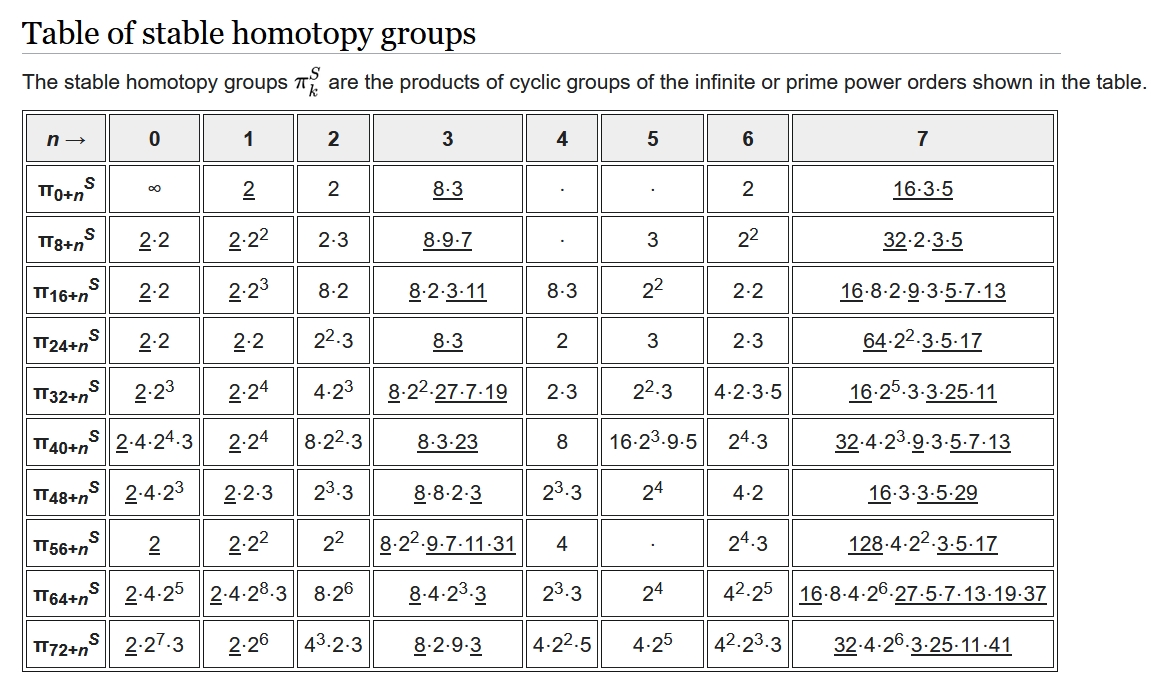
This chart takes a bit of work to decipher, but if you work you can see that \(\pi_{60}^S \cong \mathbb{Z}_4\). Thus, \(\pi_k(S^n) \cong \mathbb{Z}_{4}\) if \(k - n = 60\) and \(2n \gt k + 1\). Putting these together we get \(n \gt 61\). So, \(\pi_{122}(S^{62}) \cong \mathbb{Z}_4\).
The groups \(\pi_k^S\) follow intricate patterns involving prime numbers. Every finite abelian group is a product of cyclic groups whose orders are powers of primes. If we focus on the prime \(2\), the groups \(\pi_k^S\) follow this extremely complicated pattern (from Hatcher):

For the prime 3, we get this pattern:
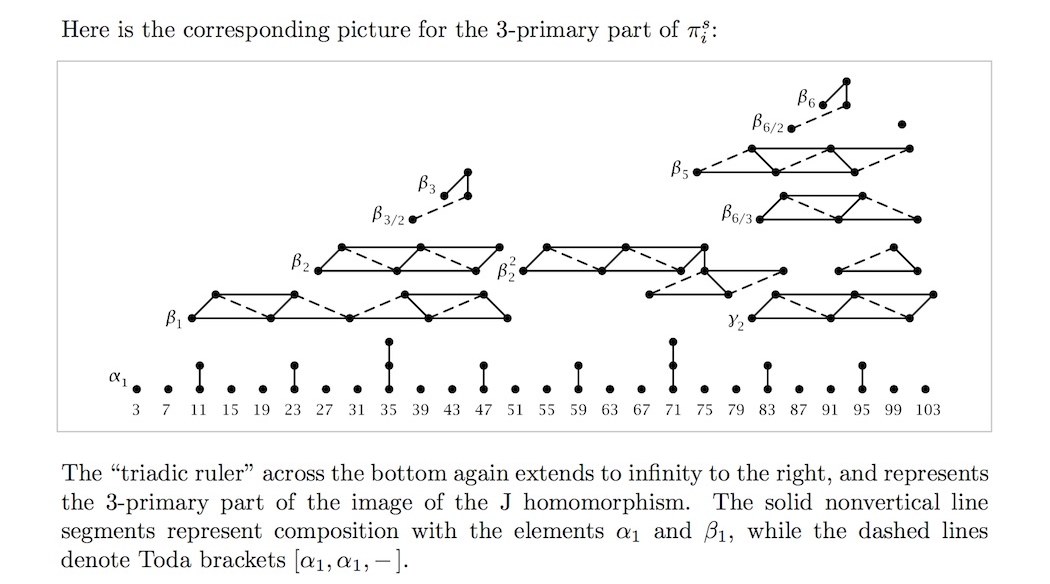
For the prime \(5\) the pattern is a bit simpler, which has let people go farther. But still it's full of complications — there's no simple formula, as far as anyone knows.
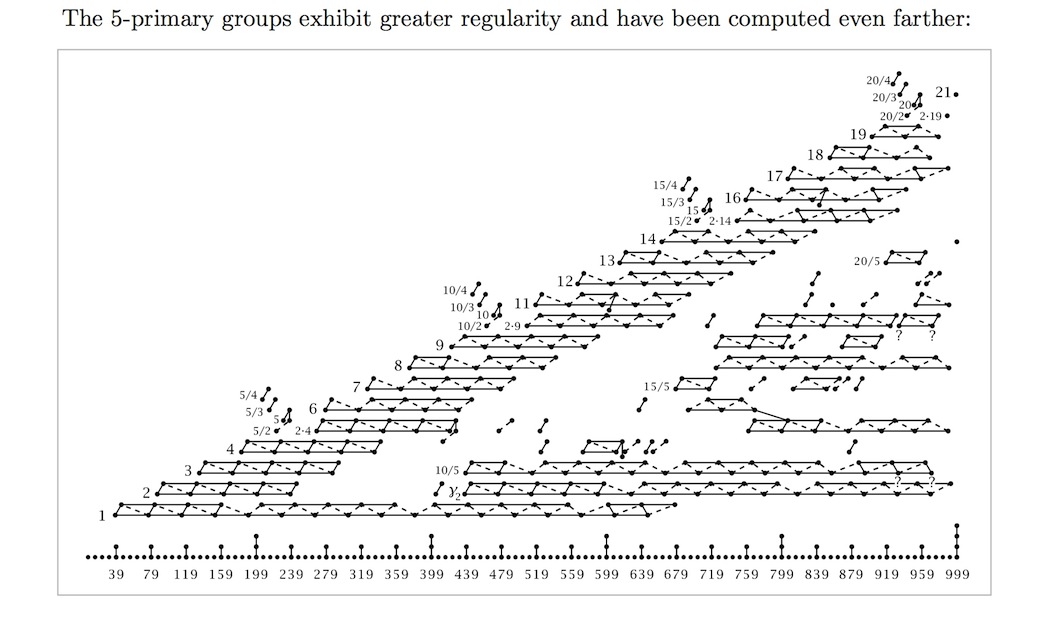
Perhaps experts know enough about \(2, 3,\) and \(5\) parts of the stable homotopy groups of spheres to show — with hard work? — that these groups can never have just \(5\) elements. (They can have \(2^4 \times 3 \times 5 = 240\) elements, etc.) That would prove Conjecture 1 'in the stable range'.
Tackling Conjecture 1 outside the stable range seems a lot harder, and Conjecture 2 even harder. They could be false! Maybe computing more homotopy groups of spheres will yield a counterexample. If anyone knows how to make progress, I'd like to hear about it. You can contribute to this discussion:
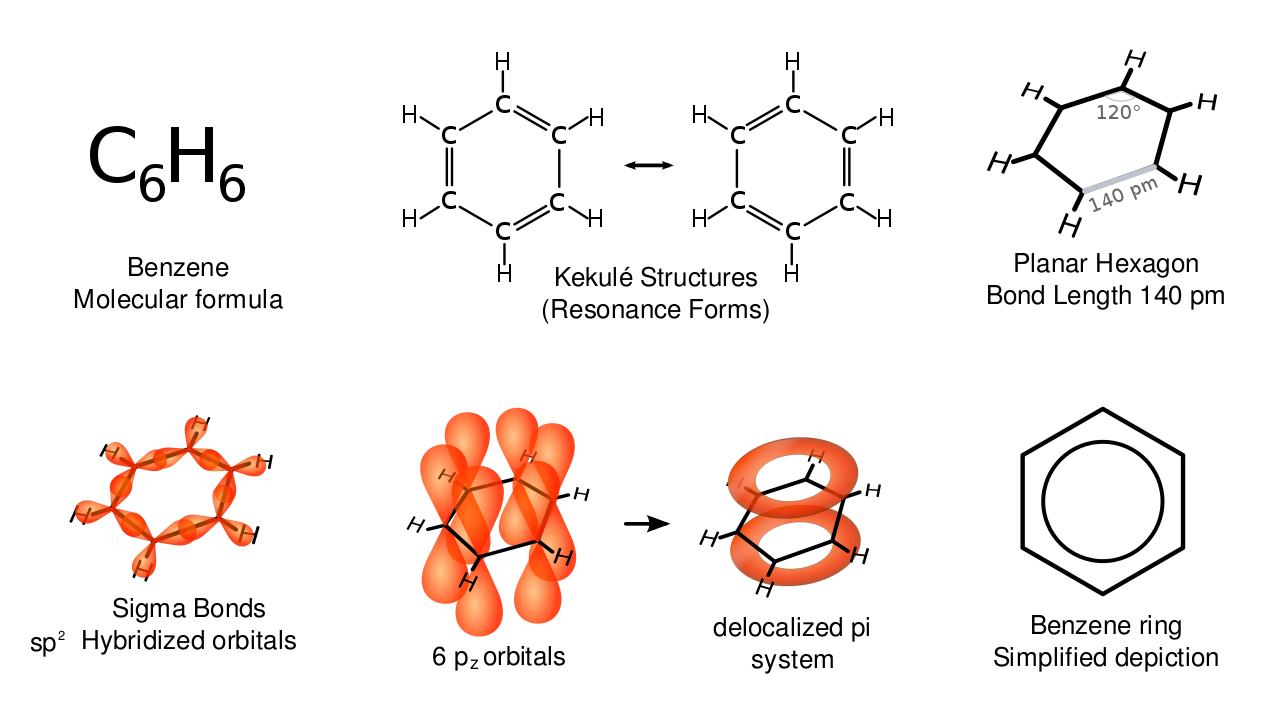
The structure of benzene is fascinating. Look at all these different attempts to depict it! Let me tell you a tiny bit of the history.
In 1865, August Kekulé argued that benzene is a ring of carbon atoms with alternating single and double bonds. Later, at a conference celebrating the 25th anniversary of this discovery, he said he realized this after having a daydream of a snake grabbing its own tail.
Kekulé's model was nice, because before this it was hard to see how 6 carbons and 6 hydrogens could form a reasonable molecule with each carbon having 4 bonds and each hydrogen having one. But this model led to big problems, which were only solved with quantum mechanics.
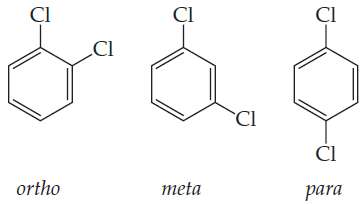
If benzene looked like Kekulé's model, there would be 4 ways to replace two hydrogens with chlorine! You could have two chlorines next to each other with a single bond between them as shown here... or a double bond. But there aren't 4, just 3.
In 1872 Kekulé tried to solve this problem by saying benzene rapidly oscillates between two forms. Below is his original picture of those two forms. The single bonds and double bonds trade places.
But there was still a problem: benzene has less energy than if it had alternating single and double bonds.
The argument continued until 1933, when Linus Pauling and George Wheland used quantum mechanics to tackle benzene. Here's the first sentence in their paper:
As you can see, there were models much stranger than Kekulé's.
What was Pauling and Wheland's idea? Use the quantum superposition principle! A superposition of a live and dead cat is theoretically possible in quantum mechanics... but a superposition of two structures of a molecule can have lower energy than either structure alone, and then this is what we actually see! Here's what Pauling said later, in 1946:
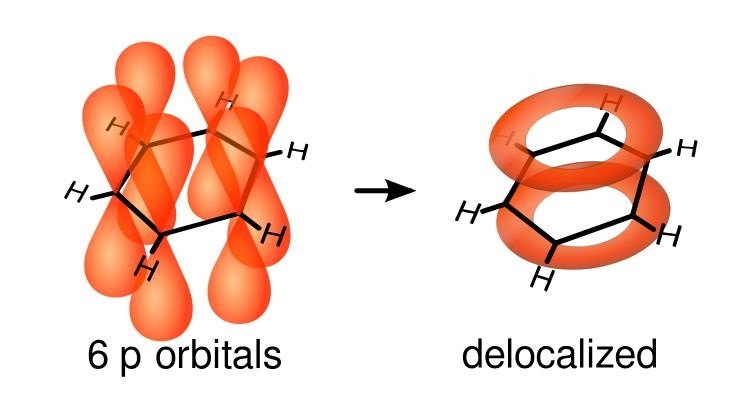
But in reality, benzene is much subtler than just a quantum superposition of Kekulé's two structures. For example: 6 of its electrons become "delocalized", their wavefunction forming two rings above and below the plane containing the carbon nuclei! So I'm really just starting this story, but I'm gonna quit here — for now at least.
Huh? I knew about benzene's ring of 6 carbons, but not tropylium, a positively charged ion with a ring of 7.
Chemistry is math where the objects have strong personalities. You're
just finding solutions of an equation — but some are red, some stink,
etc.
November 23, 2021
There are infinitely many ways an electron (shown as a straight line here) can emit virtual photons (wiggly lines), which in turn split into virtual electron-positron pairs, and so on. All these affect the electron's mass.
There 104 ways where the picture has 4 loops.
By attaching another photon line to those pictures, Stefano Laporta found all 891 diagrams with 4 loops where an electron absorbs a photon. He grouped them into 25 groups, shown here:
An electron is a little magnet. He computed the effect of all 891 diagrams on the strength of that magnet.
He showed the effect of these 891 diagrams on the magnetism of the electron is about $$ -1.912 \cdot \left(\frac{\alpha}{\pi}\right)^4 $$ where \(\alpha\) is the fine structure constant.
But since he's a bit obsessive, he computed this number to 1100 digits of accuracy!
But Laporta developed a lot of clever mathematics to do this calculation. He did something much more efficient and interesting than computing 891 separate integrals! By grouping them, he was able to express them as rational linear combination of numbers called 'periods': values of the Riemann zeta function, elliptic integrals, harmonic polylogarithms, and 6 new numbers that had never been studied. For some of these numbers, algorithms were already known that could efficiently compute them to arbitrary precision. For others he needed to develop algorithms of this sort.
On Twitter, Giovanni Bracchi wrote:
Laporta basically disappeared shortly after proposing this topic to one of his professors for a master's thesis, then showed up in their office two years later with the calculations.Federico Capoani added:
The professor had just assumed he'd moved on to other things – instead he had found many shortcuts that allowed some of these terms to be derived from other terms, simplifying matters greatly.Adding to the story: Laporta's computations are done on two old desktop computers that are found in a shared office at Bologna university used by master students writing their thesis. There is just a post-it on the monitor where it's written "g-2. Don't switch off please."
For more of the story, try this:
For the actual paper, go here:
If you spill salt into a gas flame, it turns yellow. That's from sodium.
If you look very carefully at this light, like with a spectroscope, you'll see it has two slightly different colors of yellow. You can see those two yellow spectral lines above.
And if you put glowing sodium in a magnetic field, these difference between these two shades of yellow increases!
What's going on?
Sodium has 11 electrons:
But it can do this in two ways! So when it jumps back down, it emits two colors of yellow light.
Why are there two ways? Time for a little quantum mechanics:
Electrons in orbitals which aren't spherically symmetric orbit around the nucleus and create a magnetic field. But also electrons have spin, which makes them into little magnets. The combination of these two facts causes 'spin-orbit interactions'. An electron has more energy if its spin is lined up with the magnetic field.
So, when the the electron spins the same way as it orbits around the nucleus, it has a wee bit more energy than when it spins the opposite way. So, when it jumps back down, it releases a slightly more energetic photon... with a slightly greener shade of yellow!
If we now put the sodium in an extra magnetic field, adding to the magnetic field made by the orbiting electron, this effect gets stronger! So the difference in colors gets bigger. This is the 'anomalous Zeeman effect'.
So if this Thanksgiving you're cooking on a gas stove, or eating with candlelight, put a bit of salt in the flame and check out the photons with wavelengths 589 and 589.6 nanometers!
I get a lot of pictures from different sources and don't always properly credit them, though you can usually see the source if you click on a picture here. This time I really have to thank Hyperphysics. You can have lots of fun if you start on their 'sodium doublet' page and explore concepts by clicking links:
By the way: can you actually see the difference between the two yellows with the naked eye? Apparently not quite!
The good news: human sensitivity to slight differences in wavelength is at its best in the yellow range.
The bad news: it's \(1\)-\(2\) nanometers there, while these spectral lines differ by just \(0.6\) nanometers.
Perhaps a few 'super-seers' can tell the difference. Someone should
do the experiment!
November 26, 2021

Josephine Baker will be the first Black woman buried in the Panthéon in Paris. Born in St. Louis, she sang in Paris, became a French citizen in 1937, joined the French resistance, spied on the Nazis, and carried intelligence in invisible ink on her sheet music while touring.

After the war she was decorated by De Gaulle. When she returned to New York in 1950, she was refused reservations at 36 hotels because she was Black. She complained, refused to play for segregated audiences, and was put on a watch list by the FBI.

She was the only official woman speaker at Martin Luther King's March on Washington in 1963. She wore her Free French uniform. In her speech, she said:
I have walked into the palaces of kings and queens and into the houses of presidents. And much more. But I could not walk into a hotel in America and get a cup of coffee, and that made me mad. And when I get mad, you know that I open my big mouth.

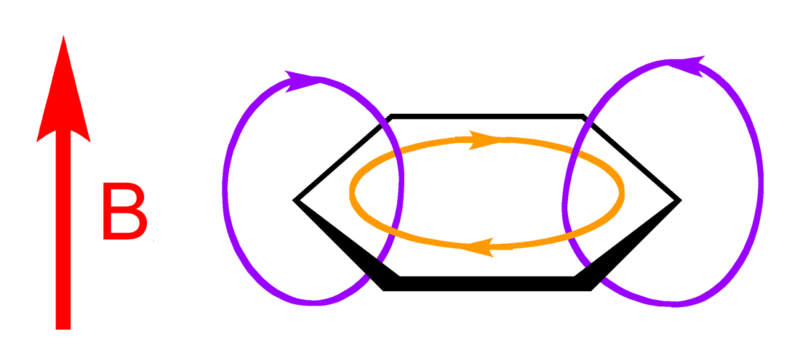
What does this current loop look like, exactly? To understand this, you have to know that the 6 smeared out or 'delocalized' electrons lie above and below the plane of the benzene molecule. They come from the p orbitals of the carbon atoms, which point up and down.
So, if you compute the electric current above or below the plane of the benzene molecule, it goes around and around like this:
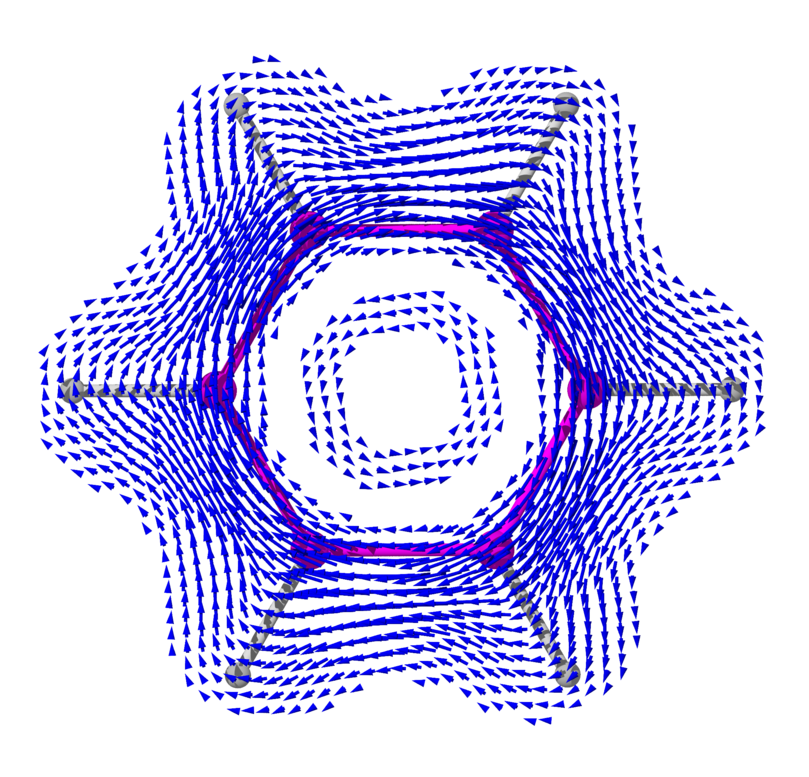
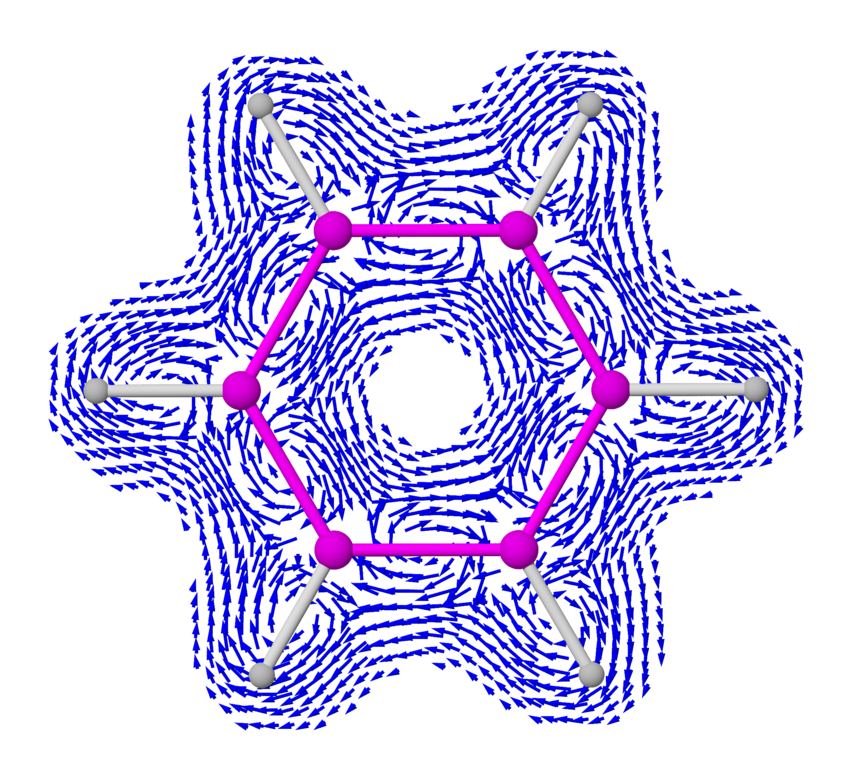
Outside the benzene molecule it points the same way as the externally imposed magnetic field, reinforcing it. So, a magnetic field that is strengthened when it goes through benzene. This is called 'antishielding' — or 'deshielding' in this picture from Organic Spectroscopy International:
Organic compounds with rings containing delocalized electrons are called 'aromatic': benzene is the simplest. The effect I'm talking about is called an 'aromatic ring current'.
I got some pictures from this Wikipedia article:
including the pictures of current vector fields in benzene, created
by 'Hoferaanderl'.
November 28, 2021
The day before yesterday we had a nice Thanksgiving with other people
living and working at the Center for Hellenic Studies. Lisa cooked a
turkey and I cooked sweet potatoes. We took them, and a couple
bottles of wine, next door to Suzanne Lye's house. She had bought a
bunch of Malaysian food and a bunch of desserts: an apple pie, an
apple tart, a pumpkin pie, a pecan pie and an apple crisp. Angela
Cinalli brought pasta. Karolina Sekita brought the makings for
negronis: gin, campari and vermouth.
Yesterday, Lisa's guqin teacher John Thompson and his wife Suzanne visited. We went on a walk to Compass Coffee. Then John gave Lisa a lesson, and then we all went to dinner at Bistrot Lepic, a French restaurant on Wisconin Avenue that we like. We walked there and back — very cold on the way back. All in all, we walked seven miles!
As the leaves thin out, a few small trees across the way are still loaded with berries, which are attracting a lot of hungry birds.








The transition metals, shown in salmon here, are more complicated than lighter elements.
Why?
Because they're the first whose electron wavefunctions are described by quadratic functions of \(x,y,\) and \(z\) — not just linear or constant. These are called 'd orbitals', and they look sort of like this:
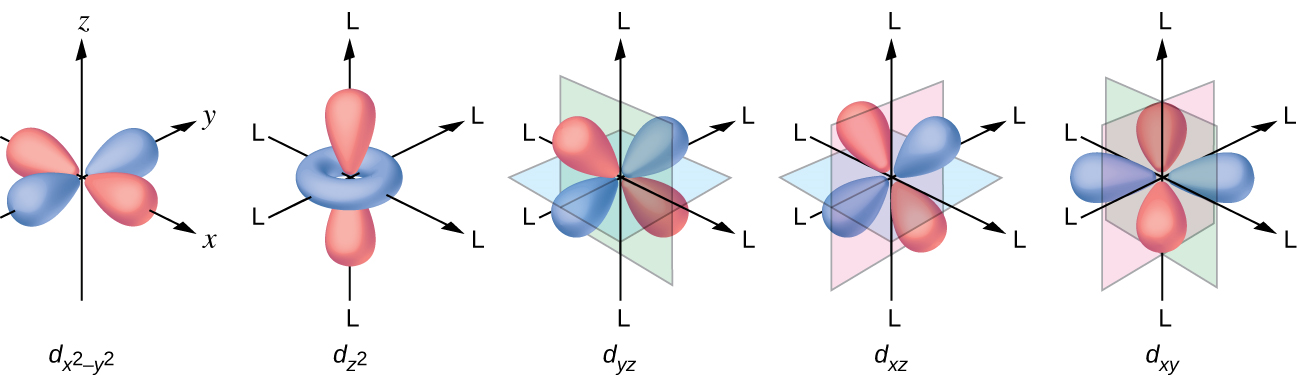
More precisely: the wavefunctions of electrons in atoms involve a 'spherical harmonics', functions on the sphere that can be described using polynomials in \(x,y,z\). The jargon goes like this:
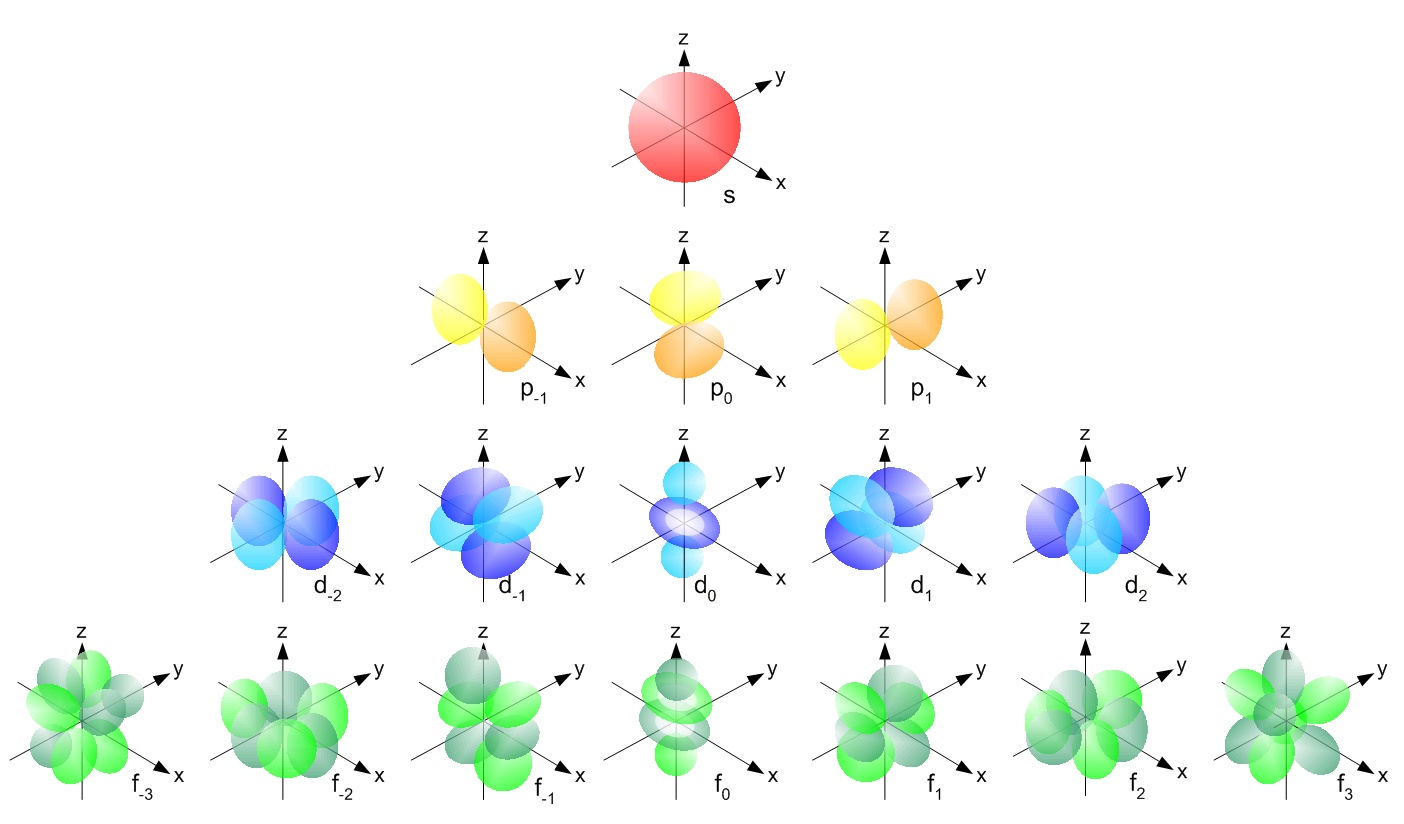
To be even more precise, a spherical harmonic is an eigenfunction of the Laplacian on the sphere. Any spherical harmonic can be written as the restriction to the sphere of some homogeneous polynomial in \(x,y,z\) whose Laplacian in 3d space is zero. This can be constant, linear, etc.
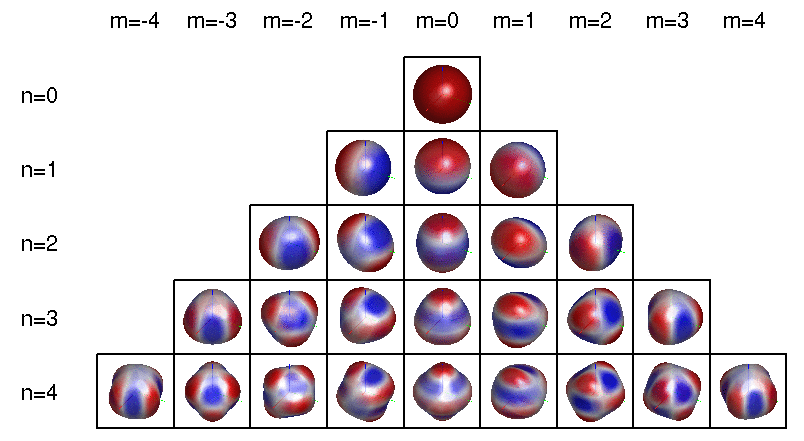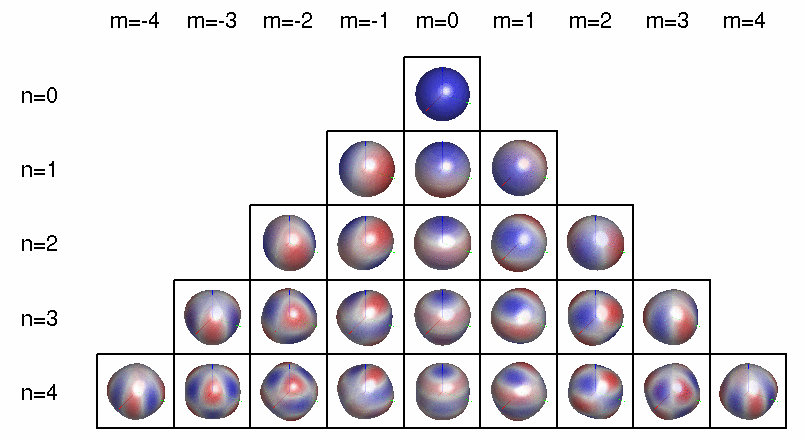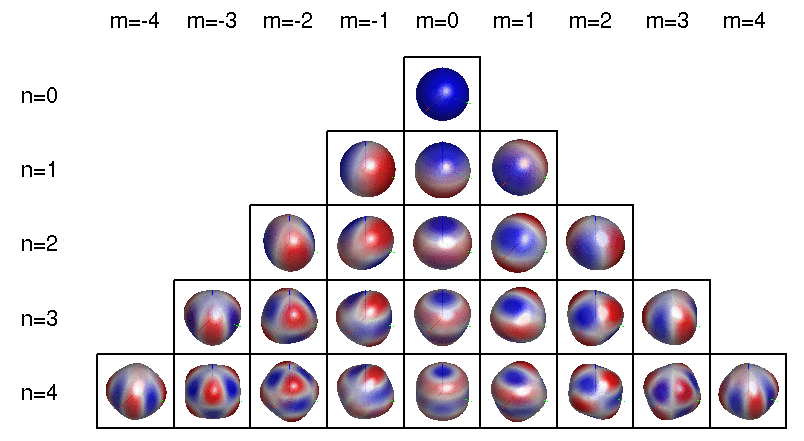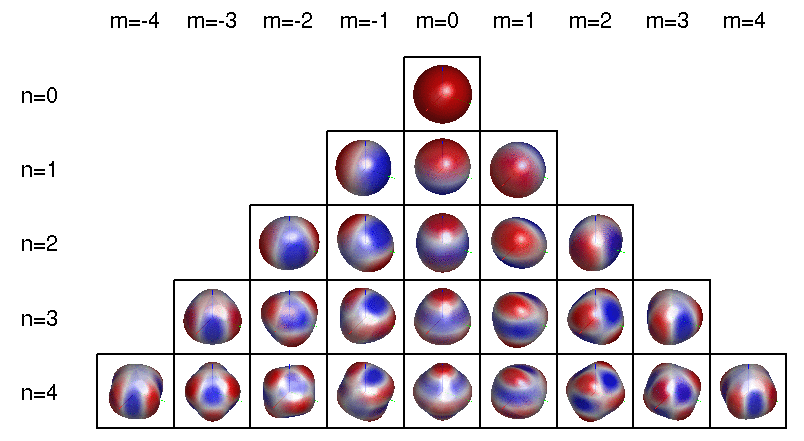
The dimension of the space of spherical harmonics goes like \(1, 3, 5, 7, \dots\) as we increase the degree of the polynomial starting from 0:
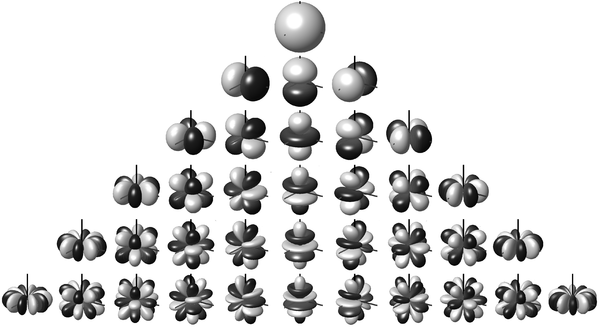
The transition metals are the first to use the d orbitals!

I guess the d orbital called \(d_{z^2}\) really comes from the function \(z^2 - x^2 - z^2\), since that has vanishing Laplacian. Note also that once we've chosen \(xy, xz, yz, x^2 - y^2, z^2 - x^2 - y^2 \) as our 5 homogeneous quadratic polynomials with vanishing Laplacian, we don't need \(x^2 - z^2\) and \(y^2 - z^2\), since they're linearly dependent. There's nothing wrong with them: they're just as important physically. We're just chosing a basis of 5 such functions.