This picture by Roice Nelson shows a remarkable structure: the hexagonal tiling honeycomb.
What is it? Roughly speaking, a honeycomb is a way of filling 3d space with polyhedra. The most symmetrical honeycombs are the 'regular' ones. For any honeycomb, we define a flag to be a chosen vertex lying on a chosen edge lying on a chosen face lying on a chosen polyhedron. A honeycomb is regular if its geometrical symmetries act transitively on flags.
The most familiar regular honeycomb is the usual way of filling Euclidean space with cubes. This cubic honeycomb is denoted by the symbol {4,3,4}, because a square has 4 edges, 3 squares meet at each corner of a cube, and 4 cubes meet along each edge of this honeycomb. We can also define regular honeycombs in hyperbolic space. For example, the order-5 cubic honeycomb is a hyperbolic honeycomb denoted {4,3,5}, since 5 cubes meet along each edge:
Coxeter showed there are 15 regular hyperbolic honeycombs. The hexagonal tiling honeycomb is one of these. But it does not contain polyhedra of the usual sort! Instead, it contains flat Euclidean planes embedded in hyperbolic space, each plane containing the vertices of infinitely many regular hexagons. You can think of such a sheet of hexagons as a generalized polyhedron with infinitely many faces. You can see a bunch of such sheets in the picture:
The symbol for the hexagonal tiling honeycomb is {6,3,3}, because a hexagon has 6 edges, 3 hexagons meet at each corner in a plane tiled by regular hexagons, and 3 such planes meet along each edge of this honeycomb. You can see that too if you look carefully.
A flat Euclidean plane in hyperbolic space is called a horosphere. Here's a picture of a horosphere tiled with regular hexagons, yet again drawn by Roice:
Unlike the previous pictures, which are views from inside hyperbolic space, this uses the Poincaré ball model of hyperbolic space. As you can see here, a horosphere is a limiting case of a sphere in hyperbolic space, where one point of the sphere has become a 'point at infinity'.
Be careful. A horosphere is intrinsically flat, so if you draw regular hexagons on it their internal angles are $$ 2\pi/3 = 120^\circ $$ as usual in Euclidean geometry. But a horosphere is not 'totally geodesic': straight lines in the horosphere are not geodesics in hyperbolic space! Thus, a hexagon in hyperbolic space with the same vertices as one of the hexagons in the horosphere actually bulges out from the horosphere a bit — and its internal angles are less than \(2\pi/3\): they are $$ \arccos\left(-\frac{1}{3}\right) \approx 109.47^\circ $$ This angle may be familar if you've studied tetrahedra. That's because each vertex lies at the center of a regular tetrahedron, with its four nearest neighbors forming the tetrahedron's corners.
It's really these hexagons in hyperbolic space that are faces of the hexagonal tiling honeycomb, not those tiling the horospheres, though perhaps you can barely see the difference. This can be quite confusing until you think about a simpler example, like the difference between a cube in Euclidean 3-space and a cube drawn on a sphere in Euclidean space.
Back in 2022, James Dolan and I conjectured such a description, which takes advantage of the picture of Minkowski spacetime in terms of 2×2 matrices. And this April, working on Mathstodon, Greg Egan and I proved this conjecture!
I'll just describe the basic idea here, and refer you elsewhere for details.
The Eisenstein integers \(\mathbb{E}\) are the complex numbers of the form $$ a + b \omega $$ where \(a\) and \(b\) are integers and \(\omega = \exp(2 \pi i/3)\) is a cube root of 1. The Eisenstein integers are closed under addition, subtraction and multiplication, and they form a lattice in the complex numbers:
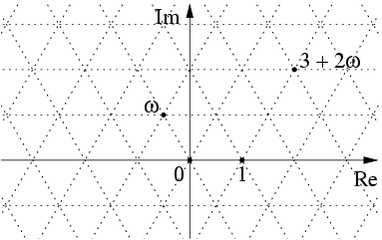
Similarly, the set \(\mathfrak{h}_2(\mathbb{E})\) of 2×2 hermitian matrices with Eisenstein integer entries gives a lattice in Minkowski spacetime, since we can describe Minkowski spacetime as \(\mathfrak{h}_2(\mathbb{C}).\)
Here's the conjecture:
Conjecture. The points in the lattice \(\mathfrak{h}_2(\mathbb{E})\) that lie on the hyperboloid \(\mathcal{H}\) are the centers of hexagons in a hexagonal tiling honeycomb.
Using known results, it's relatively easy to show that there's a hexagonal tiling honeycomb whose hexagon centers are all points in \(\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}.\) The hard part is showing that every point in \(\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}\) is a hexagon center. Points in \(\mathfrak{h}_2(\mathbb{E}) \cap \mathcal{H}\) are the same as 4-tuples of integers obeying an inequality (the \(\mathrm{tr}(A) > 0\) condition) and a quadratic equation (the \(\det(A) = 1\) condition). So, we're trying to show that all 4-tuples obeying those constraints follow a very regular pattern.
Here are two proofs of the conjecture:
Here instead of the Eisenstein integers we should use the Gaussian integers, \(\mathbb{G}\), consisting of all complex numbers $$ a + b i $$ where \(a\) and \(b\) are integers.
Conjecture. The points in the lattice \(\mathfrak{h}_2(\mathbb{G})\) that lie on the hyperboloid \(\mathcal{H}\) are the centers of squares in a square tiling honeycomb.
(By now this has been proved by Mist.)
I'm also very interested in how these results connect to algebraic geometry! I explained this in some detail here:

The press likes to talk about problems, so it paints everything as a problem. But some problems are better than other problems.
From here:
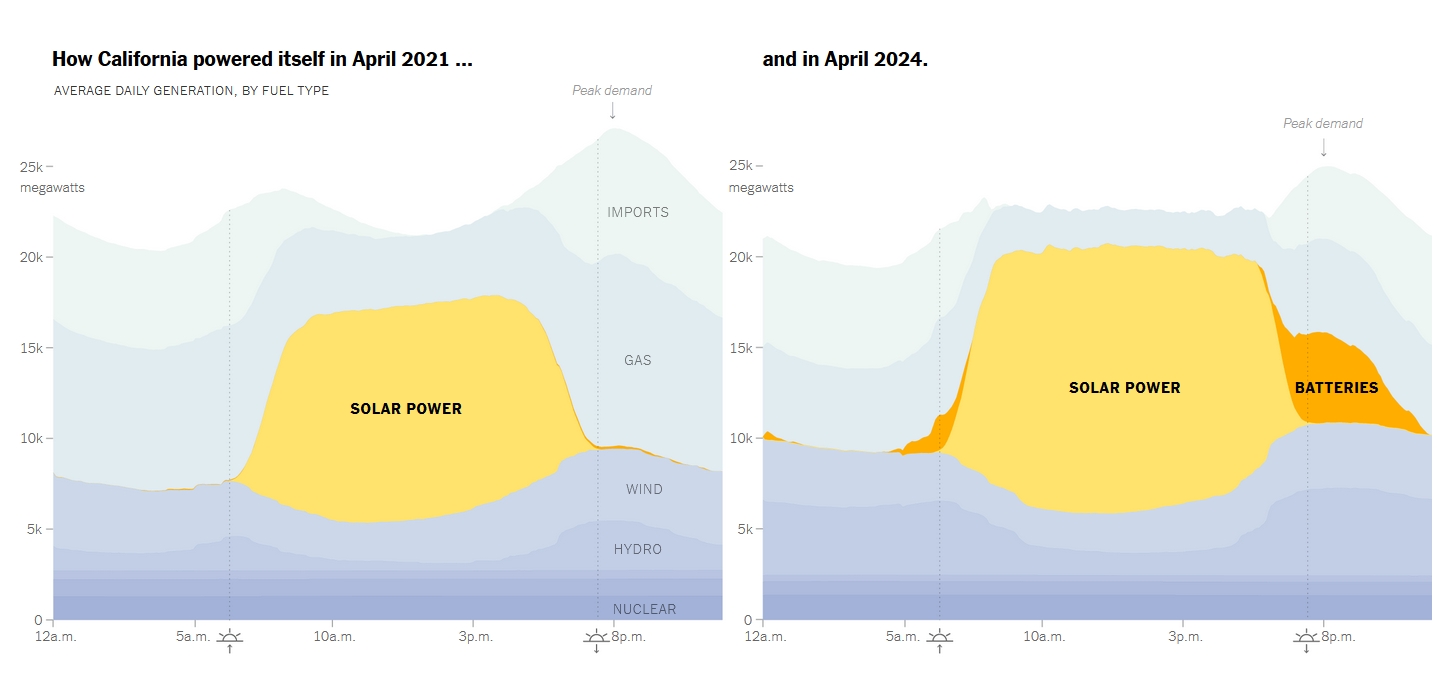
Since 2020 California has installed more batteries than anywhere in the world except China. Peak power usage comes between 7 and 10 pm, so solar power must be stored to handle this demand. It's starting to happen!
This year battery storage is expected to nearly double in the US, with the biggest growth in Texas, California and Arizona.
From here:
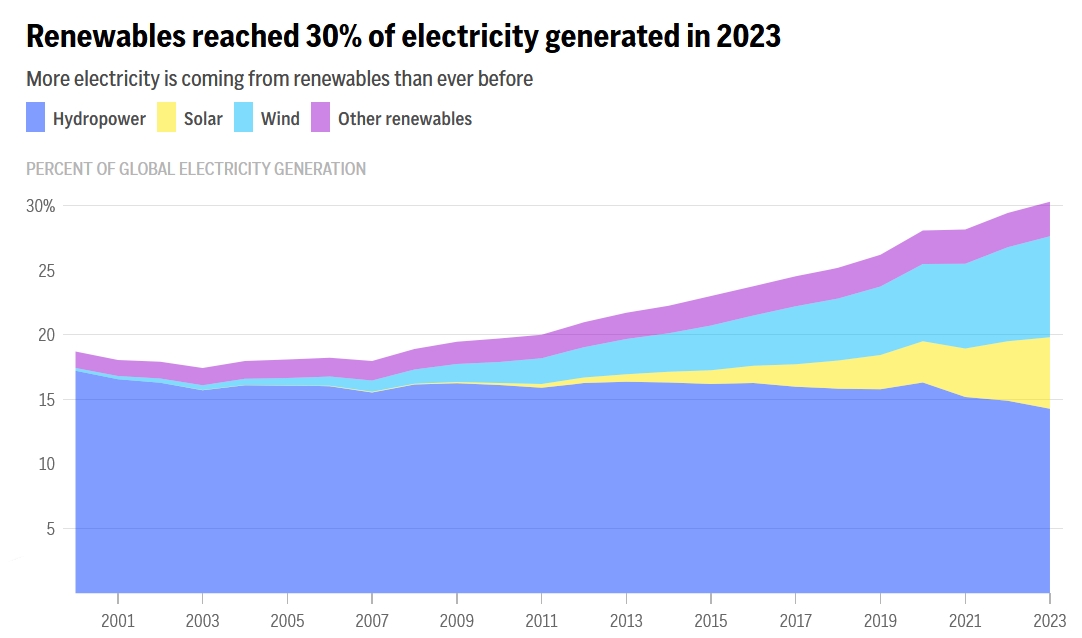
Last year, for the first time, 30% of electricity produced worldwide was from renewable sources. Wind and solar are growing. But notice that the biggest is hydroelectric, and it's going down! One reason is droughts in India, China, North America and Mexico. Climate change is causing droughts.
We're in a race against time. But at least we're running.
From here:
This is an ORC: an "odd radio cluster". It's a faint circle of radio emissions surrounding a distant galaxy. 5 ORCs have been found. This one is about a million light years in diameter, roughly 10 times the size of a galaxy like ours. So it was probably formed by some sort of explosion, and took a long time to get this big. But the details remain a mystery!
Astronomers have just discovered that one ORC is emitting X-rays. So at least in that one ORC, the diffuse gas must be hot: about 8 million Celsius.
Here are some theories of what an ORC might be:
But we can still have some fun. So watch an animated gif of what the birth of an ORC might look like:
This illustrates a possible scenario for the formation of an ORC: some sort of explosion in the host galaxy, producing a shock wave that expanded outwards for a billion years.
For more on ORCs, try these:

Costa Talalaev gave me a fractal: a 3-dimensional Sierpinski gasket!
He made it using the 3d printer at the Hacklab, a makerspace here in
Edinburgh. It was a bit hard to make since it's held together only at
tiny spots. He had to build something with more plastic, a kind of
scaffolding, and then tear that off. The end result is very light yet
sturdy.
May 12, 2024
We were listening to bouzouki music, and the conversation naturally turned to bazookas. It turns out that there's also bazooka music!
The comedian Bob Burns invented a horn-like instrument in the 1910s — he's shown with it above. It actually caught on in jazz in the 1930s. Someone jokingly called it the "bazooka" after the word "bazoo", which was slang for "mouth".
Later, in World War II, "bazooka" became the name for a new American anti-tank weapon, because it looked like this instrument.
Ironically, the slang word "bazoo", for "mouth", probably came from the word "buisine", which was the name of a medieval trumpet! And that comes from "buccina", a brass horn used by the Roman army.
In case you're wondering, he word "bouzouki" is unrelated. It comes from the Turkish word "bozuk", meaning "broken" or "modified", which refers to a particular way of tuning a string instrument where the notes are not arranged from low to high.
May 17, 2024
The precise location of the boundary between the knowable and the unknowable is itself unknowable. But we do know some details about why this is true, at least within mathematics. It's being studied rigorously in a branch of theoretical computer science called 'meta-complexity theory'.
For some reason it's hard to show that math problems are hard. In meta-complexity theory, people try to understand why.
For example, most of us believe P ≠ NP: merely being able to check the answer to a problem efficiently doesn't imply you can solve it efficiently. It seems obvious. But despite a vast amount of work, nobody has been able to prove it!
And in one of the founding results of meta-complexity theory, Razborov and Rudich showed that if a certain attractive class of strategies for proving P ≠ NP worked, then it would be possible to efficiently crack all codes! None of us think that's possible. So their result shows there's a barrier to knowing P ≠ NP.
I'm simplifying a lot of stuff here. But this is the basic idea: they proved that it's probably hard to prove that a bunch of seemingly hard problems are really hard.
But note the 'probably' here! Nobody has proved we can't efficiently crack all codes. And this too, seems very hard to prove.
So the boundary between the knowable and unknowable is itself shrouded in unknowability. But amazingly, we can prove theorems about it!
Here's a nice article on this:

When Maxwell realized in 1862 that light consists of waves in the electromagnetic field, why didn't anyone try to use electricity to make such waves right away? Why did Hertz succeed only 24 years later?
According to The Maxwellians:
Since he regarded the production of light as an essentially molecular and mechanical process, prior, in a sense, to electromagnetic laws, Maxwell could elaborate an electromagnetic account of the propagation of light without ever supposing that ether waves were produced purely electromagnetically.
In 1879, a physicist named Lodge realized that in theory one could make "electromagnetic light". But he didn't think of creating waves of lower frequency:
Send through the helix an intermittent current (best alternately reversed) but the alternations must be very rapid, several billion per sec.
He mentioned this idea to Fitzgerald, who believed he could prove it was impossible. Unfortunately Fitzgerald managed to convince Lodge. But later he realized his mistake:
It was FitzGerald himself who found the flaws in his "proofs." He then proceeded to put the subject on a sound theoretical basis, so that by 1883 he understood quite clearly how electromagnetic waves could be produced and what their characteristics would be. But the waves remained inaccessible; FitzGerald, along with everyone else, was stymied by the lack of any way to detect them.
In 1883, Fitzgerald gave a talk called "On a Method of Producing Electromagnetic Disturbances of Comparatively Short Wavelengths". But he couldn't figure out how to detect these waves. Hertz figured that out in 1886.
For much more on this, read:

When global warming gets bad enough to create millions of refugees, just imagine how nasty the EU and US will become. They may just send people out to the desert to die.
Oh wait, you don't have to imagine! It's happening already:
A year-long joint investigation by The Washington Post, Lighthouse Reports and a consortium of international media outlets shows how the European Union and individual European nations are supporting and financing aggressive operations by governments in North Africa to detain tens of thousands of migrants each year and dump them in remote areas, often barren deserts.The full story is here:European funds have been used to train personnel and buy equipment for units implicated in desert dumps and human rights abuses, records and interviews show. Migrants have been pushed back into the most inhospitable parts of North Africa, exposing them to abandonment with no food or water, kidnapping, extortion, sale as human chattel, torture, sexual violence and, in the worst instances, death.
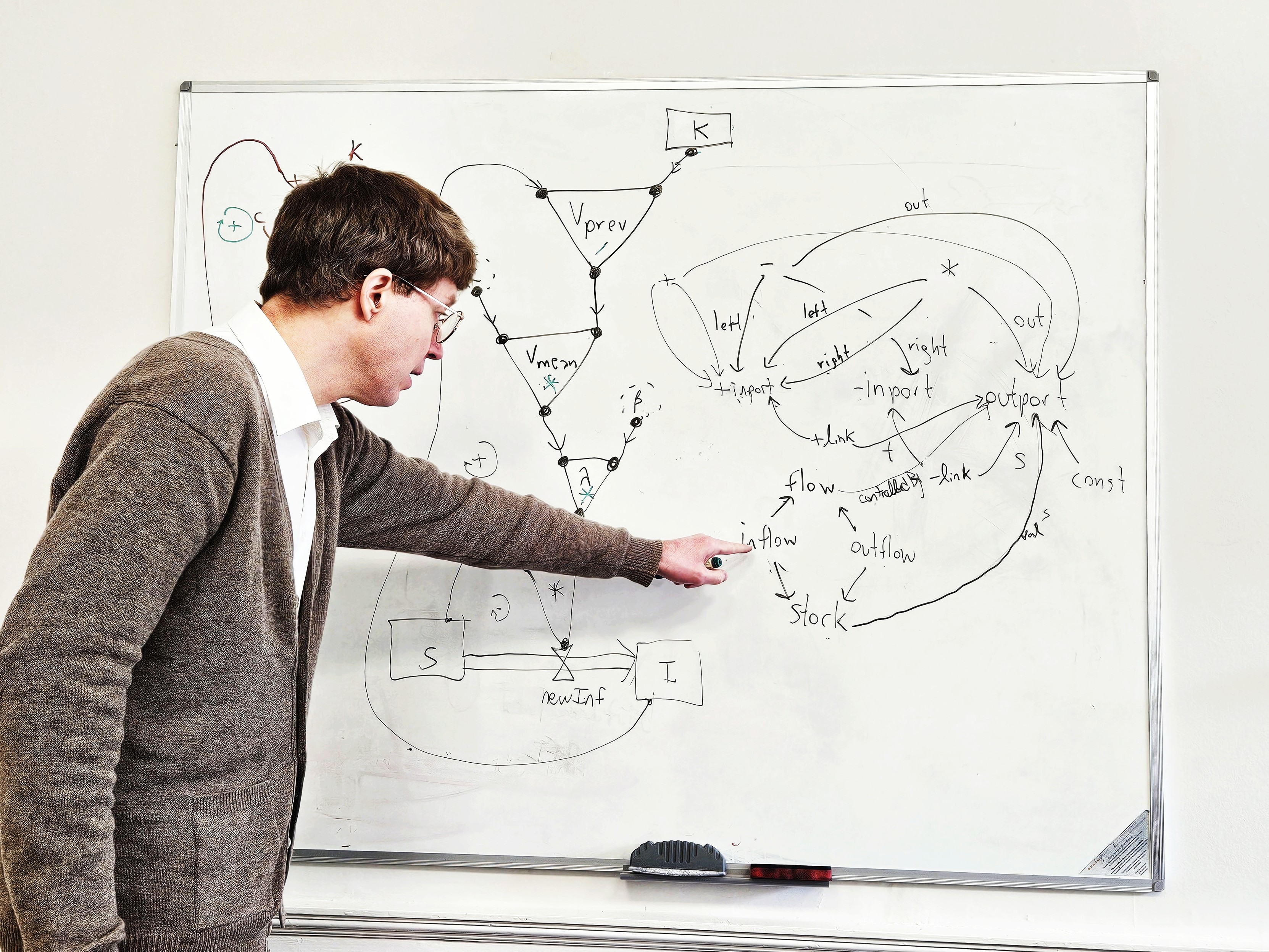
Since May 1st I've been working in Edinburgh with Nate Osgood, Xiaoyan Li, Kris Brown, Evan Patterson and William Waites on a project to build software for agent-based models using category theory. Here is Nate discovering how the process of converting stock and flow diagrams into causal loop diagrams can be captured by a left pushforward functor between presheaf categories. These two kinds of diagrams are both important in the modeling tradition called 'system dynamics', which is used in epidemiology as well as economics and other disciplines.
For more, read:
In the real world, the rope in a knot has some nonzero thickness. In math, knots are made of infinitely thin stuff. This allows mathematical knots to be tied in infinitely complicated ways — ways that are impossible for knots with nonzero thickness! These are called 'wild' knots.
Check out the wild knot in this video by Henry Segerman:
There's just one point where it needs to have zero thickness. So we say it's wild at just one point. But some knots are wild at many points.
There are even knots that are wild at every point! To build these you need to recursively put in wildness at more and more places, forever. I would like to see a good picture of such an everywhere wild knot. I haven't seen one.
Wild knots are extremely hard to classify. This is not just a feeling — it's a theorem. Vadim Kulikov showed that wild knots are harder to classify than any sort of countable structure that you can describe using first-order classical logic with just countably many symbols!
Very roughly speaking, this means wild knots are so complicated that we can't classify them using anything we can write down. This makes them very different from 'tame' knots: knots that aren't wild. Yeah, tame knots are hard to classify, but nowhere near that hard.
Let me say a bit more about this paper:
So he used logic to prove a topology problem is hard — but he also used topology to study logic!
More precisely:
Kulikov studied the topological space of all knots, which are topological embeddings \(K \) of the circle in the 3-sphere. He also studied the equivalence relation on knots saying \(K \sim K' \) if there's a homeomorphism of the 3-sphere mapping \(K \) to \(K' \).
This is an example of a 'Borel relation on a Polish space'. A Polish space is a topological space \(X \) homeomorphic to a complete separable metric space. A Borel relation is a relation \(R \subseteq X \times X \) that's a Borel set. For more about these definitions, click the links.
A lot of classification problems can be thought of this way: you give a Polish space of things you're trying to classify and an equivalence relation saying when two count as 'the same', which is a Borel relation. We then say a Borel relation \(R \subseteq X \times X \) is reducible to a Borel relation \(S \subseteq Y \times Y \) if there's a Borel function \(f: X \to Y \) such that
In this situation people say the classification problem \((X,R) \) can be Borel reduced to the classification problem \((Y,S) \).
This is what Kulikov used to state and prove his result. As far as I can tell, he showed:
1) Equivalence of countable models of any first-order theory with countably many symbols can be Borel reduced to equivalence of (possibly wild) knots.
2) Equivalence of knots is not Borel reducible to the equivalence of countable models of any first-order theory with countably many symbols.
At this point you start noticing that the word 'logical' is hiding inside the word 'topological'.
It's interesting to see how Kulikov proved his result — his paper is so well-written that you can follow the overall logic without sinking into the weeds of detail.
H. Friedman and L. Stanley showed that the space of countable models of any first-order theory with countably many symbols is Borel reducible to a single one of these, coming from the theory of linear orders.
This is pretty surprising to me: I wouldn't have guessed that classifying countable linear orders was maximally difficult in this sense.
But thanks to this, to prove 1) Kulikov just needs to show:
1') Equivalence of countable linear orders can be Borel reduced to equivalence of (possibly wild) knots.
For 2), he uses a general result due to Hjorth. Suppose that a Polish group \(G \) (a group in the category of Polish spaces) acts on a Polish space \(X \) in a 'turbulent' way — some sort of highly chaotic way, defined in Kulikov's paper. Then the Borel relation
$$ x \sim x' \iff \exists g \in G \; g x = x' $$
is not Borel reducible to equivalence of countable models of any first-order theory with countably many symbols!
So Kulikov just needs to show
2') The group of homeomorphisms of the 3-sphere acts in a turbulent way on the space of topological embeddings of the circle in the 3-sphere.
For example, what do categorical logicians think about the problem of classifying countable linear orders? Is there a sense, similar to the one sketched above, in which it's maximally hard among some class of problems? Or does dropping the axiom of choice dramatically change its status?
Also: what do they think about the topology of the space \(X \) of countable models of a first-order theory (which Kulikov says is homeomorphic to the Cantor set)?
I imagine \(X \) is the space of objects of a topological groupoid, where the isomorphisms are the usual isomorphisms of models. But Kulikov merely equips \(X \) with the relation of being isomorphic. That's how the makes it into a Polish space with a Borel equivalence relation.
Similarly, since we have the Polish group of homeomorphisms of \(S^3 \) acting on the Polish space of embeddings \(K : S^1 \to S^3 \), the action groupoid of this groupoid should be a 'Polish groupoid'. But Kulikov instead treats it as a Polish space with a Borel equivalence relation.
May 28, 2024

Using his periodic table, Mendeleev predicted the properties of many elements that hadn't been discovered yet. But he missed others — and more than half of his predicted elements were never found!
Two of the most interesting are coronium and newtonium. He predicted both to have atomic masses lighter than hydrogen!
Mysterious green spectal lines had been seen in the Sun's corona in 1869. Mendeleev was not the only one who thought it was a new element: coronium. He estimated its atomic mass as 0.4. It later turned out to be a highly ionized form of iron, Fe13+, meaning that 13 electrons get knocked off by the extremely high temperatures.
Even more interesting is newtonium. Back then, a lot of people thought light consisted of vibrations in a mysterious substance called the aether. In 1904, in a 50-page paper called “An attempt towards the chemical conception of the aether”, Mendeleev hypothesized that the aether was a noble gas! A bunch of new noble gases had just been discovered, forcing a new column in his table. He dubbed this one newtonium, and he estimated its atomic mass as 0.17.
For Mendeleev's other never-found elements, and how he estimated the masses of coronium and newtonium, read this:
Given how the Catholic Church pressured Galileo to give up his belief that the Earth goes around the Sun, and the Inquisition held him in house arrest for the last 9 years of his life, it's somehow fitting that now his middle finger is a relic.
I'm not kidding, there's even a Wikipedia article just about this: