
...the face appeared to him to be a little changed. The expression looked different. One would have said that there was a touch of cruelty in the mouth. It was certainly strange. — Oscar WildeSadly, I haven't read this story yet — I've just seen a movie version. And I've read some quotes. Since Wilde was a master of the epigram, you can enjoy these like popping down peanuts until you get sick to your stomach:
Nowadays people know the price of everything and the value of nothing.... and so on. You can like them without agreeing with them. If you agreed with them all, Wilde would probably be disappointed.He was always late on principle, his principle being that punctuality is the thief of time.
I never talk during music — at least, during good music. If one hears bad music, it is one's duty to drown it in conversation.
The basis of optimism is sheer terror.
The only way to get rid of temptation is to yield to it. Resist it, and your soul grows sick with longing for the things it has forbidden to itself.
Some people cause happiness wherever they go. Some people cause happiness whenever they go.
The picture here is by an artist named Gerwell.
October 2, 2014
Here's a picture of the hyperbolic plane tiled with apeirogons: polygons with infinitely many sides!
Regular polygons with infinitely many sides are one of those things that make hyperbolic geometry more fun than ordinary Euclidean geometry.
'Apeiro-' is a Greek prefix meaning 'infinite' or 'unlimited'. You know the word 'perimeter', meaning boundary or limit? Well, 'apeiro-' means having no limit. Greek mathematicians were pretty nervous about the infinite, because they thought its unlimitedness made it inherently vague, even chaotic.
The apeirogons are white, and there are 3 meeting at each corner.
In blue we see the dual tiling: there's one blue vertex in the middle of each white polygon, and one blue edge crossing each white edge, and one blue polygon containing each white vertex.
Here are two fun puzzles:
Puzzle 1: What would a regular apeirogon look like in Euclidean geometry?
Puzzle 2: Can you tile the Euclidean plane with regular apeirogons?
And here are two puzzles that are easy if you know what the Schläfli symbol of a tiling is, impossible otherwise:
Puzzle 3: what's the Schläfli symbol of the white tiling?
Puzzle 4: what's the Schläfli symbol of the blue tiling?
This picture was drawn by Don Hatch, but I'm afraid peeking at his page may give away the answer to some of the puzzles!
For some answers, see my G+ post.
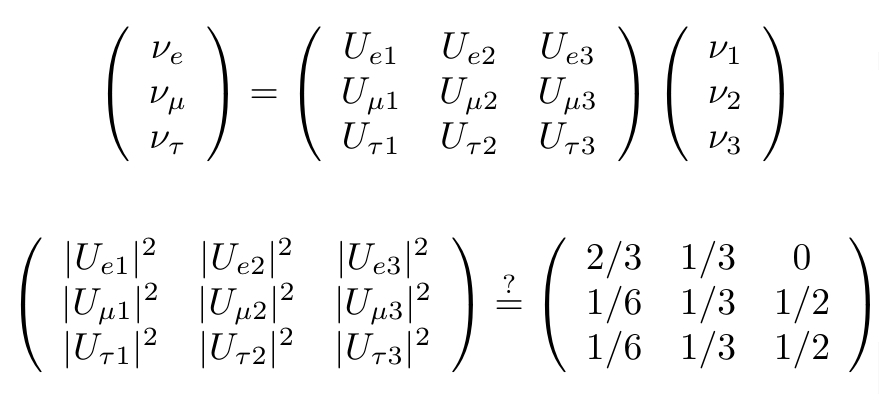
Neutrinos come in 3 kinds, but the 3 kinds with definite masses are not the same as the 3 kinds with definite flavors. They're related by a 3×3 matrix.
Every particle is also a wave, and a particle at rest is a standing wave: it wiggles without going anywhere, like a vibrating piano string. The mass, or more precisely the 'rest mass', of a particle is simply the frequency at which this standing wave vibrates.
But sometimes a particle at rest can wiggle in several different ways with different frequencies. A neutrino can wiggle in 3 ways, and these are called its 'mass eigenstates'. They have boring names: 1, 2 and 3.
The 'flavor' of a neutrino says how it interacts with other particles via the weak force. The flavors have cool names: e (electron), μ (muon), and τ (tau particle).
But a neutrino with a definite flavor does not have a definite mass! A neutrino with a definite flavor is a superposition, or linear combination, of mass eigenstates. The first equation here says how that works. You can understand this if you know about matrix multiplication. We use a 3×3 matrix, the 'neutrino mixing matrix', to write the neutrinos with definite flavor as linear combinations of the mass eigenstates.
What are the numbers in this matrix? Experimentalists have worked very hard over the last few decades trying to measure them. We know some better than others.
They are complex numbers, but there's an interesting guess about their absolute values, shown in the second equation. This guess is called the 'tribimaximal matrix'.
That's a goofy-sounding name! Where did it come from?
With this matrix, the 2nd column is all 1/3's. This means that the 2nd mass eigenstate consists of equal parts of e, μ and τ, so we say it's trimaximally mixed. The 3rd column has two 1/2's. This means that the 3rd mass eigenstate consists of equal parts of μ and τ, so we say it's bimaximally mixed.
Is the tribimaximal matrix right? It is consistent with all known experiments...
... or at least it was until 2012, when this paper seems to have ruled it out:
Great title, eh?
I'm still hoping this experiment made a mistake. If the tribimaximal matrix is wrong, neutrinos remain profoundly mysterious: they're described by a bunch of numbers and we have no idea why these numbers are what they are - since we don't even know exactly what they are.
I wish I knew more about this stuff. For more, try:
By the way, the neutrino mixing matrix is 'unitary': its inverse is the complex conjugate of its transpose. So, the rows say how flavors are superpositions of mass eigenstates — and the columns say how mass eigenstates are superpositions of flavors! I used this when I explained the tribimaximal idea.
Also, because this matrix is unitary, when you take the absolute value
squared of the entries, you get a matrix of nonnegative numbers where
each row sums to 1 and each column sums to 1. So, as soon as we
decide it looks like this:
$$ \left(\begin{array}{ccc}
? & 1/3 & ? \\
? & 1/3 & 1/2 \\
? & 1/3 & 1/2
\end{array}\right)
$$
we know what it must be:
$$ \left( \begin{array}{ccc}
2/3 & 1/3 & 0 \\
1/6 & 1/3 & 1/2 \\
1/6 & 1/3 & 1/2
\end{array} \right)
$$
October 9, 2014
There have been lots of theories saying the Earth is hollow, but I know only one that could be true.
Edmond Halley, the guy who discovered the famous comet, had a theory where Earth consists of a hollow shell about 800 kilometers thick, two smaller shells nested inside, and a ball in the middle — all separated by atmospheres and rotating at different speeds! It sounds nutty, but Halley was trying to explain the Earth's rather complicated magnetic fields: each of his shells was magnetic.
People sometimes accuse Leonhard Euler, the famous mathematician and physicists, of believing the Earth was hollow. But that's not true. In fact, all Euler did was propose a famous thought experiment:
Puzzle: If you could drill a hole all the way through the Earth, and drop a stone in, what would happen?
With the passage of time, scientists have been learning more about geology, so the remaining people who believe in hollow Earth theories get crazier and crazier. For example, the neo-Nazi Ernst Zündel wrote a book entitled UFOs - Nazi Secret Weapons? claiming that Hitler and his men had boarded submarines at the end of the war, escaped to Argentina, and then established a base for flying saucers in a hole leading to the inside of the Earth at the South Pole. Z|ndel also suggested that the Nazis had originated as a separate race that had come from inside the Earth.
My favorite hollow Earth theories are the ones that say we are actually inside! That's right: all of outer space fits inside an Earth-sized ball, while rocks fill the infinite outside of the universe! Or maybe the outside is outer space too... but we're stuck on the inside.
I'm not sure what this theory is supposed to accomplish, but it's fun to think about. What you think are stars may actually be lights from cities on the other side of the Earth! When the Sun sets.... well, there are different ideas about where it goes. Perhaps it goes into a hole? Or perhaps its light bends in such a way that only half the Earth gets sunlight at any one time.
In fact, if you change enough laws of physics, the inside-out Earth theory becomes hard to refute. It becomes our usual theory of the universe described in 'inside-out coordinates', so it becomes equivalent to our usual ideas — except perhaps for one tiny point which I'll mention later.
There's an Egyptian mathematician Mostafa Abdelkader who actually took this line of thought seriously. According to Martin Gardner, this guy claimed that light rays travel in circular paths, and slow as they approach the center of the spherical star-filled hollow Earth. Everything shrinks and slows down as it gets close to the center, so nothing can ever get there. On the other hand, a drill would get longer as you used it to dig outward into the rock.
This theory gets a bit freaky if you drill all the way through the Earth. At some point your drill tip has to suddenly appear on the opposite side of the Universe!
But if you allow this, there's not much difference between the inside-out Universe and ours. True, it's missing one point compared to our usual Universe — namely, the point right at the center of the Earth! But to make up for this, it has an extra point, namely the 'point at infinity', in the center of this inside-out Universe.
In fact, if we include both these points, the Universe itself becomes a '3-sphere', which has two 'hemispheres', namely the inside and the outside of the Earth. One is solid rock, the other empty space. And in fact Dante describes this cosmology in his Divine Comedy. He was a smart dude.
It's a fun exercise in the philosophy of science to figure out why a theory that makes almost identical predictions to our usual theories is nonetheless considered much worse.
For more on hollow Earth theories, try:
The nice mathematical way to turn space inside out is called 'conformal inversion'. It sends straight lines and circles to straight lines and circles, and it preserves angles. You can read more about it here:
And here's the webpage where I got this marvelous picture:
Here is seems that the 'point at infinity' is contained inside a glowing octahedral Heaven, the Moon is bowl-shaped, the Sun's light bends, and there's a hole in the North Pole, leading... where?
Zündel, by the way, was jailed several times for publishing books like The Hitler We Loved and Why and Did Six Million Really Die?:
A domino can knock over a domino that's one and a half times taller. Here you see a tiny domino 5 millimeters tall starting a chain reaction 13 dominos long... which eventually knocks over a domino about a meter tall.
The amount of energy released by the fall of that last domino is 2 billion times the amount of energy it took to knock over the first one!
And if we could do a chain reaction like this 29 dominos long, the final domino would be the size of the Empire State Building!
Puzzle: If each domino is 1.5 times the height of the one that knocked it over, how much longer does it take to fall?
Answer: We can use dimensional analysis to tackled this question. Assuming the overall geometry is just rescaled as we go to larger and larger dominos, and assuming friction can be neglected, the time of fall only depends on:
Thus, anything with units of time built from \(H\) and \(g\) is some constant times $$ \sqrt{H/g} $$
So, the time it takes for each domino to fall and hit the next grows proportionally to \(\sqrt{H}\). So, if each domino is 1.5 times taller than the previous one, it takes about 1.2 times as long to fall!
The time it takes for a dropped rock to hit the ground also grows as \(\sqrt{H}\), for the same reason..
This paper studies the physics of falling dominoes in detail, taking friction into account:
The animated gif above comes from this video by physicist Stephen Morris:
For bigger dominoes, watch this:

Your cells contain mitochondria, little factories that help convert food into useful chemical energy, using oxygen. These guys were once bacteria in their own right! About 1.5 billion years ago they joined forces with cells that couldn't handle oxygen. Now you need them and they need you.
But they still have their own DNA, separate from the rest of the DNA in your cells. Mitochondria are passed down only from mother to child, via the egg cell. So, your mitochondrial DNA gives information about you, your mother, your grandmother, and so on.
Why does mitochondrial DNA come only from the mother? For starters, an egg cell contains 100,000 to 1,000,000 molecules of mitochondrial DNA, while a sperm has only 100 to 1000. On top of that, most mitochondria in a sperm cell stay in the tail, and sometimes the tail is lost during fertilization. But on top of that, in mammals it seems the egg actively destroys any mitochondria that happen to get in from the sperm.
Puzzle 1: Why?
But in biology everything is complicated. Biologists argue about how likely it is for people to inherit mitochondrial DNA from their father. In a test of 172 sheep, three were found to inherit mitochondrial DNA from their father! But in humans, there is so far just one recorded case of it happening.
Your mitochondrial DNA has just 37 genes. It's made of about 16,600 base pairs: molecules called A, T, C and G, just like your ordinary DNA. The information gets copied to RNA when the genes are used to make proteins, and the T gets copied to U, while the rest stay the same.
The chart above shows the mitochondrion's genetic code. More precisely: each codon, or triple of base pairs U, G, A, and C, is translated into an amino acid. Amino acids, the building blocks of proteins, have fun names like phenylalanine, leucine, isoleucine and so on - but in this chart they're abbreviated to Phe, Leu, Ile, etc.
The mitochondrial genetic code is a bit different than the genetic code used elsewhere in your cells! The differences are marked in red:
The same code is used for mitochondria in all vertebrates, as far as I know. Some invertebrates have slightly different mitochondrial genetic codes.
Puzzle 2: Why is the mitochondrial genetic code different in the above ways?
This is an extremely hard puzzle, and I doubt anyone knows the answer for sure, since it could simply be due to random events that happened billions of years ago. But I bet people have thought about it, and I'd love to know any good ideas they've had.
Here's a clue: when the mitochondrial genetic code differs from the 'usual' one, it tends to be simpler! All the mitochondrial genetic code consists of blocks of 2 or 4 codons that do the same thing. Most of the usual code is this way - but AUA and UGA break that rule.

I'm in Banff, listening to a talk on the origin of life at a workshop on Biological and Bio-Inspired Information Theory. The speaker said something like the above... and I was amazed, again, at how wonderful living organisms are.
I gave a talk on Biodiversity, entropy and thermodynamics, and you can watch a video of it here, but what really blew my mind was this talk:
It wasn't easy for me to follow — you should already know rate-distortion theory and the Bellman equation, and I didn't — but it's great! It's all about how living organisms balance the cost of storing information about the past against the payoff of achieving their desired goals in the future. It's not fluff: it's a detailed mathematical model! And it ends by testing the model on experiments with cats listening to music and rats swimming to land.
Here's a good paper about this stuff:
This puffin looks afraid to come out of its burrow. It's probably perfectly happy. But the lines around its eye make it look like a cartoon of nervousness.
Atlantic puffins spend most of their time at sea — they're good at swimming, using their wings to 'fly' underwater as they search for fish to eat. They come to land each spring to breed in colonies on north Atlantic seacoasts and rocky islands. They live in burrows — I just learned this yesterday! Each pair lays one egg, with the male and female sharing incubation duties for about 40 days. After the chick hatches both parents feed it fish for approximately 45 days. After that the young puffling is ready to leave the nest.
You can see life in a puffin burrow here:
I got my info from this website. And the picture here, taken on Skomer Island off southwestern Wales, was posted to Flickr by someone who goes by the name 'Clear Inner Vision'.