

Imagine a black hole with a black ring. Physicists call such a thing a 'black Saturn'.
Nobody has ever seen one. But we can still study them.
You see, we know the equation that describes black holes. It's called Einstein's equation, the basic formula in Einstein's theory of gravity.
We know this equation has solutions with a round event horizon — a surface that you can't escape if you fall through it. These are black holes. And we've seen plenty of black holes — or at least the hot gas falling into black holes.
Could there be a black ring — an event horizon shaped like a ring? It would need to spin so it wouldn't collapse.
Nobody has ever seen a black ring... and there's a reason why! They're mathematically impossible. There's no solution of Einstein's equation that describes a black ring just sitting there, or just spinning but staying the same shape. Physicists have known this since the 1970's. The options for stationary black-hole-like solutions are very limited. You can have a black hole that just sits there, or you can have one that spins... and it can also have electric charge if you want. That's it.
But suppose we had an extra dimension.
Suppose space were 4-dimensional, instead of 3-dimensional. We can still write down Einstein's equation and try to solve it. You can still get round black holes. But in 2001, two physicists proved that black rings are also possible!
Once you have round black holes and black rings, it's irresistible. You've got to see if you can create a black Saturn! Can you get a black ring to orbit a black hole?
Yes you can! In 2007, Henriette Elvanga and Pau Figueras found black Saturn solutions of Einstein's equations in 4d space. And this opened up lots of other fun questions. Can you get the ring to rotate the opposite way than the black hole is spinning? Can you get a black hole with more than one ring orbiting it? Are black Saturns stable, or unstable? And so on.
You might say this is just a game. Or you might say it's important to understand what's so special about 3-dimensional space. Either way, it's pretty cool.
Puzzle 1: Could a ring of dust be stable if there weren't a planet in the middle? Does having a planet inside help stabilize the ring — and if so, how?
I think The Black Saturns would be a good name for a band... and here's one reason why:
Puzzle 2: Why does the phrase 'black Saturn' make sense in terms of astrology? A hint: Jupiter, or Jove, was supposedly responsible for making people 'jovial', or happy.
Here is the first paper on black rings:
If you carry a flashlight and try to shine light straight out, light emitted at the instant you cross the event horizon will basically stay there! Why? Because to stay on the horizon you must move outwards at the speed of light. As the Red Queen said in Alice in Wonderland:
But there's another imaginary sphere outside the event horizon, called the 'photon sphere'. This is where light can go in circles around the black hole!
This picture by David Madore shows the view from the photon sphere. The black hole occupies exactly half the sky! As he says:
This is the distance at which, for an observer standing still, the black hole occupies precisely one half of the visual field. This is because it is the distance at which photons themselves will orbit the black hole circularly (this orbit is unstable, however).In other words, the horizon is the distance at which photons emitted outward from the black hole are standing still, whereas the photon sphere is the distance at which photons emitted orthogonally from the black hole remain at this constant distance and circle around the black hole in an orbit: but since light rays always appear to be straight, to an observer standing still on the photon sphere, the photon sphere seems like an infinite plane, with the black hole occupying half of space beyond it, and the outside world occupying the other half of space.
Now I should admit, as David does, that it's unstable for light to stay exactly on the horizon, or to orbit the photon sphere in a circle. It's like balancing a pencil on its tip! In reality you can't make things so perfect.
And this is especially true because light is a wave, not a particle - so it doesn't have a precise location, it's always a bit smeared out. So, if you have a beam of light orbiting the photon sphere, it will spread out. Some will fall in, and some will escape outwards. I highly recommend David Madore's page on black holes:
The photon sphere of a nonrotating black hole is one and a half times
as big across as the event horizon. The radius of the event horizon is
called the 'Schwarzschild
radius' and it's
$$ \frac{2Gm}{c^2} $$
where \(m\) is the black hole's mass, \(G\) is Newton's gravitational
constant and \(c\) is the speed of light. The radius of the photon sphere is
$$ \frac{3Gm}{c^2}. $$
September 11, 2016
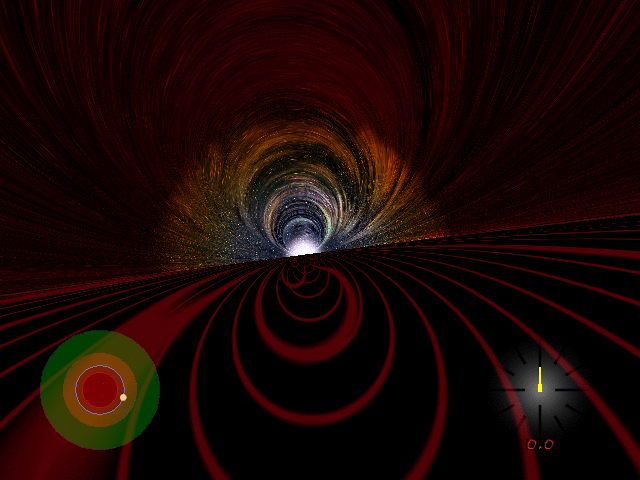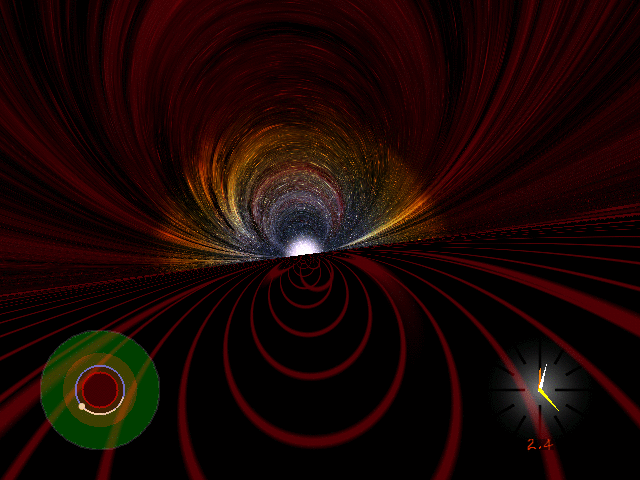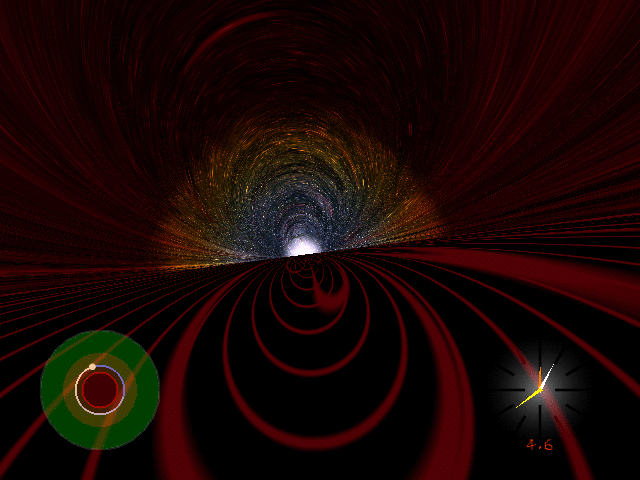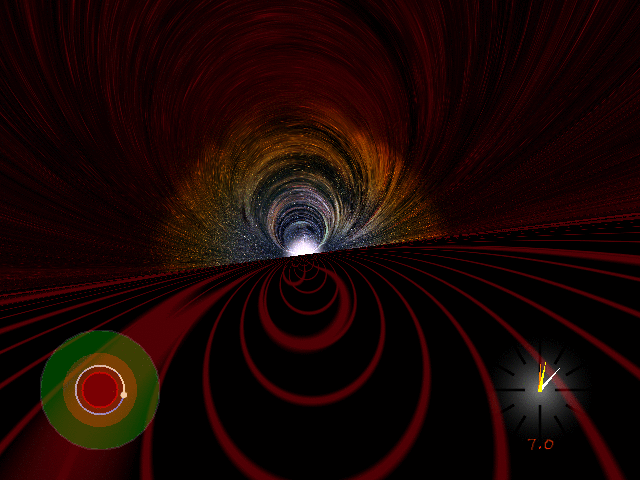
This gif shows what it's like to orbit a non-rotating black hole just above its photon sphere.
That's the imaginary sphere where you'd need to move at the speed of light to maintain a circular orbit. At the photon sphere, the horizon of the black hole looks like a perfectly straight line!
But since you can't move at the speed of light, this gif shows you orbiting slightly above the photon sphere, a bit slower than light.
We cannot go to such a place — not yet, anyway. The gravity would rip us to shreds if we tried. But thanks to physics, we can figure out what it would be like to be there! And that is a wonderful thing.
The red stuff drawn on the black hole is just to help you imagine your motion. You would not really see that stuff.
The light above the black hole is starlight — bent and discolored by your rapid motion and the gravitational field of the black hole.
This gif was made by Andrew Hamilton, an expert on black holes at the University of Colorado. You can see a lot more explanations and movies on his webpage:
This gif by Leo Stein shows a photon orbiting a black hole. Since the black hole is rotating, the photon traces out a complicated path. You can play around with the options here:
If a black hole isn't rotating, light can only orbit it on circles that lie on a special sphere: the photon sphere.
But if the black hole is rotating, photon orbits are more complicated! They always lie on some sphere or other — but now there's a range of spheres of different radii on which photons can move!
The cool part is how a rotating massive object — a black hole, the Sun or even the Earth — warps spacetime in a way that tends to drag objects along with its rotation. This is called 'frame-dragging'.
Frame-dragging was one of the last experimental predictions of general relativity to be verified, using a satellite called Gravity Probe B. Frame-dragging was supposed to make a gyroscope precess a bit more. This experiment was really hard. It suffered massive delays and cost overruns. When it was finally done, the results were not as conclusive as we'd like. I believe in frame-dragging mainly because everything else about general relativity works great, and it's hard to make up a theory that differs in just this one prediction.
It's pretty bizarre that instead of following orbits that move in and out from the black hole — like ellipses, or something similar — photons can move only in orbits of constant radius, with a range of different possible radii being allowed. Leo Stein explains:
After you study the radial equation, you learn that the only bound photon trajectories — that is, orbits! — are those for which \(r = \textrm{constant}\) in Boyer-Lindquist coordinates. This is why these photon orbits are sometimes called 'circular' or 'spherical'.In the end, you see that for each angular momentum parameter \(a\) for the black hole, there is a one-parameter family of trajectories given by the radius \(r\), which must be between the two limits $$ r_1(a) \le r \le r_2(a) $$ The innermost photon orbit is a prograde circle lying in the equatorial plane, and the outermost orbit is a retrograde circle lying in the equatorial plane.
'Prograde' means that the orbit goes around the same way that the black hole is rotating; retrograde means it moves in the opposite direction.
These orbits are all unstable. Push the photon slightly inward and it will fall into the black hole. Push it outward just a bit and it will fly away. So, this stuff is mainly interesting for the math. You won't actually find a lot of light orbiting a black hole.
For more of the math, see Leo Stein's website. It's great! But the most fun part is using some sliders to play with photon orbits. For more on frame-dragging, see:
The 'radial equation' Stein mentions expresses conservation of energy. Usually for an orbiting object in a Newtonian potential this equation takes a form roughly like this: $$ \dot{r}^2 + U(r) = \textrm{constant}$$ where the effective potential \(U\) is concave up with a single minimum, so the radial distance \(r\) oscillates. But in this case \(U\) is concave down with a single maximum, so \(r\) either sits still on top of that maximum or rolls downhill to 0 or infinity.
That's not surprising, since that's what happens already with a photon orbiting a nonrotating black hole. The photon either stays on the photon sphere, or it spirals into the black hole, or it spirals out to infinity.
What's new must be this: the precise form of \(U(r)\) depends on some
angle that says the 'slant' at which the photon crosses the equator
of the rotating black hole. The location of the maximum of \(U(r)\)
depends on this slant angle. So, depending on this slant angle,
we get orbits of different radii.
September 17, 2016

So far all we have is this gif made by Dragana Biocanin. A cat can orbit just above the photon sphere of a non-rotating black hole, moving at almost the speed of light. It's impossible for a cat to orbit below the photon sphere. As long as it's outside the event horizon it can accelerate upwards and escape the black hole's gravitational pull. But if it crosses the event horizon, it's doomed!
The event horizon is an imaginary surface in spacetime that's defined by this property: once a cat crosses this surface, it can't come back without going faster than light! This property involves events in the future, so there's no guaranteed way for the cat to tell when it's crossing an event horizon.
For example, if two supermassive black holes were shooting toward our Solar System right now and collided in an hour, forming a black hole that swallowed the Earth, at some moment your cat would cross the event horizon. That's the moment when, no matter how hard it tried, it could no longer escape. But this moment could be happening right now, and your cat might not notice! No alarm bells ring at this moment.
What happens inside the event horizon?
For a non-rotating black hole formed by the collapse of matter, the answer is pretty well understood — except at the 'singularity', where the laws of physics we know break down.
Your cat will fall in, getting stretched ever thinner. For a hypothetical non-rotating black hole with the mass of our Sun, once it crosses the event horizon it will hit the singularity in about 10 microseconds. That's not much time!
In fact, all known black holes are heavier than our Sun. If you double the mass of the black hole, you double the amount of time it takes to hit the singularity, and so on. So, for a non-rotating black hole 100,000 times the mass of our Sun, it takes 1 second to hit the singularity after crossing the horizon.
The biggest known black holes are about 30 billion times the mass of our Sun. For a non-rotating black hole this big, it would take three and a half days for your cat to hit the singularity after it crosses the horizon! You might want to send it in with some cat food.
But there's a catch. Real-world black holes are always rotating! This makes them much more complicated. For starters, frame-dragging tends to pull you along with the black hole's rotation.
We began to see that in yesterday's diary entry about photons orbit a rotating black hole. There's not just one photon sphere — there's a bunch!
There's also a region called the 'ergosphere' where frame-dragging becomes so strong that your cat can't stand still. And Penrose discovered something interesting about this.
You can send a cat into the ergosphere with rockets strapped to its back. When it shoots back out, it can carry angular momentum and energy out of the black hole! It's a bit like how we use Jupiter to fling satellites to Pluto — except we're using the rotation rather than the motion of the black hole!
So, we can in theory 'mine' a rotating black hole, removing energy from it until it's not rotating.
Beneath the ergosphere lies the horizon. Inside the horizon of a rotating black hole, things get even weirder. More on that later, I hope. But probably not with cats.
For now, try this:
This is a diagram of a Schwarzschild black hole: a non-rotating, uncharged black hole that has been around forever.
Real-world black holes are different. They aren't eternal — they were formed by collapsing matter. They're also rotating. But the Schwarzschild black hole is simple: you can write down a formula for it. So this is the one to start with, when you're studying black holes.
This is a Penrose diagram. It shows time as going up, and just one dimension of space going across. The key to Penrose diagrams is that light moves along diagonal lines. In these diagrams the speed of light is 1. So it moves one inch across for each inch it moves up — that is, forwards in time.
The whole universe outside the black hole is squashed to a diamond. The singularity is the wiggly line at top. The blue curve is the trajectory of a cat falling into the black hole. Since it's moving slower than light, this curve must move more up than across. So, once it crosses the diagonal line called the horizon, it is doomed to hit the singularity.
Indeed, anyone in the region called "Black Hole" will hit the singularity. Notice: when you're in this region, the singularity is not in front of you! It's in your future. Trying to avoid it is like trying to avoid tomorrow.
But what is the diagonal line called the antihorizon? If you start in our universe, there's no way to reach the antihorizon without going faster than light. But we can imagine things crossing it from the other direction: entering from the left and coming in to our universe!
The point is that while this picture of the Schwarzschild black hole is perfectly fine, we can imagine extending it and putting it inside a larger picture. We say it's not maximally extended.
The larger picture, the maximally extended one, describes a very strange world, where things can enter our universe through the antihorizon. But that's another story, which deserves another picture.
If we stick with the diagram here, nothing can come out of the antihorizon, so it will look black. In fact, to anyone in the "Universe" region, it will look like a black sphere. And that's why a Schwarzschild black hole looks like a black sphere from outside!
The weird part is that this black sphere you see, the antihorizon, is different than the sphere you can fall into, namely the horizon.
If this seem confusing, join the club. I think I finally understand it, but nobody ever told me this — at least, not in plain English — so it took me a long time.
What could be behind the antihorizon? If you want to peek, try Andrew Hamilton's page on Penrose diagrams, where I got this picture:
I wish that Wikipedia had a really nice Penrose diagram like this! It's very important. They have some more complicated ones, but the most basic important ones are not drawn very nicely. You need to think about Penrose diagrams to understand black holes and the Big Bang!
Still, their article is worth reading:
For more on the Schwarzschild black hole, read this:
Last time I showed you a Schwarzschild black hole... but not the whole hole.
Besides the horizon, which is the imaginary surface that light can only go in, that picture had a mysterious 'antihorizon', where light can only come out. When you look at this black hole, what you actually see is the antihorizon. The simplest thing is to assume no light is coming out of the antihorizon. Then the black hole will look black.
But I didn't say what was behind the antihorizon!
In a real-world black hole there's no antihorizon, so all this is just for fun. And even in the Schwarzschild black hole, you can never actually cross the antihorizon — unless you can go faster than light. So there's no real need to say what's behind the antihorizon. And we can just decree that no light comes out of it.
But inquiring minds want to know... what could be behind the antihorizon?
This picture shows the answer. This is the maximally extended Schwarzschild black hole — the biggest universe we can imagine, that contains this sort of black hole.
It's really weird.
It contains not only a black hole but also a white hole. The wiggly lines are singularities. Matter and light can only fall into the black hole from our universe... passing through the horizon and hitting the singularity at the top of the picture. And they can only fall out of the white hole into our universe... shooting out of the singularity at the bottom of the picture and passing through the antihorizon.
If that weren't weird enough, there's also a parallel universe, just like ours.
Someone from our universe and someone from the parallel universe can jump into the black hole, meet, say hi, then hit the singularity and die. Fun!
But we can never go from our universe to the parallel universe.
![]()
Why not? Remember, the only allowed paths for people going slower than light are paths that go more up the page than across the page - like the blue path in the picture. To get from our universe to the parallel universe, a path would need to go more across than up.
If you could go faster than light for just a very short time, you could get from our universe to the parallel universe by zipping through the point in the very middle of the picture, where the horizon and antihorizon meet.
Puzzle 1: Suppose the parallel universe has stars in it more or less like ours. You can't see it from our universe — but you could see it if you jumped into the black hole! What would it look like?
Puzzle 2: How would my story change if the "arrow of time" in the parallel universe pointed the other way from ours? In other words, what if the future for them was at the bottom of the picture, rather than the top?
I should emphasize that we're playing games here, but they're games with rules. We're not talking about the real world, but the math of this stuff is well-understood, so you can't just make stuff up. Or you can, but it might be wrong. These puzzles have right and wrong answers!
Unfortunately I haven't really explained things very well, so you may need to guess the answers instead of just figure them out. For more info, try Andrew Hamilton's page, from which I took this picture:
For more on the Schwarzschild black hole, read this:
When you learn general relativity — and when they invent immortality, you'll have time — one of the tricky parts is understanding how a black hole and a white hole combine to give a wormhole.
It's hard to get an intuitive feel for it. But this little movie by Andrew Hamilton helps. A bit.
We're quite sure black holes are real. White holes are purely theoretical. The point is this: if you have a solution of the equation of general relativity, and you 'play the movie backwards', switching the future and the past, you get another solution. And if you do this for a black hole, you get a 'white hole'.
Let's see what a white hole would be like.
In a real-world black hole, matter collapses and forms a singularity, where according to the theory spacetime becomes infinitely curved — but in fact, we don't know what really happens. It would be fun to look at a singularity and find out what it's really like. But unfortunately, the singularity is surrounded by an event horizon. That's an imaginary sphere, where if you enter this sphere you can never get back out. You're doomed to fall into the singularity.
You see, when you cross the event horizon, spacetime is so curved that the singularity is not in front of you. It's in your future — so trying to avoid it is just like trying to avoid next Tuesday!
In summary, viewed from outside: a bunch of ordinary matter collapses into a small region called a black hole. From then on, nothing ever comes out of the black hole: stuff only falls in. (This is ignoring 'Hawking radiation'.)
Now let's play this movie backwards. We start with a small region called a 'white hole'. Nothing ever goes into this white hole: stuff only comes out. Then, eventually, the white hole explodes into a bunch of ordinary matter!
Astronomers have looked for white holes. They've never seen a thing like this. It's not so surprising: the laws of physics say that theoretically, a scrambled egg could be uncooked and stuck back into the shell — and we don't see that either. Some things seem to be more probable than their time-reversed versions.
But all this was just the warmup.
When you take a class in general relativity, they make you find a solution of general relativity that describes a black hole. And the simplest solution doesn't describe a star collapsing and forming a black hole — that's complicated! The simplest solution describes a black hole that has always been there and always will be. That's a lot simpler, because it doesn't change with time: it's perfectly 'static'. You can solve the equations with pencil and paper, not a supercomputer.
But now look! On the one hand, the time-reversed version of this perfectly unchanging thing is again perfectly unchanging. On the other hand, the time-reversed version of a black hole should be a white hole.
So somehow this solution describes both a black hole and a white hole! You can actually chop this solution into two parts, a black hole part and a white hole part. But they fit together.
If we take only the black hole part, we get a picture like this: a black hole that lasts forever. Stuff can fall though the event horizon, and then it's doomed to hit the singularity. Nothing can come out.
If we take only the white hole part, we get a picture like this: a white hole that lasts forever. Stuff can come out of the singularity and come out through the 'reverse event horizon'. But nothing can go into the reverse event horizon.
It's when we we take both parts that things get funny. Now there are two singularities, one in the past and one in the future. But event horizon and the 'reverse event horizon' are the same thing! This horizon is a sphere. Stuff can fall from our universe into this sphere, hit the future singularity and disappear. But stuff can also appear at the past singularity, shoot out of this sphere and enter our universe!
I hope you sort of understood that. It's weird but it's actually logical and symmetrical. You could have guessed it, if you just kept cool and tried to dream up the most symmetrical possibility.
But here's the part you probably couldn't have guessed: this solution also describes two separate universes, connected by a wormhole!
That's the part that freaks me out. Needless to say, this is not something anyone has ever seen. Right now it's just a solution of the equations that describe gravity. But still, I'd like to understand it.
The movie shows how it works. In the little picture at right:
The slice moving up through this little picture shows one way to slice spacetime. That is, it shows the passage of time. The big movie shows that as this happens, the two universes meet and become connected by a wormhole — but then this wormhole snaps and the universes separate!
Unfortunately, you can't actually go from one universe to the other universe. Because you can only go slower than light, once you cross the event horizon you are doomed to hit the future singularity. But before you do, you can meet other doomed people who came from the other universe!
Unfortunately you can never report back and tell people outside the black hole that you met people from another universe... because signals can't get out across the horizon! Bummer.
I should explain this even more, but I'm getting tired, so why don't you just read Andrew Hamilton's description:
By the way, while this gif is a great idea, it's pretty small and a
bit scraggly. I think someone should create a better one and put it
on Wikicommons. This stuff is so cool everyone should have a chance
to learn about it! Even before they invent immortality.
September 26, 2016
As far as we know, all real-world black holes were formed at some moment in time by collapsing matter. But it's easier to find solutions of Einstein's equations that describe an eternal black hole whose shape doesn't change with time.
A rotating eternal black hole is called a Kerr black hole, because this solution of Einstein's equation was first found by Roy Kerr in 1963. However, he just found part of the solution — not the whole picture here!
You see, when you solve Einstein's equations, you get a world obeying the rules of general relativity. But sometimes, if you're not careful, somebody else can find a bigger world that contains yours! It's like you drew a map of the world but you forgot there was anything south of the equator. A solution is called 'maximally extended' if you can't make it any bigger.
This picture shows the maximally extended Kerr solution. It's a Penrose diagram, so moving up the page takes you forward in time, while moving to the right or left edge of the page takes you away from the black hole. Light moves along diagonal lines.
It's a single world, but it has portions called 'Universe', 'Parallel Universe', 'Antiverse', and 'Parallel Antiverse'. Each of these is roughly like our universe, but with no Big Bang. Each lasts forever: time is not drawn to scale.
Each universe, and each parallel universe, has a black hole in it — and also a white hole! Each antiverse, and each parallel antiverse, has a black hole with negative mass, and also a white hole with negative mass.
Only a few of these universes and antiverses are shown here. But there are infinitely many. The pattern repeats forever as you continue to go up or down the picture — that is, forwards or backwards in time.
There's also an infinite repeating sequence of black holes and white holes. And there's more — you can see singularities drawn as wiggly lines. But let's not worry about those yet. There's too much to take in at once.
Let's just follow the blue curve as it goes up the page. This describes a path you could take through space and time.
You could shoot out of a white hole at the very bottom of the picture and wind up in our universe.
Then you could jump into the black hole.
If you dodge the singularities, you could wind up in a new white hole!
And at this point, you have a choice. Swerve right and you go into a new universe. Swerve left and you go into a new parallel universe. They're different — but there's no big difference. In this picture, you choose to enter the new universe.
And so on!
It would be great fun if our universe were part of a grand infinite corridor of universes like this. As far as we know, it's not. I suspect the real universe will be even more amazing. However, we will need much better science and technology to discover what's out there. Right now most of us are stuck here on Earth, and we need to learn to live here. That's a tough challenge too.
My picture is from Andrew Hamilton's wonderful website:
I would like to tell you more about the Kerr black hole — but if I don't get around to it, also check out David Madore's page:

David Madore has a lot of great stuff on his website — videos of black holes, a discussion of infinities, and more. He has an interesting story that claims to tell you the Ultimate Question, and its Answer. (No, it's not 42.) I like it — but how much sense does it make?
Here's the key part:
What is the Ultimate Question, and what is its Answer? The answer to that is, of course: "The Ultimate Question is 'What is the Ultimate Question, and what is its Answer?' and its answer is what has just been given.". This is completely obvious: there is no difference between the question "What color was Alexander's white horse?" and the question "What is the answer to the question 'What color was Alexander's white horse?'?". Consequently, the Ultimate Question is "What is the Answer to the Ultimate Question?" — but so that we can understand the Answer, I restate this as "What is the Ultimate Question, and what is its Answer?", at which point it becomes obvious what the Answer is.Of course it's meant to be funny. I like it. But I wasn't sure how logical it is. The logic is quite twisty — but how much sense does it make? It's more funny if the logic is sound.
Joel David Hamkins and Mike Shulman helped me figure out what was going on, in part by revealing previous work on this puzzle. To learn all about it, read this:
This is the solar wind, the stream of particles coming from the Sun. It was photographed by STEREO. That's the 'Solar Terrestrial Relations Observatory', a pair of satellites we put into orbit around the Sun at the same distance as the Earth, back in 2006. One stays ahead of the Earth, one is behind. Together, they can make stereo movies of the Sun!
One interesting thing is that there's no sharp boundary between the 'outer atmosphere' of the Sun, called the corona, and the solar wind. It's all just hot gas, after all! STEREO has been studying how this gas leaves the corona and forms the solar wind. This picture is a computer-enhanced movie of that process, taken near the Sun's edge.
What's the solar wind made of? When you take hydrogen and helium and heat them up so much that the electrons get knocked off, you get a mix of electrons, hydrogen nuclei (protons), and helium nuclei (made of two protons and two neutrons). So that's all it is.
The Sun's corona is very hot: about a million kelvin. That's hotter than the visible surface of the Sun, called the photosphere! Why does it get so hot? When I last checked, this was still a bit mysterious. But it has something to do with the Sun's powerful magnetic fields.
When they're this hot, some electrons are moving fast enough to break free of the Sun's gravity. Its escape velocity is 600 kilometers per second. The protons and helium nuclei, being heavier but having the same average energy, move slower. So, few of these reach escape velocity.
But with the negatively charged electrons leaving while the positively charged protons and helium nuclei stay behind, this means the corona builds up a positive charge! So the electric field starts to push the protons and helium nuclei away, and some of them — the faster-moving ones — get thrown out too.
Indeed, enough of these positively charged particles have to leave the Sun to balance out the electrons, or the Sun's electric charge would keep getting bigger. It would eventually shoot out huge lightning bolts! The solar wind deals with this problem in a less dramatic way — but sometimes it gets pretty dramatic. Check out this proton storm:
When such storms happen, the US government sends out warnings like this:
Space Weather Message Code: WATA50The solar wind is really complicated, and I've just scratched the surface. I love learning about stuff like this, surfing the web as I lie in bed sipping coffee in the morning. Posting about it just helps organize my thoughts — when you try to explain something, you come up with more questions about it.
Serial Number: 48
Issue Time: 2014 Jan 08 1214 UTC
WATCH: Geomagnetic Storm Category G3 Predicted
Highest Storm Level Predicted by Day:
Jan 08: None (Below G1) Jan 09: G3 (Strong) Jan 10: G3 (Strong)
THIS SUPERSEDES ANY/ALL PRIOR WATCHES IN EFFECT
Potential Impacts: Area of impact primarily poleward of 50 degrees geomagnetic latitude.
Induced Currents — Power system voltage irregularities possible, false alarms may be triggered on some protection devices.
Spacecraft — Systems may experience surface charging; increased drag on low Earth-orbit satellites and orientation problems may occur.
Navigation — Intermittent satellite navigation (GPS) problems, including loss-of-lock and increased range error may occur.
Radio — HF (high frequency) radio may be intermittent.
Aurora — Aurora may be seen as low as Pennsylvania to Iowa to Oregon.
For more on space weather, visit this fun site:
You can see space weather reports here:
Space weather is probably just as complicated as the Earth's weather! For example, there are really at least two kinds of solar wind. According to Wikipedia:
The solar wind is divided into two components, respectively termed the slow solar wind and the fast solar wind. The slow solar wind has a velocity of about 400 km/s, a temperature of 1.4–1.6 × 106 K and a composition that is a close match to the corona. By contrast, the fast solar wind has a typical velocity of 750 km/s, a temperature of 8 × 105 K and it nearly matches the composition of the Sun's photosphere. The slow solar wind is twice as dense and more variable in intensity than the fast solar wind. The slow wind also has a more complex structure, with turbulent regions and large-scale structures.Even when it reaches Earth, the slow solar wind is too hot for hydrogen atoms to form. Around this distance from the Sun, the temperature of protons in the slow solar wind about 40,000 kelvin, while the temperature of the electrons is about 150,000 kelvin. The temperature it takes to for hydrogen atoms to ionize depends on the density, going to zero at zero density, but these temperatures are high enough to keep it ionized it even at densities much higher than that of the solar wind. So, very few atoms will have formed.The slow solar wind appears to originate from a region around the Sun's equatorial belt that is known as the 'streamer belt'. Coronal streamers extend outward from this region, carrying plasma from the interior along closed magnetic loops. Observations of the Sun between 1996 and 2001 showed that emission of the slow solar wind occurred between latitudes of 30-35° around the equator during the solar minimum (the period of lowest solar activity), then expanded toward the poles as the minimum waned. By the time of the solar maximum, the poles were also emitting a slow solar wind.
The fast solar wind is thought to originate from coronal holes, which are funnel-like regions of open field lines in the Sun's magnetic field. Such open lines are particularly prevalent around the Sun's magnetic poles. The plasma source is small magnetic fields created by convection cells in the solar atmosphere. These fields confine the plasma and transport it into the narrow necks of the coronal funnels, which are located only 20,000 kilometers above the photosphere. The plasma is released into the funnel when these magnetic field lines reconnect.
It's interesting that the protons and electrons are so far from equilibrium. That alone proves they haven't bumped into each other enough to equilibriate — much less combine to form atoms.
The story for helium is rather similar, but helium nuclei make up only 4% of the slow solar wind. The fast solar wind is a bit cooler, but not much.
The numbers here are from this article:
For more, read the comments on my G+ post.
For many years I've been wanting to write a paper on 'struggles with the continuum' — that is, the problems in making physical theories mathematically rigorous, due to our assumption that spacetime is a continuum. I offered to contibute such a paper to a book New Spaces in Mathematics and Physics, edited by Mathieu Anel and Gabriel Catren. When the time came to write it, I found myself resisting the duty and procrastinating — in part because it made me feel sad that I'm no longer working on 'fundamental physics' of this sort. But once I got into it, I enjoyed it a lot — except at the end, when I needed to learn more general relativity. This made me ashamed I didn't already know this material better! But when I finally bit the bullet and started work on that part, even that was fun. The paper is more or less done now, except for some small improvements I'd like to make. And I broke it up into a series of short articles which I posted both on my own blog and also Physics Forums: