

I thank Arula
Ratnakar for drawing this picture to accompany my pun.
September 12, 2019

Want a building made from a solid block of stone? Start digging! That's how they built the Church of Saint George in Ethiopia.
But sometimes you can just use a huge rock that happens to be lying around, as they did in Mada'in Saleh, in Arabia:

If we had a time machine, going back just to 4000 BC we could take a tour of ancient lakes of the Sahara... mostly by river, with some portages.
First stop: the Chottis Lake! Second: Lake Ahnet!
Thanks to Carl Churchill for making this. Click on the picture to see
a map that covers more of Africa.
September 13, 2019
Intuitionists don't believe the law of excluded middle, "P or not P".
So they also don't accept proof by contradiction, "not(not P) implies
P".
Do they believe "not(not(P or not P))"?
That is: while these rascals don't believe the law of excluded middle is true, do they at least believe it's not false?
Answer: yes.
In fact, even though they don't believe the law of excluded middle, they believe the negation of the law of excluded middle is false. How can we understand this?
"Are you happy with that?""Well, I'm not unhappy with it."
If we imagine a gap between P and not(P), then it starts seeming quite natural to think intuitionistically. And we can make this precise. Intuitionistic logic is the logic where propositions are open subsets of a topological space. "And" is intersection, "or" is union, but "not" is the interior of the complement. "False" is the empty set and "true" is the whole space.
So in intuitionistic logic, there is often a gap between P and not(P): the "borderline cases". Quite literally: these are the points on the boundary of both the open set P and the interior of its complement!
Since the union of P and the interior of its complement needn't be the whole space, we can't say "P or not(P)" is true. But this union is dense, so taking the interior of its complement gives the empty set. Thus, "not(P or not(P))" is false. And taking the interior of the complement of this gives the whole space. So "not(not(P or not(P)))" is true.
More generally, for any statement of the form not(P), if its negation
is true, not(P) will already be false in intuitionistic logic.
September 14, 2019
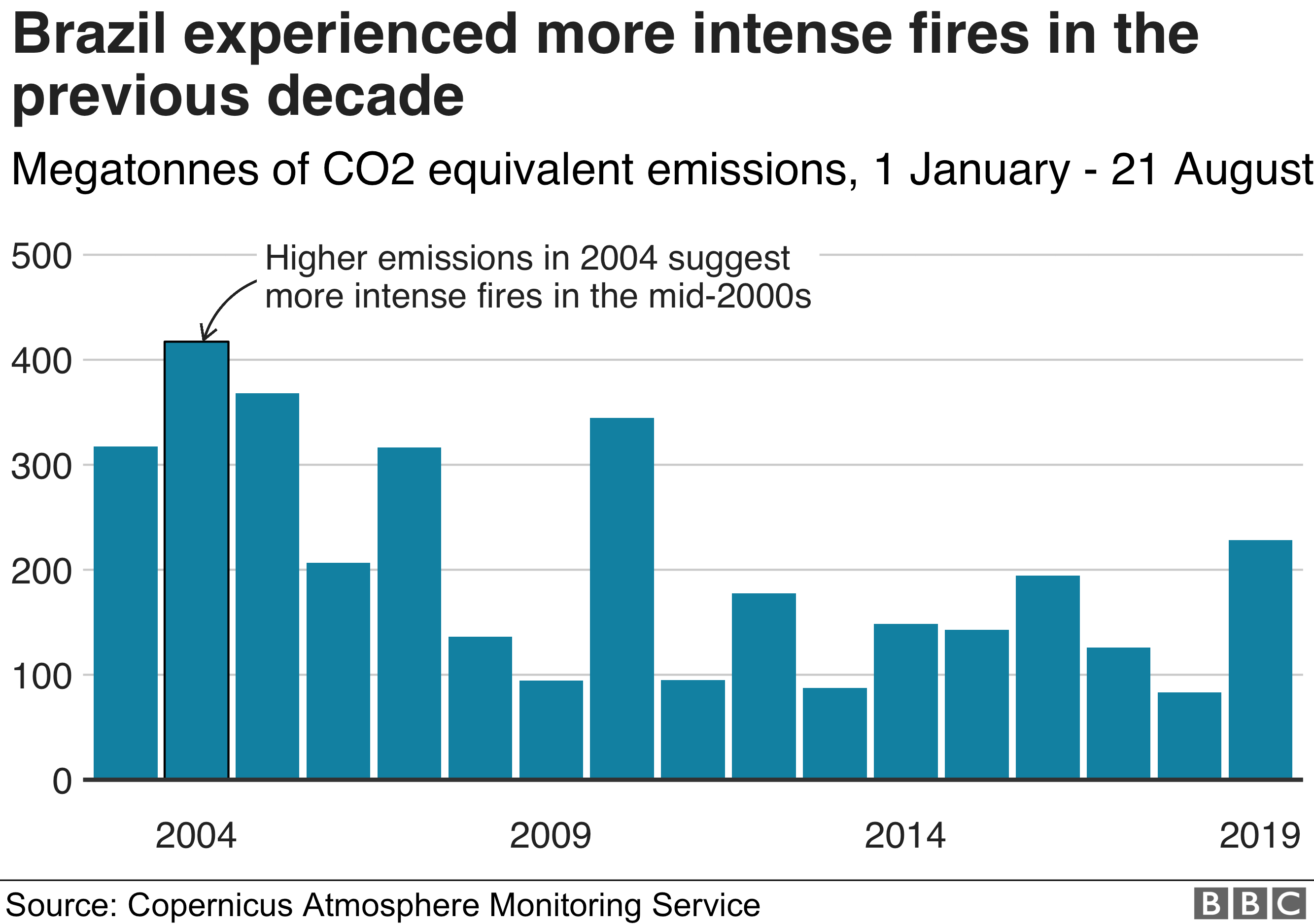
Earlier this summer everyone was upset about the fires in the Amazon. Everyone, it seems, except the president of Brazil. Worrisome though they are, they've been worse before.
Nobody seems to be talking about the fires in Indonesia, which are casting quite a pall here in Singapore. Here's a view from our window today:

This haze isn't nearly as bad as it was in 2015, but it's still unhealthful!
September 15, 2019
Pangolins are
wonderful! Some live here in Singapore. Unfortunately, due to the
idiots who think their scales are medically useful, all eight surviving
species are endangered.
September 26, 2019
Let \(\varphi(n)\) be the number of natural numbers \(\le n\) that
are relatively prime to \(n\). For example, \(\varphi(10) = 4\) since
\(1,3,7\) and \(9\) are relatively prime to \(10\).
Carmichael's Conjecture says that for any \(n\) there exists \(m \ne n\) such that \(\varphi(m) = \varphi(n)\).
The history of this is funny. Robert Carmichael included this as an exercise in his number theory textbook in 1914. But in 1922 he admitted his own proof was wrong. Now it's a famous unsolved problem. This conjecture has been checked in more cases than any other problem in number theory. In 1998, Kevin Ford proved that it's true for $$ n \le 10^{10,000,000,000} $$ But we still don't know if it's true.
Moral: if you can't do the homework, it's not always your fault.
September 27, 2019

If could listen in on any conversations in the past, right now it'd be those between Thelonious Monk and the Baroness Kathleen Annie Pannonica de Koenigswarter, from the Rothschilds — a great supporter of jazz, who even took the rap for Monk when they got caught with some dope.

"Pannonica", or "Nica" as they called her, was a free spirit: an accomplished pilot and huge jazz fan. Her husband the baron divorced her when Charlie Parker died in their home. Later she helped many jazz musician, giving them a place to stay, paying their bills, chauffeuring them to gigs in NYC, even touring with them.

"She realized that jazz needed any kind of help it could get, especially the musicians," said Sonny Rollins. "She was monetarily helpful to a lot who were struggling. But more than that, she was with us. By being with the baroness, we could go places and feel like human beings. It certainly made us feel good. I don’t know how you could measure it. But it was a palpable thing. I think she was a heroic woman."

People used to wonder why she liked Monk so much. Was it sex, drugs, some strange infatuation? How about this: he was one of the coolest cats around. I wish I could hear them talking about music, and life.

Monk stayed at her home after his retirement in 1970, and she helped take care of him through his illness and finally his death in 1982. She died in 1988.
Here is Monk playing his tune "Pannonica":
For more:
Oh, and by the way — she also fought the Nazis as part of the the French resistance in west Africa, serving as a decoder, driver, and radio host. At the end of the war she was decorated with the rank of a lieutenant. For more about her:
Mostly I don't fear death too much. Since age 40 my finite time span is always on my mind. But I just try to do lots of good stuff.
When Lisa had some medical problems a few years ago, I started worrying about "managing the decline" - losing our good health, losing our mental acuity. That will clearly be the biggest challenge to come... sometimes terrifying.
But that's different than death.
Sometimes when I'm on an airplane and it plunges a bit due to turbulence, I get really scared. My body floods with adrenaline and I start sweating. This is some sort of animal reaction to a threat. It seems different from the metaphysical fear of no longer existing.
Some say death is not so bad — the unpleasant part is dying. Woody Allen replied, "I wouldn't mind dying so much if it wasn't that I would be dead at the end of it."
Last year I had a bout of trying to imagine being dead. Silly, I know! But it's too easy to imagine the future continuing as if one were floating above the world, watching it. In reality, it's different. We live a while, and then time ends. This is hard to grasp.
I had a colonoscopy recently — I just got the test results and they're fine. The interesting thing was the sedation. I took off my clothes, put on a hospital gown and lay down on a wheeled stretcher. They poked a needle in my hand and attached me to a tube that would sedate me with a dose of 25–100 micrograms of fentanyl and 1–4 milligrams of midazolam. They rolled me into the operating room. They called out for me to verify my name and give consent, and then...
Lisa was looking down at me, smiling. It was morning and I was in bed. No, I was in a hospital room! As I gathered my wits and starting talking to her, I noticed it was not the operating room. They'd moved me.
It had not been like sleeping. I didn't at all notice myself going unconscious. I didn't dream. There was no passage of time. It was as if someone had surgically removed a chunk of time from my timeline. I'd been compltely gone.
This was what I'd been trying to imagine. With no end.