
Take a bunch of equal-sized balls in 24 dimensions. Take the first ball and get as many others as possible to touch it. The most you can do is 196,560. Continuing on this way, you can pack balls so each touches 196,560 others.
The resulting way of packing balls is unique up to rotations and reflections. It's the densest way to pack balls in 24 dimensions! The balls are centered on a lattice called the 'Leech lattice'.
Now take the group of symmetries of this lattice. The symmetries that preserve the central ball form a group called the 'Conway group' \(\mathrm{Co}_0\). It has 8,315,553,613,086,720,000 elements.
What can we do with this group?
For any group \(G\) there's a space whose fundamental group is this space. There are actually lots, but there's a best one, called the 'classifying space' \(BG\). (It's connected and all its higher homotopy groups vanish.)
The classifying space \(B\mathrm{Co}_0\) of the Conway group should be interesting. How can we study it?
One way is to look at bundles over it. Or 2-bundles, which are bundles of categories. Or 3-bundles, which are bundles of 2-categories!
Theo Johnson-Freyd and David Treumann did roughly this: they classified 3-bundles over \(B\mathrm{Co}_0\) where the fiber is a 2-category with one object, one 1-morphism, and a circle's worth of 2-morphisms.
How many different 3-bundles are there of this sort?
24.
More precisely, they worked out the 4th cohomology of \(B\mathrm{Co}_0\) with integral coefficients, and got \(\mathbb{Z}/24\).
Impressive work... bound to lead to more surprises! Nice title, too.
The Antikythera mechanism, found undersea in the Mediterranean, dates to somewhere between 200 and 60 BC. It's a full-fledged analogue computer! It had at least 30 gears and could predict eclipses, even modelling changes in the Moon's speed as it orbits the Earth.
What Greek knowledge was lost during the Roman takeover? We'll never really know.
They killed Archimedes and plundered Syracuse in 212 BC. Ptolemy the Fat — "Physcon" — put an end to science in Alexandria in 154 BC with brutal persecutions.
Contrary to myth, the Library of Alexandria was not destroyed once and for all in a single huge fire. The sixth head librarian, Aristarchus of Samothrace, fled when Physcon took over. The library was indeed set on fire in the civil war of 48 BC. But it seems to have lasted until 260 AD, when it basically lost its funding.
When the Romans took over, they dumbed things down. In his marvelous book The Forgotten Revolution, quoted below, Lucio Russo explains the evil effects.
Another example: we have the first 4 books by Apollonius on conic sections — the more elementary ones — but the other 3 have been lost.
Archimedes figured out the volume and surface area of a sphere, and the area under a parabola, in a letter to Eratosthenes. He used modern ideas like 'infinitesimals'! The letter was repeatedly copied and made its way into a 10th-century Byzantine parchment manuscript. But this parchment was written over by Christian monks in the 13th century, and only rediscovered in 1906.
There's no way to tell how much has been permanently lost. So we'll never know the full heights of Greek science and mathematics. If we hadn't found one example of an analogue computer in a shipwreck in 1902, we wouldn't have guessed they could make those!
And we shouldn't count on our current knowledge lasting forever, either.
Here are some more things to read. Most of all I recommend this book:
The complex numbers together with infinity form a sphere called the Riemann sphere. The 6 simplest numbers on this sphere lie at the north pole, the south pole, the east pole, the west pole, the front pole and the back pole. They're the corners of an octahedron!
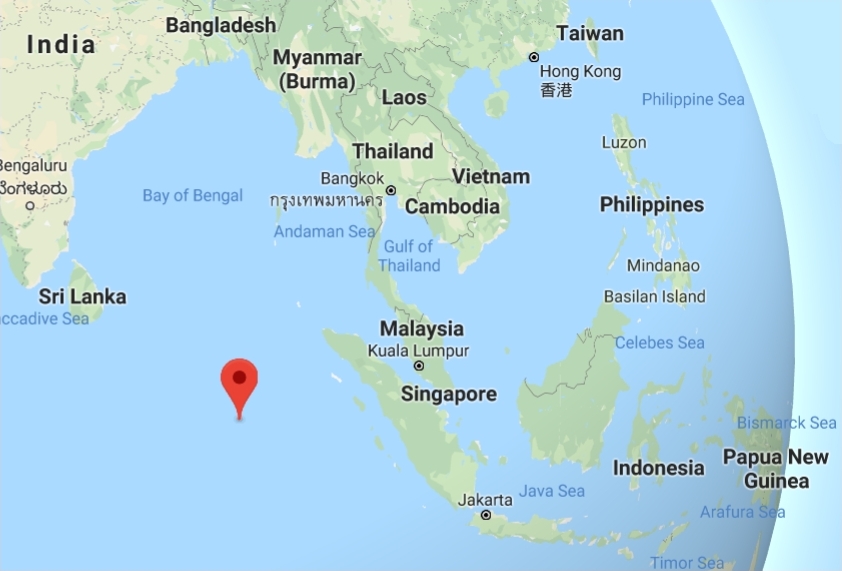
On the Earth, I'd say the "front pole" is where the prime meridian meets the equator at 0°N 0°E. It's called Null Island but there's just a buoy there. Here it is:
Where's the back pole, the east pole and the west pole? I'll leave two of these as puzzles, but I discovered that in Singapore I'm fairly close to the east pole:
If you think of the octahedron's corners as the quaternions \(\pm i, \pm j, \pm k\), you can look for unit quaternions \(q\) such that whenever \(x\) is one of these corners, so is \(qxq^{-1}\). There are 48 of these! They form a group called the binary octahedral group.
By how we set it up, the binary octahedral group acts as rotational symmetries of the octahedron: any transformation sending \(x\) to \(qxq^{-1}\) is a rotation. But this group is a double cover of the octahedron's rotational symmetry group! That is, pairs of elements of the binary octahedral group describe the same rotation of the octahedron.
If we go back and think of the Earth's 6 poles as points \(0, \pm 1, \pm i, \infty\) on the Riemann sphere instead of \(\pm i, \pm j, \pm k\), we can think of the binary octahedral group as a subgroup of \(\mathrm{SL}(2,\mathbb{C}\)), since this acts as conformal transformations of the Riemann sphere!
If we do this, the binary octahedral group is actually a subgroup of \(\mathrm{SU}(2)\), the double cover of the rotation group — which is isomorphic to the group of unit quaternions. So it all hangs together.
It's fun to actualy see the unit quaternions in the binary octahedral group. First we have 8 that form the corners of a cross-polytope (the 4d analogue of an octahedron): $$ \pm 1, \pm i , \pm j , \pm k $$ These form a group on their own, called the quaternion group. Then we have 16 that form the corners of a hypercube (the 4d analogue of a cube, also called a tesseract or 4-cube): $$ \frac{\pm 1 \pm i \pm j \pm k}{2} $$ These don't form a group, but if we take them together with the 8 previous ones we get a 24-element subgroup of the unit quaternions called the binary tetrahedral group. They're also the vertices of a 24-cell, which is yet another highly symmetrical shape in 4 dimensions (one that doesn't have a 3d analogue).
That accounts for half the quaternions in the binary octahedral group! Here are the other 24: $$ \frac{\pm 1 \pm i}{\sqrt{2}}, \frac{\pm 1 \pm j}{\sqrt{2}}, \frac{\pm 1 \pm k}{\sqrt{2}}, $$ $$ \frac{\pm i \pm j}{\sqrt{2}}, \frac{\pm j \pm k}{\sqrt{2}}, \frac{\pm k \pm i}{\sqrt{2}} $$ These form the vertices of another 24-cell!
The first 24 quaternions, those in the binary tetrahedral group, give rotations that preserve each of the two tetrahedra that you can fit around an octahedron like this:
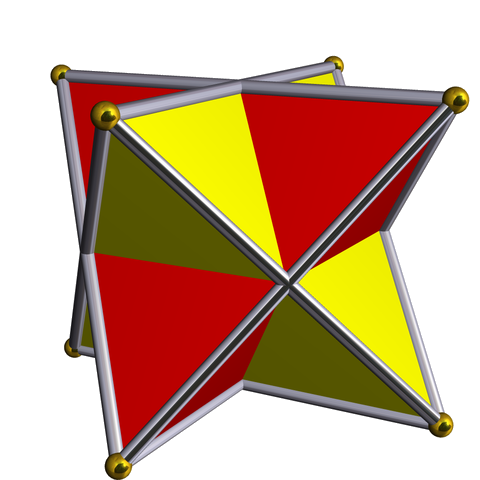
The 6 elements
$$ \pm i , \pm j , \pm k $$
describe 180° rotations around the octahedron's 3 axes, the 16 elements
$$ \frac{\pm 1 \pm i \pm j \pm k}{2} $$
describe 120° clockwise rotations of the octahedron's 8 triangles, the
12 elements
$$ \frac{\pm 1 \pm i}{\sqrt{2}}, \frac{\pm 1 \pm j}{\sqrt{2}}, \frac{\pm 1 \pm k}{\sqrt{2}}, $$
describe 90° clockwise rotations holding fixed one of the octahedron's 6
vertices, and the 12 elements
$$ \frac{\pm i \pm j}{\sqrt{2}}, \frac{\pm j \pm k}{\sqrt{2}}, \frac{\pm k \pm i}{\sqrt{2}} $$
describe 180° clockwise rotations of the octahedron's 6 opposite pairs
of edges.
August 28, 2019
Among finite groups, there are frighteningly many whose number of
elements is a power of 2. For example, there are
$$ 49,910,529,484 $$
nonisomorphic groups with at most 2000 elements. Of these, over 99% have
exactly \(2^{10} = 1024\) elements!
Why are there so many groups whose size is a power of 2? You can think of them as funny ways to add strings of bits.
The simplest way is to add all the bits separately, mod 2, as shown below. It's like addition in base 2 but without any carrying!

But there are lots of other ways to add bit strings that give groups! For example we can carry as usual when adding in base 2... except for the leftmost entry, where we don't bother to carry.

There are groups where we add bit strings and do our carrying in stranger in ways! Below is one of the simpler methods. There are 14 fundamentally different groups with 16 elements. All come from different rules for carrying when we add bit strings!

Here's a cool theorem. Any group whose number of elements is a power of 2 can be gotten from a way of adding bit strings with a weird rule for carrying... where "carrying" only affects the digits to the left of the digits you're adding, but possibly affects more than one of these digits.
Mathematicians usually say this theorem another way: they say "any finite 2-group is nilpotent". A "finite 2-group" is a group whose number of elements is a power of 2. "Nilpotent" means it can be described using bit strings and carrying in the way I just explained (although it takes some work to show this starting from the usual definition).
In fact all this stuff about the number 2 works equally well for any prime number \(p\). Any finite \(p\)-group is nilpotent... but now, instead of bit strings, we need to describe it strings of integers mod \(p\).
Nilpotent groups are an absolute bitch to classify.
Because 2 is the smallest prime, when you classify groups of size \(\lt N\), the power of a prime with the highest possible exponent that's \(\lt N\) will always be a power of 2. This is part of why most finite groups are 2-groups!
It's "the power of two".
For more read: