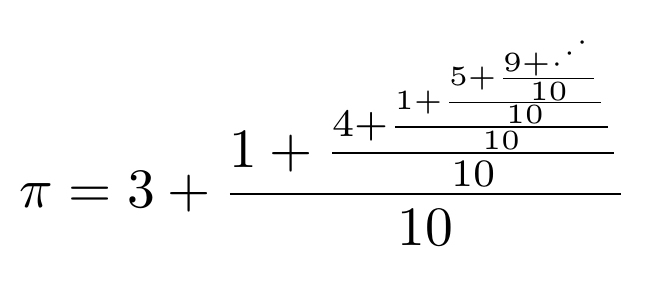
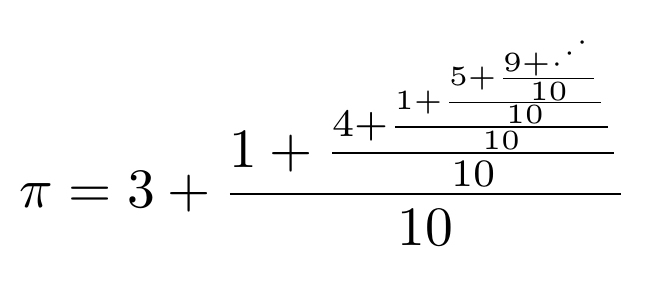
Move over, Ramanujan! I think I'm getting good at this!
September 4, 2020

They started playing this organ piece in 2001, but it began with 17 months of silence. The first actual note started in 2003.
The fifteenth chord will begin tomorrow!
It will last for 639 years.
The last change was on October 5, 2013:
The next will be on February 5, 2022.

I finally figured out the point of Riccati equations. They're the next thing after first-order linear ODE: they're quadratic.
But the real point is that to get the solution \(y(t)\) you just do a fractional linear transformation of the initial value \(y(0)\)!
It's good to compare first-order linear ODE. For these, to get the solution \(y(t)\) at any time, you do an affine transformation of the initial value \(y(0)\). (Some people would call \(y(t) = a(t)y(0) + b(t)\) 'linear', but I'd say 'affine' unless \(b(t) = 0\).)

A fractional linear transformation is really a transformation of the Riemann sphere \(\mathbb{C}\mathrm{P}^1\). A solution of a Riccati equation can become infinite, but if we think of it as taking values in \(\mathbb{C}\mathrm{P}^1\) then that's okay!
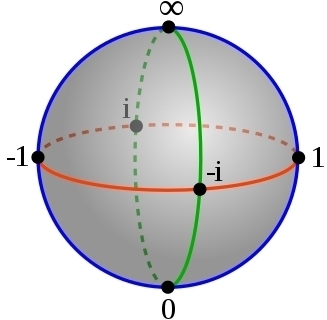
In algebraic geometry \(\mathbb{C}\) is the 'affine line' over the complex numbers, while \(\mathbb{C}\mathrm{P}^1\) is the 'projective line'. So, linear first-order ODE are to Riccati equations as affine geometry is to projective geometry!
The analogy goes quite deep. More here:

Nina Holden just won the 2021 Maryam Mirzakhani New Frontiers Prize for her work on random surfaces and the mathematics of quantum gravity!
I'd like to tell you what she did... but I'm so far behind I'll just explain a bit of the background.
Suppose you randomly choose a triangulation of the sphere with \(n\) triangles. This is a purely combinatorial thing, but you can think of it as a metric space if each of the triangles is equilateral with all sides of length 1. This is a distorted picture of what you might get, drawn by Jérémie Bettinelli:
The triangles are not drawn as equilateral, so we can fit this shape into 3d space. Visit Bettinelli's page for images that you can rotate:
I've described how to build a random space out of \(n\) triangles. In the limit \(n \to \infty\), if you rescale the resulting space by a factor of \(n^{-1/4}\) so it doesn't get bigger and bigger, it converges to a 'random metric space' with fascinating properties.
This random metric space is on average so wrinkly and crinkly that 'almost surely' — that is, with probability 1 — its Hausdorff dimension is not 2 but 4. And yet it is almost surely homeomorphic to a sphere!
Rigorously proving this is hard: a mix of combinatorics, probability theory and geometry.
Ideas from physics are also important here. There's a theory called 'Liouville quantum gravity' that describes these random 2-dimensional surfaces. So, physicists have ways of — nonrigorously — figuring out answers to some questions faster than the mathematicians!
The technical name for the random surface I'm talking about is 'the Brownian map'. A key step in understanding it was this paper from 2013:
The Brownian map is to surfaces what Brownian motion is to curves. The fractal dimension of Brownian motion is almost surely 2: twice the dimension of a smooth curve. For the Brownian map it's almost surely 4: twice the dimension of a smooth surface.
Let me just say one more technical thing. There's a 'space of all compact metric spaces', and the random surface I'm talking about is actually a probability measure on this space! It's called the Gromov-Hausdorff space, and it itself is a metric space... but not compact.
There's a lot more to say about this... but I haven't gotten very close to understanding Nina Holden's work yet. She wrote a 7-paper series leading up to this one:
This is a much easier place to start learning this general subject:

Condensed matter physics is so cool!
You can make materials called 'spin ices' that act like universes where the usual laws of quantum electrodynamics are modified! The speed of light is much lower — and even better, the fine structure constant can be larger.
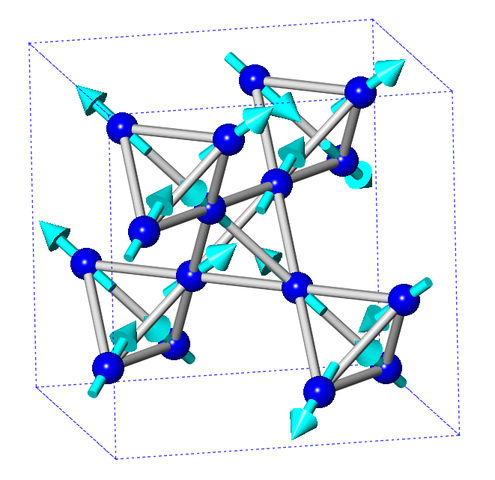
A 'spin ice' is a crystal made of tetrahedra. In the low-energy states, in each tetrahedron two electron spins point out and two point in. So, if you pretend the electron spins are an electric field, the divergence of the electric field is zero. It's just an analogy. But the analogy goes deeper! As time passes, the spins move around in ways that mimic the usual laws of electricity and magnetism — but with a speed of light that's much slower: about 10 meters per second.
'Defects' where the two-in, two-out rule for spins are broken act like charged particles, since the (pretend) electric field points in or out at these places. And since these defects have extra energy, these charged particles have mass.
Unlike our universe, a spin ice also allows for magnetic monopoles, where the magnetic field points in or out. I don't understand how yet. And by adjusting the interactions in your spin ice (called the RK and 3NN potentials), you can change the fine structure constant!
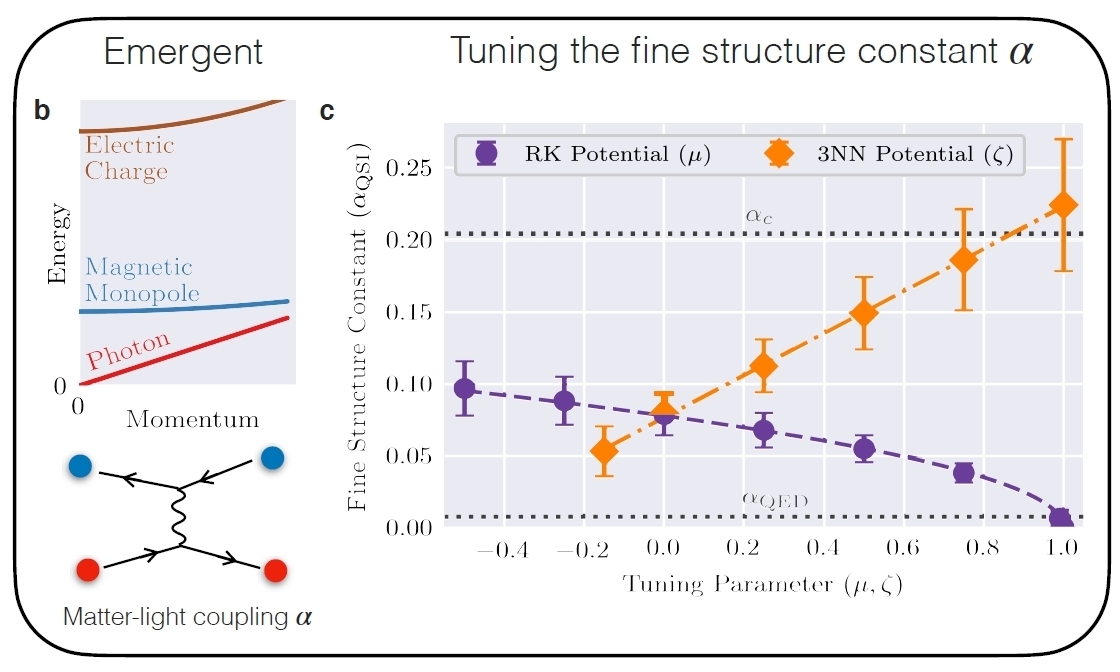
The fine structure constant \(\alpha\) measures the strength of interactions between charged matter and the electromagnetic field. In our universe it's about 1/137. We believe that if it were much larger the electromagnetic field would be 'confined' like the strong force.
So, spin ices offer a playground where people can study physics in worlds with magnetic monopoles - and different choices of fine structure constant. But this work is just beginning! The paper is here:

Some mathematical objects are pushed into the background, not taught in courses at the appropriate moment. As a result, the development of mathematics is deformed.
For example: the humble 'rig' or 'ring without negatives'. Any decent modern algebra course will talk about rings. Few dare mention rigs! As a result, these important mathematical objects are left in the cold:
Instead of proving theorems about monoids, a typical course in algebra goes straight to groups. Thus the free group on one generator, the group of integers \(\mathbb{Z}\), reigns supreme — while the free monoid on one generator, \(\mathbb{N}\), is treated like dirt.
Since groups are enthroned while monoids are shunned, every algebra class talks about kernels and normal subgroups — but few discuss equalizers and congruence relations, which are more general, more fundamental, and ultimately simpler.
Then, when they throw multiplication into the mix, our courses talk about rings, which are monoids in \((\mathrm{AbGp}, \otimes)\), but not rigs, which are monoids in \((\mathrm{CommMon}, \otimes)\). Indeed, it's strangely hard to find a good intro to the tensor product of commutative monoids!
In algebra class we all learn about modules of rings, and discover to our delight that abelian groups are a special case: namely, \(\mathbb{Z}\)-modules. Few of us learn about modules of rigs, or learn that commutative monoids are \(\mathbb{N}\)-modules.
They teach us about the ring of matrices with entries in a ring... but not the rig of matrices with entries in a rig! Thus, only an elite few learn that relations are matrices with entries in the boolean rig \(\mathbb{B} = \{F,T\}\), with matrix operations having important meanings.
I think the exclusion of the booleans from algebra class helps hide the beautiful connections between algebra and logic. And the exclusion of both booleans and natural numbers must make computer scientists feel abstract algebra is "not for us".
Someday monoids and rigs will become part of a typical algebra class. Don't get me wrong: I love groups and rings. But the beautiful structure of mathematics is hidden if we neglect the wonderful world without negatives.