
NASA put out a fun series of posters called Galaxy of Horrors. Here are some of my favorites.
Take a tour of some of the most terrifying and mind-blowing destinations in our galaxy ... and beyond. After a visit to these nightmare worlds, you may never want to leave Earth again! You can also download our free posters — based on real NASA science — if you dare.
This bone-chilling force will leave you shivering alone in terror!An unseen power is prowling throughout the cosmos, driving the universe to expand at a quickening rate. This relentless pressure, called DARK ENERGY, is nothing like dark matter, that mysterious material only revealed by its gravitational pull. Dark energy offers a bigger fright: pushing galaxies farther apart over trillions of years, leaving the universe to an inescapable, freezing death in the pitch black expanse of outer space.
Something strange and mysterious creeps throughout the cosmos. Scientists call it DARK MATTER. It is scattered in an intricate web that forms the skeleton of our universe. Dark matter is invisible, only revealing its presence by pushing and pulling on objects we can see.
In the depths of the universe, the cores of two collapsed stars violently merge to release a burst of the deadliest and most powerful form of light, known as gamma rays. These beams of doom are unleashed upon their unfortunate surroundings, shining a million trillion times brighter than the Sun for up to 30 terrifying seconds. Nothing can shield you from the blinding destruction of the gamma ray ghouls!

Shimmering in the night of space, a solar sail is pushed by the pressure of photons from the sun as it orbits the earth. It's just a test — for now it's tumbling, its engines not yet keeping it aligned. But it's another step toward the dream of solar-powered space flight.
This photo is taken from the solar sail itself. It has four black-and-white wide-angle cameras, centrally located aboard the spacecraft. Near the bottom of the photo, the view from one camera shows the reflective sail quadrants supported by booms. At the top of the photo is the back of one of the sail's solar panels. The booms are mounted at right angles, and the solar panel is rectangular, but they're distorted by the wide-angle camera.
The sail is called the Advanced Composite Solar Sail System. Here's an artist's prettier picture of what it might look like from afar:

A company called Rocket Lab launched the Advanced Composite Solar Sail System for NASA on April 23, 2024. It went 1000 kilometers up — high enough for the tiny force of sunlight on the sails to overcome atmospheric drag and help the craft gain altitude. Last week the sails came out. Now the craft is flying without attitude control, slowly tumbling. Once the mission team finishes testing the booms and sail, they'll turn on the spacecraft’s attitude control system. This will stabilize the spacecraft and stop the tumbling. Eventually they will start maneuvers that should raise and lower the spacecraft’s orbit — sailing in sunlight, pushed by the gentle pressure of photons!
You can read the Advanced Composite Solar Sail System blog here:
What's the next step? I don't really know. I asked around, and Isaac Kuo said:
I'm not sure what's next. NEA Scout failed; unclear what went wrong.Of course, IKAROS famously succeeded, but it has not led to further solar sail missions using its type of solution.
It doesn't seem ready for prime time — not a serious alternative to solar electric propulsion for, say, multiple asteroid missions (like Dawn).
A physical framework often depends on some physical constants that we can imagine varying, and in some limit one framework may reduce to another. This suggests that we should study a 'moduli space' or 'moduli stack' of physical frameworks. To do this formally, in full generality, we'd need to define what counts as a 'framework', and what means for two frameworks to be equivalent. I'm not ready to try that yet. So instead, I want to study an example: a 1-parameter family of physical frameworks that includes classical statistical mechanics — and, I hope, also thermodynamics!
Physicists often say things like this:
"Special relativity reduces to Newtonian mechanics as the speed of light, \(c\), approaches \(\infty\)."
"Quantum mechanics reduces to classical mechanics as Planck's constant \(\hbar\) approaches \(0\)."
"General relativity reduces to special relativity as Newton's constant \(G\) approaches \(0\)."
Sometimes they try to elaborate this further with a picture called Bronstein's cube or the CGh cube:
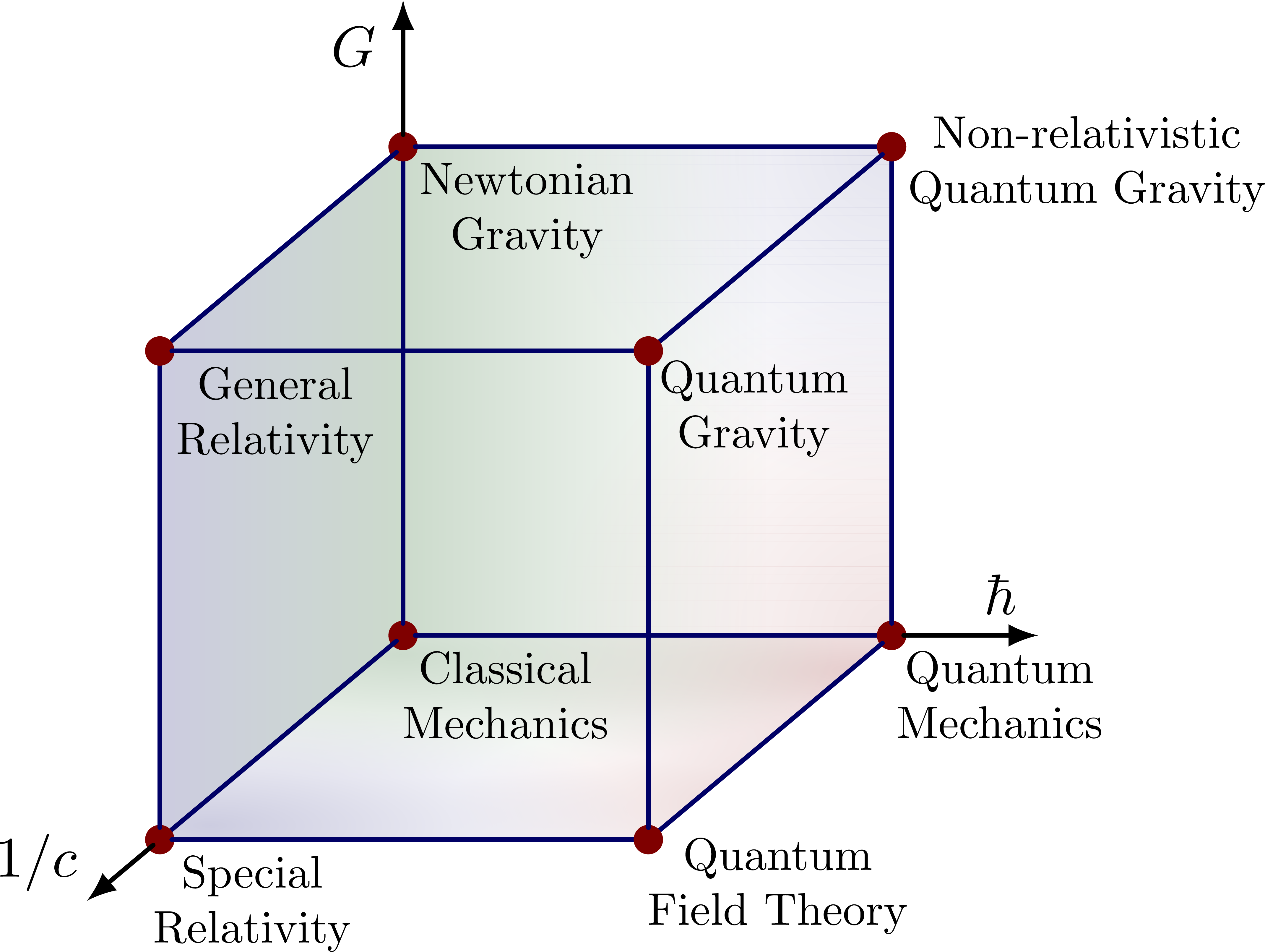
This is presumably hinting at some 3-dimensional space where \(1/c, \hbar\) and \(G\) can take arbitrary nonnegative values. This would be an example of what I mean by a 'moduli space of physical frameworks'.
But right now I want to talk about talk about a fourth dimension that's not in this cube. I want to talk about whether classical statistical mechanics reduces to classical thermodynamics as \(k \to 0\), where \(k\) is Boltzmann's constant.
Since thermodynamics and statistical mechanics are often taught in the same course, you may be wondering how I distinguish them. Here are my two key principles: anything that involves probability theory or Boltzmann's constant I will not call thermodynamics: I will call it statistical mechanics. For example, in thermodynamics we have quantities like energy \(E\), entropy \(S\), temperature \(T\), obeying rules like $$ d E = T d S $$ But in classical statistical mechanics \(E\) becomes a random variable and we instead have $$ d \langle E \rangle = T d S $$ In classical statistical mechanics we can also compute the variance of \(E\), and this is typically proportional to Boltzmann's constant. As \(k \to 0\) this variance goes to zero and we're back to thermodynamics! Also, in classical statistical mechanics entropy turns out to be given by $$ S = - k \int_X p(x) \ln(p(x)) \, d\mu(x) $$ where \(p\) is some probability distribution on some measure space of states \((X,\mu)\).
I want to flesh out how classical statistical mechanics reduces to thermodynamics as \(k \to 0\), and my hope is that this is quite analogous to how quantum mechanics reduces to classical mechanics as \(\hbar \to 0\):
| taking the \(\hbar \to 0\) limit of | taking the \(k \to 0\) limit of |
| Quantum Mechanics | Classical Statistical Mechanics |
| gives | gives |
| Classical Mechanics | Thermodynamics |
Here's the idea. Quantum fluctuations are a form of randomness inherent to quantum mechanics, described by complex amplitudes. Thermal fluctuations are a form of randomness inherent to classical statistical mechanics, described by real probabilities. Planck's constant \(\hbar\) sets the scale of quantum fluctuations, and as \(\hbar \to 0\) these go away and quantum mechanics reduces to classical mechanics. Boltzmann's constant \(k\) sets the scale of thermal fluctuations, and as \(k \to 0\) these go away and classical statistical mechanics reduces to thermodynamics.
If this idea works, the whole story for how quantum mechanics reduces to classical mechanics as \(\hbar \to 0\) may be a Wick rotated version of how classical statistical mechanics reduces to thermodynamics as \(k \to 0\). In other words, the two stories may be formally the same if we replace \(k\) everywhere with \(i \hbar\).
However, there are many obstacles to getting the idea to to work — or at least apparent obstacles, much as walls can feel like 'obstacles' when you're trying to walk through a wide open door at night. Even before we meet the technical problems with Wick rotation, there's the preliminary problem of getting thermodynamics to actually arise as the \(k \to 0\) limit of classical statistical mechanics!
So despite the grand words above, it's that preliminary problem that I'm focused on now. It's actually really interesting.
Today I'll just give a bit of background.
Idempotent analysis overlaps with 'tropical mathematics', where people use this number system, called the 'tropical rig', to simplify problems in algebraic geometry. People who do idempotent analysis are motivated more by applications to physics:
The basic idea is to study a 1-parameter family of rigs \(R_\beta\) which for finite \(\beta \gt 0\) are all isomorphic to \((-\infty,\infty]\) with its usual addition and multiplication, but in the limit \(\beta \to +\infty\) approach a rig isomorphic to \([0,\infty)\) with 'min' as addition and the usual \(+\) as multiplication.
Let me describe this in more detail, so you can see exactly how it works. In classical statistical mechanics, the probability of a system being in a state of energy \(E\) decreases exponentially with energy, so it's proportional to $$ e^{-\beta E} $$ where \(\beta \gt 0\) is some constant we'll discuss later. Let's write $$ f_\beta(E) = e^{-\beta E} $$ but let's extend \(f_\beta\) to a bijection $$f_\beta: (-\infty, \infty] \to [0,\infty) $$ sending \(\infty\) to \(0\). This says that states of infinite energy have probability zero. Now let's conjugate ordinary addition and multiplication, which make \([0,\infty)\) into a rig, by this bijection \(f_\beta\): $$ x \oplus_\beta y = f_\beta^{-1} (f_\beta(x) + f_\beta(y)) $$
$$ x \odot_\beta y = f_\beta^{-1} (f_\beta(x) \cdot f_\beta(y)) $$ These conjugated operations make \((-\infty,\infty]\) into a rig. Explicitly, we have $$ x \oplus_\beta y = -\frac{1}{\beta} \ln(e^{-\beta x} + e^{-\beta y}) $$
$$ x \odot_\beta y = x + y $$ So the multiplication is always the usual \(+\) on \((-\infty,\infty]\) — yes, I know this is confusing — while the addition is some more complicated operation that depends on \(\beta\). We get different rig structures on \((-\infty,\infty]\) for different values of \(\beta \gt 0\), but these rigs are all isomorphic because we got them all from the same rig structure on \([0,\infty)\).
However, now we can take the limit as \(\beta \to +\infty\) and get operations we call \(\oplus_\infty\) and \(\odot_\infty\). If we work these out we get $$ x \oplus_\infty y = x \, \min \, y $$
$$ x \odot_\infty y = x + y $$ These give a rig structure on \((-\infty,\infty]\) that's not isomorphic to any of those for finite \(\beta\). This is the tropical rig.
(Other people define the tropical rig differently, using different conventions, but usually theirs are isomorphic to this one.)
In classical statistical mechanics, a physical system has many states, each with its own energy \(E \in (-\infty,\infty]\). The unnormalized probability that the system is in a state of energy \(E\) is $$ f_\beta(E) = e^{-\beta E} $$ The case of infinite energy is not ordinarily considered, but it's allowed by the the math here, and this gives an unnormalized probability of zero.
We can reason with these unnormalized probabilities using addition and multiplication — or, equivalently, we can work directly with the energies \(E\) using the operations \(\oplus_\beta\) and \(\odot_\beta\) on \( (-\infty,\infty]\).
In short, we've enhanced the usual machinery of probability theory by working with unnormalized probabilities, and then transferred it over to the world of energies.
First, what's \(\beta\)? In physics we usually take $$ \beta = \frac{1}{k T} $$ where \(T\) is temperature and \(k\) is Boltzmann's constant. Boltzmann's constant has units of energy/temperature — it's about \(1.38 \cdot 10^{-23}\) joules per kelvin — so in physics we use it to convert between energy and temperature. \(k T\) has units of energy, so \(\beta\) has units of 1/energy, and \(\beta E\) is dimensionless. That's important: we're only allowed to exponentiate dimensionless quantities, and we want \(e^{-\beta E}\) to make sense.
One can imagine doing physics using some interpretation of the deformation parameter \(\beta\) other than \(1/k T\). But let's take \(\beta\) to be \(1/k T\). Then we can still understand the \(\beta \to +\infty\) limit in more than one way! We can
We could also try other things, like simply letting \(k\) and \(T\) do whatever they want as long as their product approaches zero. But let's just consider these two options.
It's sad that we get the tropical rig as a low-temperature limit: it should have been called the arctic rig! But the physics works out well. At temperature \(T\), systems in classical statistical mechanics minimize their free energy \(E - T S\) where \(E\) is energy and \(S\) is entropy. As \(T \to 0\), free energy reduces to simply the energy, \(E\). Thus, in the low temperature limit, such systems always try to minimize their energy! In this limit we're doing classical statics: the classical mechanics of systems at rest.
These ideas let us develop this analogy:
| taking the \(\hbar \to 0\) limit of | taking the \(T \to 0\) limit of |
| Quantum Mechanics | Classical Statistical Mechanics |
| gives | gives |
| Classical Mechanics | Classical Statics |
Blake Pollard and I explored this analogy extensively, and discovered some exciting things:
Second, there's a detailed analogy between classical mechanics and thermodynamics, which I explored here:
Most of this was about how classical mechanics and thermodynamics share common mathematical structures, like symplectic and contact geometry. These structures arise naturally from variational principles: principle of least action in classical mechanics, and the principle of maximum entropy in thermodynamics. By the end of this series I had convinced myself that thermodynamics should appear as the \(k \to 0\) limit of some physical framework, just as classical mechanics appears as the \(\hbar \to 0\) limit of quantum mechanics. So, let's look at option 2.
But what would it really mean to let \(k \to 0\)? Well, first let's remember what it would mean to let \(\hbar \to 0\).
I'll pick a specific real-world example: a laser beam. Suppose you're a physicist from 1900 who doesn't know quantum mechanics, who is allowed to do experiments on a beam of laser light. If you do crude measurements, this beam will look like a simple solution to the classical Maxwell equations: an electromagnetic field oscillating sinusoidally. So you will think that classical physics is correct. Only when you do more careful measurements will you notice that this wave's amplitude and phase are a bit 'fuzzy': you get different answers when you repeatedly measure these, no matter how good the beam is and how good your experimental apparatus is. These are 'quantum fluctuations', related to the fact that light is made of photons.
The product of the standard deviations of the amplitude and phase is bounded below by something proportional to \(\hbar\). So, we say that \(\hbar\) sets the scale of the quantum fluctuations. If we could let \(\hbar \to 0\), these fluctuations would become ever smaller, and in the limit the purely classical description of the situation would be exact.
Something similar holds with Boltzmann's constant. Suppose you're a physicist from 1900 who doesn't know about atoms, who has somehow been given the ability to measure the pressure of a gas in a sealed container with arbitrary accuracy. If you do crude measurements, the pressure will seem to be a function of the temperature, the volume of the container, and the amount of gas in the container. This will obey the laws of thermodynamics. Only when you do extremely precise experiments will you notice that the pressure is fluctuating. These are 'thermal fluctuations', caused by the gas being made of molecules.
The variance of the pressure is proportional to \(k\). So, we say that \(k\) sets the scale of the thermal fluctuations. If we could let \(k \to 0\), these fluctuations would become ever smaller, and in the limit the thermodynamics description of the situation would be exact.
The analogy here is a bit rough at points, but I think there's something to it. And if you examine the history, you'll see some strikin parallels. Einstein discovered that light is made of photons: he won the Nobel prize for his 1905 paper on this, and it led to a lot of work on quantum mechanics. But Einstein also wrote a paper in 1905 showing how to prove that liquid water is made of atoms! The idea was to measure the random Brownian motion of a grain of pollen in water — that is, thermal fluctuations. In 1908, Jean Perrin carried out this experiment, and he later won the Nobel "for his work on the discontinuous structure of matter". So the photon theory of light and the atomic theory of matter both owe a lot to Einstein's work.
Planck had earlier introduced what we now call Planck's constant in his famous 1900 paper on the quantum statistical mechanics of light, without really grasping the idea of photons. Remarkably, this is also the paper that first introduced Boltzmann's constant \(k\). Boltzmann had the idea that entropy was proportional to the logarithm of the number of occupied states, but he never estimated the constant of proportionality or gave it a name: Planck did both! So Boltzmann's constant and Planck's constant were born hand in hand.
There's more to say about how to correctly take the \(\hbar \to 0\) limit of a laser beam: we have to simultaneously increase the expected number of photons, so that the rough macroscopic appearance of the laser beam remains the same, rather than becoming dimmer. Similarly, we have to be careful when taking the \(k \to 0\) limit of a container of gas: we need to also increase the number of molecules, so that the average pressure remains the same instead of decreasing.
Getting these details right has exercised me quite a bit lately: I'm trying to develop a general theory of the \(k \to 0\) limit, but it's been essential to work through some examples. I'll talk about one next time.
September 7, 2024
I'm trying to work out how classical statistical mechanics can reduce to thermodynamics in a certain limit. I sketched out the game plan in Part 1 but there are a lot of details to hammer out. While I'm doing this, let me stall for time by explaining more precisely what I mean by 'thermodynamics'. Thermodynamics is a big subject, but I mean something more precise and limited in scope.
Definition. A thermostatic system is a convex space \(X\) together with a concave function \(S \colon X \to [-\infty,\infty]\). We call \(X\) the space of states, and call \(S(x)\) the entropy of the state \(x \in X\).
There's a lot packed into this definition:
Here's what people do in this very simple setting. Our thermostatic system is a concave function $$ S \colon \mathbb{R} \to [-\infty, \infty] $$ describing the entropy \(S(E)\) of our system when it has energy \(E\). But often entropy is also a strictly increasing function of energy, with \(S(E) \to \infty\) as \(E \to \infty\). In this case, it's impossible for a system to literally maximize entropy. What it does instead is maximize 'entropy minus how much it spends on energy' — just as you might try to maximize the pleasure you get from eating doughnuts minus your displeasure at spending money. Thus, if \(C\) is the 'cost' of energy, our system tries to maximize $$ S(E) - C E $$ The cost \(C\) is the reciprocal of a quantity called temperature: $$ C = \frac{1}{T} $$ So, \(C\) should be called inverse temperature, and the rough intuition you should have is this. When it's hot, energy is cheap and our system's energy can afford to be high. When it's cold, energy costs a lot and our system will not let its energy get too high. If \(S(E) - C E\) as a function of \(E\) is differentiable and has a maximum, the maximum must occur at a point where $$ \frac{d}{d E} \left(S(E) - C E \right) = 0 $$ or $$ \frac{d}{d E} S(E) = C $$ This gives the fundamental relation between energy, entropy and temperature: $$ \frac{d}{d E} S(E) = \frac{1}{T} $$ However, the math will work better for us if we use the inverse temperature. Suppose we have a system maximizing \(S(E) - C E\) for some value of \(C\). The maximum value of \(S(E) - C E \) is called free entropy and denoted \(\Phi\). In short: $$ \Phi(C) = \sup_E \left(S(E) - C E \right) $$ or if you prefer $$ -\Phi(C) = \inf_E \left(C E - S(E) \right) $$ This way of defining \(-\Phi\) in terms of \(S\) is called a Legendre–Fenchel transform, though conventions vary about the precise definition of this transform, and also its name. Since I'm lazy, I'll just call it the Legendre transform. For more, read this:
The great thing about Legendre transforms is that if a function is convex and lower semicontinuous, when you take its Legendre transform twice you get that function back! This is part of the Fenchel–Moreau theorem. So under these conditions we automatically get another formula that looks very much like the one we've just seen: $$ S(E) = \inf_C \left(C E + \Phi(C) \right) $$ When \(C E + \Phi(C)\) has a minimum as a function of \(C\) and it's differentiable there, this minimum must occur at a point where $$ \frac{d}{d C} \left(C E + \Phi(C) \right) = 0 $$ or $$ \frac{d}{d C} \Phi(C) = -E $$When we describe a thermostatic system as a limit of classical statistical mechanical systems, these are the formulas we'd like to see emerge in the limit!
I've been treating entropy as a function of energy: this is the so-called entropy scheme. But it's traditional to treat energy as a function of entropy: this is called the energy scheme.
The entropy scheme generalizes better. In thermodynamics we often want to think about situations where entropy is a function of several variables: energy, volume, the amounts of various chemicals, and so on. Then we should work with a thermostatic system \(S \colon X \to [-\infty,\infty]\) where \(X\) is a convex subset of \(\mathbb{R}^n\). Everything I did generalizes nicely to that situation, and now \(\Psi\) will be one of \(n\) quantities that arise by taking a Legendre transform of \(S\).
But when entropy is a function of just one variable, energy, people often turn the tables and try to treat energy as a function of entropy, say \(E(S)\). They then define the free energy as a function of temperature by $$ F(T) = \inf_S (E(S) - T S) $$ This is essentially a Legendre transform — but notice that inside the parentheses we have \(E(S) - T S\) instead of \(T S - E(S)\). We can fix this by using a sup instead of an inf, and writing $$ -F(T) = \sup_S (T S - E(S)) $$ It's actually very common to define the Legendre transform using a sup instead of an inf, so that's fine. The only wrinkle is that this Legendre transform gives us \(-F\) instead of \(F\).
When the supremum is achieved at a point where \(E\) is differentiable we have $$ \displaystyle{ \frac{d}{d S} E(S) = T } $$ at that point. When \(E\) is concave and lower semicontinuous, taking its Legendre transform twice gets us back where we started: $$ E(S) = \sup_T (T S + F(T)) $$ And when this supremum is achieved at a point where \(F\) is differentiable, we have $$ \displaystyle{ \frac{d}{d T} F(T) = - S } $$ To top it off, physicists tend to assume \(S\) and \(T\) take values where the suprema above are achieved, and not explicitly write what is a function of what. So they would summarize everything I just said with these equations: $$ F = E - T S , \qquad E = T S + F $$ $$ \displaystyle{ \frac{d F}{d T} = - S , \qquad \frac{d S}{d E} = T } $$ If instead we take the approach I've described, where entropy is treated as a function of energy, it's natural to focus on the negative free entropy \(\Psi\) and inverse temperature \(C\). If we write the equations governing these in the same slapdash style as those above, they look like this: $$ \Psi = C E - S, \qquad S = C E - \Psi $$ $$ \displaystyle{ \frac{d \Psi}{d C} = E, \qquad \frac{d S}{d E} = C } $$ Less familiar, but more symmetrical! The two approaches are related by $$ \displaystyle{ C = \frac{1}{T}, \qquad \Psi = \frac{F}{T} } $$
In Part 2, I explained a bit of thermodynamics. We saw that some crucial formulas involve Legendre transforms, where you take a function \(f \colon \mathbb{R} \to [-\infty,\infty]\) and define a new one \(\tilde{f} \colon \mathbb{R} \to [-\infty,\infty]\) by $$ \tilde{f}(s) = \inf_{x \in \mathbb{R}} (s x - f(x)) $$ I'd like the Legendre transform to be something like a limit of the Laplace transform, where you take a function \(f\) and define a new one \(\hat{f}\) by $$ \hat{f}(s) = \int_{-\infty}^\infty e^{-s x} f(x) \, d x $$ Why do I care? As we'll see later, classical statistical mechanics features a crucial formula that involves a Laplace transform. So it would be great if we could find some parameter \(\beta\) in that formula, take the limit \(\beta \to +\infty\), and get a corresponding equation in thermodynamics that involves a Legendre transform!
As a warmup, let's look at the purely mathematical question of how to get the Legendre transform as a limit of the Laplace transform — or more precisely, something like the Laplace transform. Once we understand that, we can tackle the physics in a later post.
Suppose we want to define a notion of integration with \(\oplus_\beta\) replacing ordinary addition. We could call it '\(\beta\)-integration' and denote it by \(\int_\beta\). Then it's natural to try this: $$ \int_\beta f(x) \, d x = - \frac{1}{\beta} \ln \int e^{-\beta f(x)} d x $$ If the function \(f\) is nice enough, we could hope that $$ \lim_{\beta \to +\infty} \int_\beta f(x) \, d x \; = \; \inf_x f(x) $$ Then, we could hope to express the Legendre transform $$ \tilde{f}(s) = \inf_{x \in \mathbb{R}} (s x - f(x)) $$ as the \(\beta \to + \infty\) limit of some transform involving \(\beta\)-integration.
Indeed, in Section 6 here, Litvinov claims that the Legendre transform is the \(\beta = \infty\) analogue of the Laplace transform:
Almost Proved Theorem. Suppose that \(f \colon [0,\infty) \to \mathbb{R}\) is a concave function with continuous second derivative. Suppose that for some \(s \gt 0 \) the function \(s x - f(x)\) has a unique minimum at \(x_0\), and \(f''(x_0) \lt 0\). Then as \(\beta \to +\infty\) we have $$ \displaystyle{ -\frac{1}{\beta} \ln \int_0^\infty e^{-\beta (s x - f(x))} \, d x \quad \longrightarrow \quad \inf_x \left( s x - f(x)\right) } $$
Almost Proof. Laplace's method should give the asymptotic formula $$ \displaystyle{ \int_0^\infty e^{-\beta (s x - f(x))} \, d x \quad \sim \quad \sqrt{\frac{2\pi}{-\beta f''(x_0)}} \; e^{-\beta(s x_0 - f(x_0)} } $$ Taking the logarithm of both sides and dividing by \(-\beta\) we get $$ \displaystyle{\lim_{\beta \to +\infty} -\frac{1}{\beta} \ln \int_0^\infty e^{-\beta(s x - f(x))} \, d x \; = \; s x_0 - f(x_0) } $$ since $$ \displaystyle{ \lim_{\beta \to +\infty} \frac{1}{\beta} \; \ln \sqrt{\frac{2\pi}{-\beta f''(x_0)}} = 0 } $$ Since \(s x - f(x)\) has a minimum at \(x_0\) we get the desired result: $$ \displaystyle{ -\frac{1}{\beta} \ln \int_0^\infty e^{-\beta (s x - f(x))} \, d x \quad \longrightarrow \quad \inf_x \left( s x - f(x)\right) } $$ The only tricky part is that Laplace's method as proved here requires finite limits of integration, while we are integrating from \(0\) all the way up to \(\infty\). However, the function \(s x - f(x)\) is concave, with a minimum at \(x_0\), and it has positive second derivative there since \(f''(x_0) \lt 0\). Thus, it grows at least linearly for large \(x\), so as \(\beta \to +\infty\) the integral $$ \displaystyle \int_0^\infty e^{-\beta(s x - f(x))} \, d x $$ can be arbitrarily well approximated by an integral over some finite range \([0,a]\). ∎
Someone must have studied the hell out of this issue somewhere — do you know where?
Now, let's look at the key quantity in the above result: $$ \displaystyle{ - \frac{1}{\beta} \ln \int_0^\infty e^{-\beta (s x - f(x))} \, d x } $$ We've got a \(-1/\beta\) and then the logarithm of an integral that is not exactly a Laplace transform... but it's close! In fact it's almost the Laplace transform of the function $$ g_\beta(x) = e^{\beta f(x)} $$ since $$ \displaystyle{ \int_0^\infty e^{-\beta (s x - f(x))} \, d x = \int_0^\infty e^{-\beta s x} \, g_\beta(x) \, d x } $$ The right hand side here would be the Laplace transform of \(g_\beta\) if it weren't for that \(\beta\) in the exponential.
So, it seems to be an exaggeration to say the Legendre transform is a limit of the Laplace transform. It seems to be the limit of something that's related to a Laplace transform, but more complicated in a number of curious ways.
This has made my life difficult (and exciting) for the last few weeks. Right now I believe that all the curious complications do exactly what we want them to in our physics applications. But I should hold off on declaring this until I write up all the details: I keep making computational mistakes and fixing them, with a roller-coaster of emotions as things switch between working and not working.
September 16, 2024
In Part 1, I explained my hopes that classical statistical mechanics reduces to thermodynamics in the limit where Boltzmann's constant \(k\) approaches zero. In Part 2, I explained exactly what I mean by 'thermodynamics'. I also showed how, in this framework, a quantity called 'negative free entropy' arises as the Legendre transform of entropy.
In Part 3, I showed how a Legendre transform can arise as a limit of something like a Laplace transform.
Today I'll put all the puzzle pieces together. I'll explain exactly what I mean by 'classical statistical mechanics', and how negative free entropy is defined in this framework. Its definition involves a Laplace transform. Finally, using the result from Part 3, I'll show that as \(k \to 0\), negative free entropy in classical statistical mechanics approaches the negative free entropy we've already seen in thermodynamics!
I focused on the simple case where the macrostate is completely characterized by a single macroscopic observable called its energy \(E \in [0,\infty)\). In this case the space of macrostates is \(X = [0,\infty)\). If we can understand this case, we can generalize later.
In classical statistical mechanics we go further and consider the set \(\Omega\) of microstates of a system. The microstate specifies all the microscopic details of a system! For example, if our system is a canister of helium, a microstate specifies the position and momentum of each atom. Thus, the space of microstates is typically a high-dimensional manifold — where by 'high' I mean something like \(10^{23}\). On the other hand, the space of macrostates is often low-dimensional — where by 'low' I mean something between 1 and 10.
To connect thermodynamics to classical statistical mechanics, we need to connect macrostates to microstates. The relation is that each macrostate is a probability distribution of microstates: a probability distribution that maximizes entropy subject to constraints on the expected values of macroscopic observables.
To see in detail how this works, let's focus on the simple case where our only macroscopic observable is energy.
It gets tiring to say 'classical statistical mechanical system', so I'll abbreviate this as classical stat mech system.
When we macroscopically measure the energy of a classical stat mech system to be \(E\), what's really going on is that the system is in a probability distribution of microstates for which the expected value of energy is \(E\). A probability distribution is defined to be a measurable function $$ p \colon \Omega \to [0,\infty) $$ with $$ \displaystyle{ \int_\Omega p(x) \, d\mu(x) = 1 } $$ The expected energy in this probability distribution is defined to be $$ \displaystyle{ \langle H \rangle = \int_\Omega H(x) \, p(x) \, d \mu(x) } $$ So what I'm saying is that \(p\) must have $$ \langle H \rangle = E $$ But lots of probability distributions have \(\langle H \rangle = E\). Which one is the physically correct one? It's the one that maximizes the Gibbs entropy: $$ \displaystyle{ S = - k \int_\Omega p(x) \, \ln p(x) \, d\mu(x) }$$ Here \(k\) is a unit of entropy called Boltzmann's constant. Its value doesn't affect which probability distribution maximizes the entropy! But it will affect other things to come.
Now, there may not exist a probability distribution \(p\) that maximizes \(S\) subject to the constraint \(\langle H \rangle = E\), but there often is — and when there is, we can compute what it is. If you haven't seen this computation, you can find it in my book What is Entropy? starting on page 24. The answer is the Boltzmann distribution: $$ \displaystyle{ p(x) = \frac{e^{-C H(x)/k}}{\int_\Omega e^{-C H(x)/k} \, d \mu(x)} } $$ Here \(C\) is a number called the inverse temperature. We have to cleverly choose its value to ensure \(\langle H \rangle = E\). That might not even be possible. But if we get that to happen, \(p\) will be the probability distribution we seek.
The normalizing factor in the formula above is called the partition function $$ Z_k(C) = \int_\Omega e^{-C H(x)/k} \, d\mu(x) $$ and it turns out to be important in its own right. The integral may not always converge, but when it does not we'll just say it equals \(+\infty\), so we get $$ Z_k \colon [0,\infty) \to [0,\infty] $$ One reason the partition function is important is that $$ - k \ln Z_k(C) = C \langle H \rangle - S $$ where \(\langle H \rangle\) and \(S\) are computed using the Boltzmann distribution for the given value of \(C\) For a proof see pages 67–71 of my book, though beware that I use different notation. The quantity above is called the negative free entropy of our classical stat mech system. In my book I focus on a closely related quantity called the 'free energy', which is the negative free entropy divided by \(C\). Also, I talk about \(\beta = 1/k T\) instead of the inverse temperature \(C = 1/T\).
Let's call the negative free entropy \(\Psi_k(C)\), so $$ \displaystyle{ \Psi_k(C) = -k \ln Z_k(C) = - k \ln \int_\Omega e^{-C H(x)/k} \, d\mu(x) } $$ I've already discussed negative free entropy in Part 2, but that was for thermostatic systems, and it was defined using a Legendre transform. This new version of negative free entropy applies to classical stat mech systems, and we'll see it's defined using a Laplace transform. But they're related: we'll see the limit of the new one as \(k \to 0\) is the old one!
First, given a classical stat mech system with measure space \((\Omega, \mu)\) and Hamiltonian \(H \colon \Omega \to \mathbb{R}\), let
$$ \nu(E) = \mu(\{x \in \Omega \vert \; H(x) \le E \} $$
be the measure of the set of microstates with energy \(\le E\). This is an increasing function of \(E \in \mathbb{R}\) which is right-continuous, so it defines a Lebesgue--Stieltjes measure \( \nu \) on the real line. Yes, I taught real analysis for decades and always wondered when I'd actually use this concept in my own work: today is the day! ![]()
The reason I care about this measure \(\nu\) is that it lets us rewrite the partition function as an integral over the nonnegative real numbers: $$ \displaystyle{ Z_k(C) = \int_0^\infty e^{-C E/k} \, d\nu(E) } $$ Very often the measure \(\nu\) is absolutely continuous, which means that $$ d\nu(E) = g(E) \, d E $$ for some locally integrable function \(g \colon \mathbb{R} \to \mathbb{R}\). I will assume this from now on. We thus have $$ \displaystyle{ Z_k(C) = \int_0^\infty e^{-C E/k} \, g(E) \, d E } $$ Physicists call \(g\) the density of states because if we integrate it over some interval \([E, E + \Delta E]\) we get 'the number of states' in that energy range. At least that's what physicists say. What we actually get is the measure of the set $$ \{x \in X: \; E \le H(x) \le E + \Delta E \} $$ Before moving on, a word about dimensional analysis. I'm doing physics, so my quantities have dimensions. In particular, \(E\) and \(d E\) have units of energy, while the measure \(d\nu(E)\) is dimensionless, so the density of states \(g(E)\) has units of energy-1.
This matters because right now I want to take the logarithm of \(g(E)\), yet the rules of dimensional analysis include a stern finger-wagging prohibition against taking the logarithm of a quantity unless it's dimensionless. There are legitimate ways to bend these rules, but I won't. Instead I'll follow most physicists and introduce a constant with dimensions of energy, \(w\), called the energy width. It's wise to think of this as an arbitrary small unit of energy. Using this we can make all the calculations to come obey the rules of dimensional analysis. If you find that ridiculous, you can mentally set \(w\) equal to 1.
With that said, now let's introduce the so-called microcanonical entropy, often called the Boltzmann entropy: $$ S_{\mathrm{micro}}(E) = k \ln (w g(E)) $$ Here we are taking Boltzmann's old idea of entropy as \(k\) times the logarithm of the number of states and applying it to the density of states. This allows us to define an entropy of our system at a specific fixed energy \(E\). Physicists call the set of microstates with energy exactly equal to some number \(E\) the microcanonical ensemble, and they say the microcanonical entropy is the entropy of the microcanonical ensemble. This is a bit odd, because the set of microstates with energy exactly \(E\) typically has measure zero. But it's a useful way of thinking.
In terms of the microcanonical entropy, we have $$ \displaystyle{ g(E) = \frac{1}{w} e^{S_{\mathrm{micro}}(E)/k} } $$ Combining this with our earlier formula $$ \displaystyle{ Z_k(C) = \int_0^\infty e^{-C E/k} g(E) \, d E } $$ we get this formula for the partition function: $$ \displaystyle{ Z_k(C) = \int_0^\infty e^{-(C E - S_{\mathrm{micro}}(E))/k} \, \frac{d E}{w} } $$ Now things are getting interesting! First, the quantity \(C E - S_{\mathrm{micro}}(E)\) should remind you of the formula we saw in Part 2 for the negative free entropy of a thermostatic system. Remember, that formula was $$ \Psi(C) = \inf_E (C E - S(E)) $$ Second, we instantly get a beautiful formula for the negative free entropy of a classical stat mech system: $$ \displaystyle{ \Psi_k(C) = - k \ln Z_k(C) = - k \ln \int_0^\infty e^{-(C E - S_{\mathrm{micro}}(E))/k} \, \frac{d E}{w} } $$ Now for the climax of this whole series so far. We can now prove that as \(k \to 0\), the negative free entropy of a classical stat mech system approaches the negative free entropy of a thermostatic system!
To state and prove this result, I will switch to treating the microcanonical entropy \(S_{\mathrm{micro}}\) as fundamental, rather than defining it in terms of the density of states. This means we can now let \(k \to 0\) while holding the function \(S_{\mathrm{micro}}\) fixed. I will also switch to units of energy where \(w = 1\). Thus, starting from \(S_{\mathrm{micro}}\), I will define the negative free entropy \(\Psi_k\) by $$ \displaystyle{ \Psi_k(C) = - k \ln \int_0^\infty e^{-(C E - S_{\mathrm{micro}}(E))/k} \, d E} $$ We can now study the limit of \(\Psi_k(C)\) as \(k \to 0\).
Main Result. Suppose \(S_{\mathrm{micro}} \colon [0,\infty) \to \mathbb{R}\) is a concave function with continuous second derivative. Suppose that for some \(C \gt 0\) the quantity \(C E - S_{\mathrm{micro}}(E)\) has a unique minimum as a function of \(E\), and \(S''_{\mathrm{micro}} \lt 0\) at that minimum. Then $$ \displaystyle{ \lim_{k \to 0} \Psi_k(C) \quad = \quad \inf_E \left(C E - S_{\mathrm{micro}}(E)\right) } $$ The quantity at right deserves to be called the microcanonical negative free entropy. So, when the hypotheses hold,
Here I've left off the word 'negative' twice, which is fine. But this sentence still sounds like a mouthful. Don't feel bad if you find it confusing. But it could be the result we need to see how classical statistical mechanics approaches classical thermodynamics as \(k \to 0\). So I plan to study this result further, and hope to explain it much better!
But today I'll just prove the main result and quit. I figure it's good to get the math done before talking more about what it means.
Next, we need a theorem from Part 3. My argument for that theorem was not a full mathematical proof — I explained the hole I still need to fill — so I cautiously called it an 'almost proved theorem'. Here it is:
Almost Proved Theorem. Suppose that \(f \colon [0,\infty) \to \mathbb{R}\) is a concave function with continuous second derivative. Suppose that for some \(s \gt 0 \) the function \(s x - f(x)\) has a unique minimum at \(x_0\), and \(f''(x_0) \lt 0\). Then as \(\beta \to +\infty\) we have
$$ \displaystyle{ \lim_{\beta \to +\infty} -\frac{1}{\beta} \ln \int_0^\infty e^{-\beta (s x - f(x))} \, d x \; = \; \inf_x \left( s x - f(x)\right) } $$
Now let's use this to prove our main result! To do this, take
$$ s = C, \quad x = E, \quad f(x) = S_{\mathrm{micro}}(E), \quad \beta = 1/k $$
Then we get
$$ \displaystyle{\lim_{k \to 0} - k \ln \int_0^\infty e^{(C E - S_{\mathrm{micro}}(E))/k} \, d E \quad = \quad \inf_E \left(C E - S_{\mathrm{micro}}(E) \right) } $$
and this is exactly what we want. ∎
September 26, 2024
In Part 4, I presented a nifty result supporting my claim that classical statistical mechanics reduces to thermodynamics when Boltzmann's constant \(k\) approaches zero. I used a lot of physics jargon to explain why I care about this result. I also used some math jargon to carry out my argument.
This may have been off-putting. But to understand the result, you only need to know calculus! So this time I'll state it without all the surrounding rhetoric, and then illustrate it with an example.
Main Result. Suppose \(S \colon [0,\infty) \to \mathbb{R}\) is a concave function with continuous second derivative. Suppose that for some \(C \gt 0\) the quantity \(C E - S(E)\) has a unique minimum as a function of \(E\), and \(S'' \lt 0\) at that minimum. Then for this value of \(C\) we have $$ \displaystyle{ \lim_{k \to 0} - k \ln \int_0^\infty e^{-(C E - S(E))/k} \; d E \quad = \quad \inf_E \left(C E - S(E)\right) } $$ when \(k\) approaches \(0\) from above.
I made up some names for the things on both sides of the equation: $$ \displaystyle{ \Psi_k(C) = - k \ln \int_0^\infty e^{-(C E - S(E))/k} \; d E } $$ and $$ \Psi(C) = \inf_E \left(C E - S(E)\right) $$ So, the result says $$ \lim_{k \to 0} \Psi_k(C) = \Psi(C) $$ when the hypotheses hold.
So, let's show $$ \lim_{k \to 0} \Psi_k(C) = \Psi(C) $$ in this case. Of course this follows from what I'm calling the 'main result' — but working through this example really helped me. While struggling with it, I discovered some confusion in my thinking! Only after straightening this out was I able to get this example to work.
I'll say more about the physics of this example at the end of this post. For now, let's just do the math.
First let's evaluate the left hand side, \(\lim_{k \to 0} \Psi_k(C)\). By definition we have $$ \displaystyle{ \Psi_k(C) = - k \ln \int_0^\infty e^{-(C E - S(E))/k} \; d E } $$ Plugging in \(S(E) = \alpha \ln E\) we get this: $$ \begin{array}{ccl} \Psi_k(C) &=& \displaystyle{ - k \ln \int_0^\infty e^{-(C E - \alpha \ln E)/k} \; d E } \\ \\ &=& \displaystyle{ - k \ln \int_0^\infty e^{-C E/k} \; E^{\alpha/k} \; d E } \end{array} $$ To evaluate this integral we can use the formula $$ \displaystyle{ \int_0^\infty e^{-x} \, x^n \; d x = n! } $$ which makes sense for all positive numbers, even ones that aren't integers, if we interpret \(n!\) using the gamma function. So, let's use this change of variables: $$ x = C E/k , \qquad E = k x/C $$ We get $$ \begin{array}{ccl} \Psi_k(C) &=& \displaystyle{ - k \ln \int_0^\infty e^{-C E/k} \; E^{\alpha/k} \; d E } \\ \\ &=& \displaystyle{ - k \ln \int_0^\infty e^{-x} \; \left( \frac{k x}{C} \right)^{\alpha/k} \, \frac{k d x}{C} } \\ \\ &=& \displaystyle{ - k \ln \left( \left( \frac{k}{C} \right)^{\frac{\alpha}{k} + 1} \int_0^\infty e^{-x} x^{\alpha/k} \, d x \right) } \\ \\ &=& \displaystyle{ - k \left(\frac{\alpha}{k} + 1\right) \ln \frac{k}{C} - k \ln \left(\frac{\alpha}{k}\right)! } \\ \\ &=& \displaystyle{ -\left(\alpha + k \right) \ln \frac{k}{C} - k \ln \left(\frac{\alpha}{k}\right)! } \end{array} $$ Now let's take the \(k \to 0\) limit. For this we need Stirling's formula $$ n! \sim \sqrt{2 \pi n} \left(\frac{n}{e}\right)^n $$ or more precisely this version: $$ \ln n! = n \ln \frac{n}{e} + O(\ln n) $$ Let's compute: $$ \begin{array}{ccl} \lim_{k \to 0} \Psi_k(C) &=& \displaystyle{ \lim_{k \to 0} \left( -\left(\alpha + k \right) \ln \frac{k}{C} - k \ln \left(\frac{\alpha}{k}\right)! \right) } \\ \\ &=& \displaystyle{ -\lim_{k \to 0} \left(\alpha \ln \frac{k}{C} \; + \; k \ln \left(\frac{\alpha}{k}\right)! \right) } \\ &=& \displaystyle{ -\lim_{k \to 0} \left(\alpha \ln \frac{k}{C} \; + \; k \left(\frac{\alpha}{k} \ln \frac{\alpha}{e k} + O\left(\ln \frac{\alpha}{k} \right) \right) \right) } \\ &=& \displaystyle{ -\alpha \ln \frac{k}{C} - \alpha \ln \frac{\alpha}{e k} } \\ &=& \displaystyle{ \alpha \ln \frac{e C}{\alpha} } \\ \end{array} $$ Now let's compare the right hand side of the main result. By definition this is $$ \Psi(C) = \inf_E \left(C E - S(E)\right) $$ Plugging in \(S(E) = \alpha \ln E\) we get this: $$ \Psi(C) = \inf_E \left(C E - \alpha \ln E \right) $$ Since \(\alpha \gt 0\), the function \(C E - \alpha \ln E\) has strictly positive second derivative as a function of \(E\) wherever it's defined, namely \(E \gt 0\). It also has a unique minimum. To find this minimum we solve $$ \frac{d}{d E} \left(C E - \alpha \ln E \right) = 0 $$ which gives $$ C - \frac{\alpha}{E} = 0 $$ or $$ E = \frac{\alpha}{C} $$ We thus have $$ \Psi(C) = C \cdot \frac{\alpha}{C} - \alpha \ln \frac{\alpha}{C} = \alpha\left(1 - \ln \frac{\alpha}{C} \right) $$ or $$ \Psi(C) = \alpha \ln \frac{e C}{\alpha} $$ Yes, we've seen this before. So we've verified that $$ \lim_{k \to 0} \Psi_k(C) = \Psi(C) $$ in this example.
For any system of this sort, its temperature is proportional to its energy. We saw this fact today when I showed the infimum in this formula: $$ \Psi(C) = \inf_E \left(C E - S(E)\right) $$ occurs at \(E = \alpha/C\). The quantity \(C\) is the 'coldness' or inverse temperature \(C = 1/T\), so we're seeing \(E = \alpha T\). This type of result fools some students into thinking temperature is always proportional to energy! That's obviously false: think about how much more energy it take to melt an ice cube than it takes to raise the temperature of the melted ice cube by a small amount. So we're dealing with a very special, simple sort of system here.
In equilibrium, a system at fixed coldness will choose the energy that maximizes \(S(E) - C E\). The maximum value of this quantity is called the system's 'free entropy'. In other words, the system's negative free entropy is \(\Psi(C) = \inf_E \left(C E - S(E)\right)\).
All of my physics remarks so far concern 'thermostatics' as defined in Part 2. In this approach, we start with entropy as a function of energy, and define \(\Psi(C)\) using a Legendre transform. Boltzmann's constant never appears in our calculations.
But we can also follow another approach: 'classical statistical mechanics', as defined in Part 4. In this framework we define negative free entropy in a different way. We call \(\exp(S(E)/k)\) the 'density of states', and we define negative free entropy using the Laplace transform of the density of states. It looks like this: $$ \displaystyle{ \Psi_k(C) = - k \ln \int_0^\infty e^{-(C E - S(E))/k} \; d E } $$ In this approach, Boltzmann's constant is important. However, the punchline is that $$ \lim_{k \to 0} \Psi_k(C) = \Psi(C) $$ Thus classical statistical mechanics reduces to thermostatics as \(k \to 0\), at least in this one respect.
In fact various other quantities should work the same way. We can define them in classical statistical mechanics, where they depend on Boltzmann's constant, but as \(k \to 0\) they should approach values that you could compute in a different way, using thermostatics. So, what I'm calling the 'main result' should be just one case of a more general result. But this one case clearly illustrates the sense in which the Laplace transform reduces to the Legendre transform as \(k \to 0\). This should be a key aspect of the overall story.
In 1596, Kepler claimed that the planetary orbits would only follow "God's design" if there were two more planets: one between Mars and Jupiter and one between Mercury and Venus. Later folks came up with the Titius–Bode law. This says that for each n there should be a planet whose distance from the Sun is
So, starting in 1800, a team of twenty-four astronomers called the "celestial police" looked between Mars and Jupiter. And in 1801 one of them, a priest named Giuseppe Piazzi, found an object in the right place! Later, other members of the celestial police found other asteroids in a belt between Mars and Jupiter. But the first to be found was the biggest: Ceres.
In 2015, the human race sent a probe called Dawn to investigate Ceres. I wrote about it in my September 13, 2015 diary entry! And it found something wonderful.
The surface of Ceres is a mix of ice and hydrated minerals like carbonates and even clay! If you haven't thought much about clay, let me just say that most clay on Earth is produced by the erosion of rocks by water. In fact I even read somewhere that most clay was formed after the rise of lichens and plants, since they're so good at breaking down rock.
Ceres probably doesn't have an internal ocean of liquid water like Jupiter's moon Europa. But it seems that brine still flows through its outer mantle and reaches the surface!
Here is one artist's image, from NASA:
Now a new paper argues that Ceres contains a lot of ice, and was once an ocean-covered world. This was formerly thought impossible. One of authors, Mike Sori, says:
We think that there's lots of water-ice near Ceres surface, and that it gets gradually less icy as you go deeper and deeper. People used to think that if Ceres was very icy, the craters would deform quickly over time, like glaciers flowing on Earth, or like gooey flowing honey. However, we've shown through our simulations that ice can be much stronger in conditions on Ceres than previously predicted if you mix in just a little bit of solid rock.Here's the paper:
And here's where I got that quote:
By the way, did you notice something funny about the Titius–Bode law? I left out Mercury! You get Mercury's orbit if you set n = -∞. This means Kepler was sort of right, but also sort of wrong. If you allow negative integers n, the Titius–Bode law predicts an infinite sequence of planets between Mercury and Venus, with smaller and smaller orbits whose radii approaches that of Mercury.
Also by the way, most astrophysicist aren't fully convinced by any of the theories put forth for why the Titius–Bode law should work. For more, try this: