
Go, team, go!
Just when I feel we're doomed I see something that gives me hope. It's an emotional rollercoaster. But this particular rollercoaster is rolling downhill fast. Wheee!
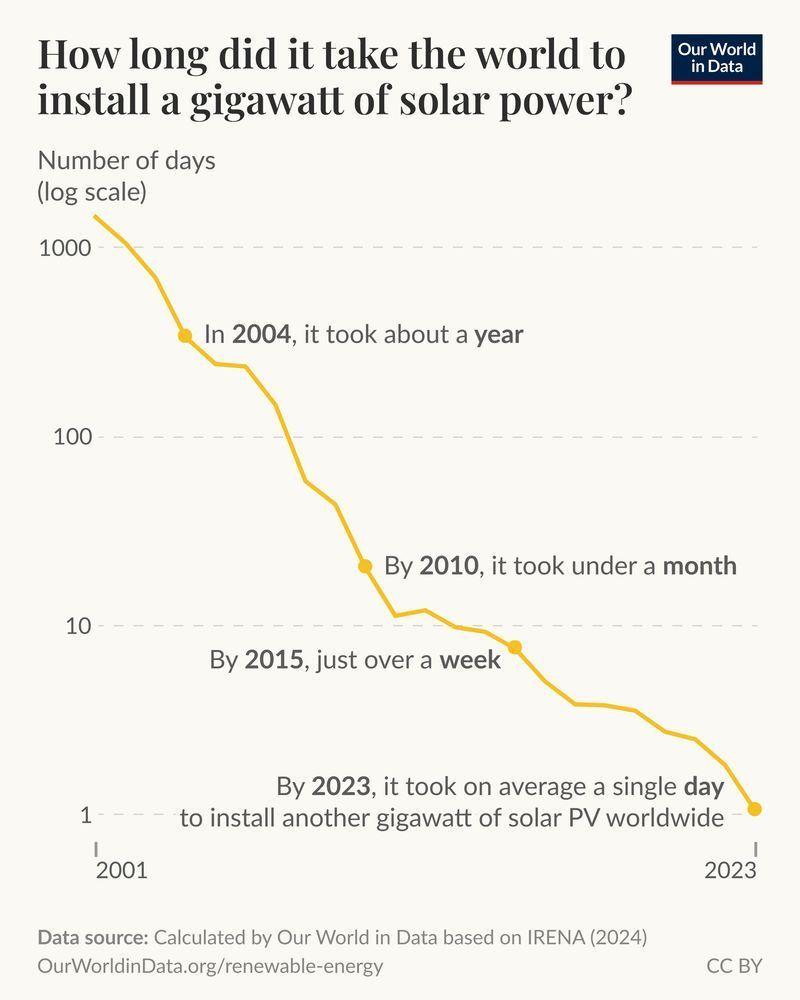
From here:
A grid-scale battery in the Scottish Highlands got a chance to prove its mettle in March when, 11 days after it started up, a massive wood-burning generator in Northern England shut down unexpectedly. Suddenly 1,877 megawatts of supply was missing, causing the 50-hertz frequency of the grid’s alternating current to crash below its 49.8-Hz operating limit in just 8 seconds.The article goes on to explain a bit more about how these batteries work and why they're so important for the solar- and wind-powered future. (Amusing that it was unreliable wood power needing help this time. England is so backward in some ways.)But the new 200-MW battery station leapt into action within milliseconds, releasing extra power to help arrest the frequency collapse and keep the grid running.
Conventional fossil-fuel generators have historically helped thwart these kinds of problems. With the inertia of their spinning rotors, their kinetic energy provides a buffer against rapid swings in frequency and voltage. But the response in the Highlands was one of the world’s first examples of a grid-scale battery commissioned to do this kind of grid-stabilizing job.
Without moving parts, the lithium battery storage site—the largest in Europe and located in Blackhillock, Scotland—simulates inertia using power electronics. And in an innovative twist, the battery site can also provide short-circuit current in response to a fault, just like conventional power generators.
Four more of these battery sites are under construction in Scotland.

The 'cat gap' is a period of time with very few fossils of cats, from 25 million to 18.5 million years ago:
For example, the old 'false saber-tooth cats' are not closely related to the more recent saber-tooth cats like Smilodon, who lived in the New World until almost 8,200 years ago.
September 14, 2025
The little red dots in the early universe could be 'quasi-stars'.
Calculations show a quasi-star could form when a gas cloud over 1,000 times the Sun's mass collapses and forms a black hole. Its outer layers would be big enough to absorb the resulting supernova without being blown apart! Then you'd get a huge star powered not by fusion but by gravity, with a black hole in its center.
Such a star could be as luminous as a small present-day galaxy! And that's what little red dots are like.
As a quasi-star ages, it should cool down, and eventually the gas on the outside would dissipate, leaving behind a black hole. Such 'intermediate-mass black holes' could be the ancestors of the supermassive black holes we now see in most galaxies. This would solve a mystery: we don't know how such big black holes arose.
Pro tip:
Don't embarrass yourself by mixing up a quasi-star with a Thorne–Żytkow object! That's when a neutron star falls into an ordinary large star. We may have seen one of those in the Small Magellanic Cloud, a small galaxy orbiting the Milky Way.
September 13, 2025
It's well known that you can construct the octonions using triality. One statement of triality is that \(\text{Spin}(8)\) has nontrivial outer automorphisms of order 3. On the other hand, the octonions have nontrivial inner automorphisms of order 3. My question:
The second fact is perhaps not very well known. It may even be hard to understand what it means. Though the octonions are nonassociative, for any nonzero octonion \(g\) the map
$$ \begin{array}{rccl} f \colon & \mathbb{O} &\to& \mathbb{O} \\ & x & \mapsto & g x g^{-1} \end{array} $$
is well-defined, since \((g x)g^{-1} = g(x g^{-1})\), which one can show using the fact that the octonions are alternative. More surprisingly, whenever \(g^6 = 1\), this map \(f\) is an automorphism of the octonions:
$$ f(x+y) = f(x) + f(y) , \qquad f(x y) = f(x) f(y) \qquad \forall x,y \in \mathbb{O}. $$
and \(f\) has order 3:
$$ f(f(f(x))) = x \qquad \forall x \in \mathbb{O}. $$
To understand this latter fact, we can look at
Theorem 2.1 here implies that an octonion \(g\) with \({|g|} = 1\) defines an inner automorphism \(f \colon x \mapsto g x g^{-1}\) if and only if \(g\) has order 6.
However, the result is stated differently there. Paraphrasing somewhat, Lamont's theorem says that any \(g \in \mathbb{O}\) that is not a real multiple of \(1 \in \mathbb{O}\) defines an inner automorphism \(f \colon x \to g x g^{-1}\) if and only if \(g\) obeys
$$ 4 \mathrm{Re}(g)^2 = {|g|}^2. $$
This equation is equivalent to \(\mathrm{Re}(g) = \pm \frac{1}{2} {|g|}\), which is equivalent to \(g\) lying at either a \(60^\circ\) angle or a \(120^\circ\) angle from the octonion \(1\).
Nonzero octonions on the real line clearly define inner automorphisms. Thus, a nonzero octonion \(g\) defines an inner automorphism if and only if its angle from \(1\) is \(0^\circ, 60^\circ, 120^\circ\) or \(180^\circ\). In this case we can normalize \(g\) without changing the inner automorphism it defines, and then we have \(g^6 = 1\). Note also that \(g\) and \(-g\) define the same inner automorphism.
It follows that an octonion \(g\) on the unit sphere defines an inner automorphism iff \(g^6 = 1\), and that every nontrivial inner automorphism of \(\mathbb{O}\) has order 3.
However, if you look at Lamont's proof, you'll see the equation \(4 \text{Re}(g)^2 = {|g|}^2 \) plays no direct role! Instead, he really uses the assumption that \(g^3\) is a real multiple of \(1\), which is implied by this equation (as easily shown using what we've just seen).
From Lamont's work, one can see the Moufang identities and the characteristic equation for octonions are what force all inner automorphisms of the octonions to have order 3.
Thus, an argument giving a positive answer to my question might involve a link between triality and the Moufang identities. Conway and Smith seem to link them in On Quaternions and Octonions. But I haven't figured out how to get from the outer automorphisms of \(\text{Spin}(8)\) to the inner automorphisms of \(\mathbb{O}\), or vice versa!
September 16, 2025
I got some help from Vít Tuček on MathOverflow. He pointed out that Yokota gave a proof that all inner automorphisms of \(\mathbb{O}\) have order 3 using the Moufang identity and two ideas connected to triality. I'd like to spell it out here.
First, Yokota proves these:
Theorem 1.14.2. For any \(\alpha_3 \in \text{SO}(8)\) there are \(\alpha_1, \alpha_2 \in \text{SO}(8)\) such that
$$ \alpha_1(x) \, \alpha_2(y) = \alpha_3(x y). $$
for all \(x, y \in \mathbb{O}\). Moreover \(\alpha_1, \alpha_2\) are unique up to a common choice of sign.
Lemma 1.14.3. If \(\alpha_1, \alpha_2, \alpha_3 \in \text{SO}(8)\), then
$$ \alpha_1(x)\, \alpha_2(y) = \overline{\alpha_3(\overline{x y})}. $$
for all octonions \(x,y \in \mathbb{O}\) implies that
$$ \alpha_2(x)\, \alpha_3(y) = \overline{\alpha_1(\overline{x y})}. $$
for all \(x, y \in \mathbb{O}\).
He calls the theorem the "principle of triality for \(\text{SO}(8)\)". It's a step toward proving the fact that Spin(8) has an outer automorphism of order 3 relating its three 8-dimensional representations. He proves the lemma simply by equation-juggling using basic properties of normed division algebras.
Now suppose conjugation by \(g \in \mathbb{O}\) defines an inner automorphism of the octonions. We can normalize \(g \in \mathbb{O}\) without changing the inner automorphism it defines, and then we have \(g \overline{g} = 1\), so \(g^{-1} = \overline{g}\). Thus we have
$$ (g x \overline{g})(g y \overline{g}) = g (x y) \overline{g}. $$
Next we use a cool fact about the octonions called the Moufang identity:
$$ (b c)(d b) = b(c d)b $$
where the right-hand side is actually well-defined regardless of how you parenthesize it. Take \(b = \overline{g}\) and get
$$ (\overline{g} c)(d \overline{g}) = \overline{g}(c d) \overline{g}. $$
We can rewrite this equation if we take
$$ \alpha_1(x) = \overline{g} x , \; \alpha_2(x) = x \overline{g} , \; \alpha_3(x) = g x g. $$
Namely, we can rewrite it as
$$ \alpha_1(c) \, \alpha_2(d) = \overline{\alpha_3(\overline{c d})}. $$
Since \(\alpha_1, \alpha_2, \alpha_3 \in \text{SO}(8)\), Lemma 1.14.3 jumps in and tells us
$$ \alpha_2(c)\, \alpha_3(d) = \overline{\alpha_1(\overline{c d})}. $$
Concretely this means
$$ (c \overline g)(g d g) = \overline{\overline{g} (\overline{c d})} $$
or in other words
$$ (c \overline g)(g d g) = (c d) g. $$
Now, cleverly taking \(c = g x\), \(d = y g\), we get
$$ (g x \overline{g})(g y g^2) = g (x y) g^2. $$
But remember we have assumed that conjugation by \(g\) is an inner automorphism and \(g^{-1} = \overline{g}\). This gives a very similar equation:
$$ (g x \overline{g})(g y \overline{g}) = g (x y) \overline{g}. $$
Then the uniqueness part of Theorem 1.14.2 implies we must have
$$ \overline{g} = \pm g^2 $$
or
$$ g^3 = \pm 1 $$
so \(g^6 = 1\) and \(g\) defines an inner automorphism of order 3.
This argument is pretty convoluted, so it's hard to see how the threeness of triality forces inner automorphisms of the octonions to have order 3. However, we can also turn this argument around and show that \(g^6 = 1\) implies that \(g\) defines an inner automorphism.
September 17, 2025
This week, scientists are meeting in Manchester to discuss rules on studying 'mirror-image biology'. That includes biomolecules that are mirror images of the usual ones — and maybe someday organisms made from those mirror image molecules!
Mirror-image glucose tastes as sweet as the usual stuff, but provides no calories because we can't metabolize it. Dozens of research groups have been synthesizing mirror-image proteins, DNA and RNA for three decades. Mirror-image DNA can hold information just like ordinary DNA — but it's more resistant to biodegradation, and easier to distinguish from contaminating natural DNA.
In 2019, the NSF gave out some grants to develop a mirror cell. Some of the researchers later decided it was a bad idea and quit. Mirror-image organisms might be dangerous.
Or they might just starve to death.
For more, see:
Wow! The black hole at the center of a nearby galaxy is incredibly dynamic!
In 2017, the magnetic fields near its event horizon were spiraling around one way. By 2018 they settled down. But by 2021, they were spiraling in the opposite direction!
This black hole is incredibly massive: about 6 billion times heavier than our Sun. But it radius is only 120 times the distance between the Sun and the Earth. That's big, but it doesn't take light very long to go that far: just 16 hours. So it's theoretically possible for magnetic fields to change quite fast.
But what's making these magnetic fields? It's hot ionized gas called plasma, spiraling down into the black hole like water going down the drain of your bathtub.... if your bathtub was huge and full of plasma. Did the swirling motion of this stuff change significantly in just a few years? Or just the magnetic fields?
This black hole is called M87* since it's in the middle of a galaxy called M87, which is 55 million light years away. For comparison the Milky Way is 90 thousand light years across, and Andromeda is 2.5 million light years away. But M87 still counts as "close" because its redshift is tiny. The Universe is really big.
Anyway, the cool part here is that we're starting to see the dynamics of magnetic fields near a supermassive black hole. It's like black holes have "weather'. As usual, things are more interesting than the simple theoretical models we had before we saw what's actually going on. Imagine trying to understand weather before you looked at it.
Fall is in the air here in Edinburgh! The daylight is shrinking fast, and the sun is sinking toward the horizon. At the height of summer we had an astounding 17½ hours of sunlight... but by the winter solstice that will shrink to a measly 7. That's the price of living at a northern latitude. Look at the shortest days:
London: 7 hours and 50 minutes
Edinburgh: 6 hours and 57 minutes
Orkney: 6 hours and 10 minutes
Shetland: 5 hours and 49 minutes
In the depths of winter you lose almost an hour of sun as you go from London to Edinburgh, and another as you go up to the Shetland Islands. You can see why people fall in love with those islands in the summer, buy a place there, and then can't stand the winter! It's not just cold, it's dark.
The graph is from here:
If spacetime had far more points than it does in our universe, then the way we do logic and math might be very different.
In our universe, most mathematicians act like we can write down infinitely many different strings of symbols. But this is just the smallest infinity, called\(\aleph_0\).. There are a lot more real numbers, namely \(2^{\aleph_0}\).. This larger infinity sets the limits on how many points there are in space. But since there's a limitation to the accuracy of our measurements, we can write down at most \(\aleph_0\) different symbol strings. In our universe.
There are much larger infinities, though. Logicians have thought about logic with infinitely long statements — even for one of these much larger infinities. It's called 'infinitary logic'. We can't really use infinitary logic, but we can prove theorems about what it would be like.
I don't know if physicists have imagined laws of physics that would give spacetimes with 'more points per volume', whose inhabitants could actually use infinitary logic. For example, imagine a universe whose inhabitants use an alphabet with \(2^{\aleph_0}\) different symbols — and can actually recognize the difference between them! They could talk about vastly more complex things than we can. Their math would be much deeper. \(\aleph_0\) would seem small to them.
I think someone should think hard about this, just for fun. It could at least make for a good science fiction story.
Here's an easy intro to infinitary logic:
Here's a deeper intro:
I think mathematics would at least be thought about very differently in a universe where you could write infinitely long strings. First order logic as we know it and finite/recursive axiomatizations would be much less important than they are to mathematicians in our universe, and a theory like ZFC would probably be considered a super weak foundation.Ordinary first-order logic is 'compact'. This means that if you have a theory in first-order logic with infinitely many axioms, and every finite subset of these axioms has a model, then the whole set of axioms has a model. This is extremely important in logic, and it connects logic to topology:
If you give me a cardinal \(\kappa\), we can talk about a logic that allows infinitely many variable names, infinitely long conjunctions, and formulae with infinitely many alternating quantifiers \(\forall\exists\forall\)... — but only if these infinities are less than \(\kappa\). This logic is called \(L(\kappa,\kappa)\).
Then we say \(\kappa\) is strongly compact if whenever you have a theory in this logic with infinitely many axioms, and every subset of axioms with cardinality \( \lt \kappa\) has a model, the whole theory has a model.
Logicians would probably enjoy living in a universe where people used the logic \(L(\kappa,\kappa)\) for a strongly compact cardinal \(\kappa\). But it turns out strongly compact cardinals bigger than \(\aleph_0\) have to be really, really, really, really, really large. For example any strongly compact cardinal is measurable.
September 26, 2025
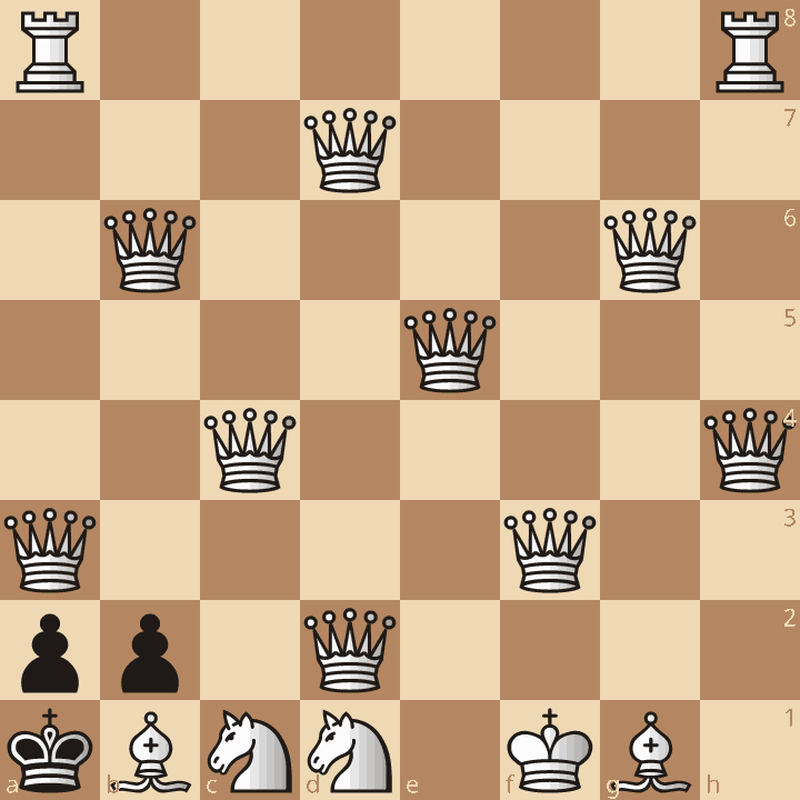
When playing chess, it's impossible to get into a position where you have more than 218 different moves you can make. This has long been suspected, but apparently it's now been proved!
It was not proved by checking all \(8.7 \times 10^{45}\) reachable chess positions. Instead, someone known to me only as Tobs45 seems to have figured out a better proof:
The above theoretically reachable • yet utterly insane • position with 218 moves for White was published by Nenad Petrović in 1964. Note that white has 9 queens, the most possible. Reading around, I found someone saying "it is very rare to see a player with 9 queens in actual games." I find that pretty amusing, like "it is very rare to see people with more than 2 heads".
Here's the position with the most moves, even though it's not reachable because it violates the rules of chess. White has the most 288 moves here, since there are 6 × 6 open squares, each of which is under attack by 8 queens, for a total of 36 × 8 = 288 possibilities.

Since I'm a mathematician, some people think I should be good at chess. In fact I don't play chess and don't know much about it. Don't be fooled by this post: this stuff just caught my eye.
I had to suffer through grad school watching my friends play chess at Ashdown House, the grad student dorm at MIT, every Thursday night. That was the night where they gave us free cake. I wanted to talk about math and physics and music and life, not play chess!
When I was a kid, I decided I didn't like games very much, because I hated to lose, yet didn't want to waste a lot of time getting good at games. I saved my energy for the Great Game. No, not taking over central Asian countries: mathematics.
I've never quite figured out whether this is a serious personality flaw. There are just too many interesting things to learn for me to spend time on games.
September 30, 2025
'Prussian blue' is a crystal so blue you can't accurately show it on most computer screens, since they can only display a limited region of color space. Its structure is really cool. It's a cubical lattice made of iron atoms, each surrounded by 6 cyanides — carbon and nitrogen.
But let Sean Silver explain it:
The modern way of manufacturing the pigment involves synthesizing it directly from some form of hexacyanoferrate; hexacyanoferrate is one iron atom bound with six cyanide molecules radiating equidistantly from it, like the tiny metal doodads scooped up in the children’s game called “jacks.” These are snapped into a theoretically endless lattice, the point of each hexacynoferrate compound lining up with a point of another, which are locked into place by iron ions with a different charge. So: if we were to describe what we saw along any single axis, we would see iron(II), cyanide, iron(III), cyanide, iron(II), and so on.This is from here:
Neither of the precursors to Prussian Blue is blue. And, though the very word "cyanide" comes from the Greek word meaning "blue," this proves to be a backformation from Prussian Blue; in roughly 1750, cyanide was isolated as its own (deadly) compound by cracking it out of the pigment, and named "blue" despite the fact that it is nearly colorless. Hexacyanoferrate therefore has the very word "blue" in its name, though, by itself, it is hardly blue at all.
Understanding the color of Prussian Blue requires a short detour. I have become interested, lately, in situations where a whole is different from the sum of its parts — and that is the case with Prussian Blue, where blueness is an emergent effect of combination.
The iron in Prussian Blue is in two different oxidation states — which is to say, has two different numbers of electrons. As iron(II), it has given up two electrons, and is a dark brown color. Iron(III) [where it's given up 3 electrons] is rust-red, precisely because rust is mostly composed of iron in that third oxidation state.This picture shows how intervalence charge transfer works:The ability of iron easily to switch between oxidation states happens to be what makes it crucial to blood — and makes blood visibly different when oxygenated. When the iron(II) in hemoglobin forms a bond with oxygen, it gives up an electron to become iron(III); it changes its oxidation state, and becomes bright red. That same compound will later give up its oxygen to a cell which needs it, reclaiming its electron and reverting to duller, darker color gained from iron(II).
The blueness only happens when both ions are locked in close proximity, from a special process called intervalence charge transfer. When hit with light of the right wavelength, some of the iron(II) ions throw off an electron, which is captured by a neighboring iron(III). Though the individual atoms stay locked in the lattice, the ions switch places, one shedding an electron, which the other gains. Because the compound absorbs only the precise orange wavelength that triggers the charge transfer, it reflects everything else. In white light, our eyes register the sum of the reflection as blue.
Here's Prussian blue in all its crystalline glory!
Iron(III) is red.
The red balls sit at every other vertex in a cubic lattice. What do you call that pattern? I forget!
The yellow balls also sit at every other vertex of the cubic lattice. Along each edge there's a blue ball and a red ball.
You can rotate this image and play around with it in other ways at ChemTube 3D:
Roughly.
But nothing is ever quite so simple! This gives more details:
The Fe(II) centers, which are low spin, are surrounded by six carbon ligands in an octahedral configuration. The Fe(III) centers, which are high spin, are octahedrally surrounded on average by 4.5 nitrogen atoms and 1.5 oxygen atoms (the oxygen from the six coordinated water molecules). Around eight (interstitial) water molecules are present in the unit cell, either as isolated molecules or hydrogen bonded to the coordinated water. It is worth noting that in soluble hexacyanoferrates Fe(II or III) is always coordinated to the carbon atom of a cyanide, whereas in crystalline Prussian blue Fe ions are coordinated to both C and N.'Ligand' basically just means the carbons are linked to the iron. When a bunch of ions or molecules link to a metal atom, we call them 'ligands' and call the resulting structure a 'coordination complex'.
I want to learn more about coordination complexes!