Errata in Bull. Amer. Math. Soc. 42 (2005), 213.
Also available in Postscript and PDF.
The octonions are the largest of the four normed division algebras. While somewhat neglected due to their nonassociativity, they stand at the crossroads of many interesting fields of mathematics. Here we describe them and their relation to Clifford algebras and spinors, Bott periodicity, projective and Lorentzian geometry, Jordan algebras, and the exceptional Lie groups. We also touch upon their applications in quantum logic, special relativity and supersymmetry.
For a lighter approach, try this two-part feature in Plus Magazine:
and in which Helen Joyce and I have a fun nontechnical chat about the real numbers, complex numbers, quaternions and octonions. Also try this article John Huerta and I wrote for Scientific American:
John Huerta and I have written a number of technical papers about the octonions and other normed division algebras in physics:
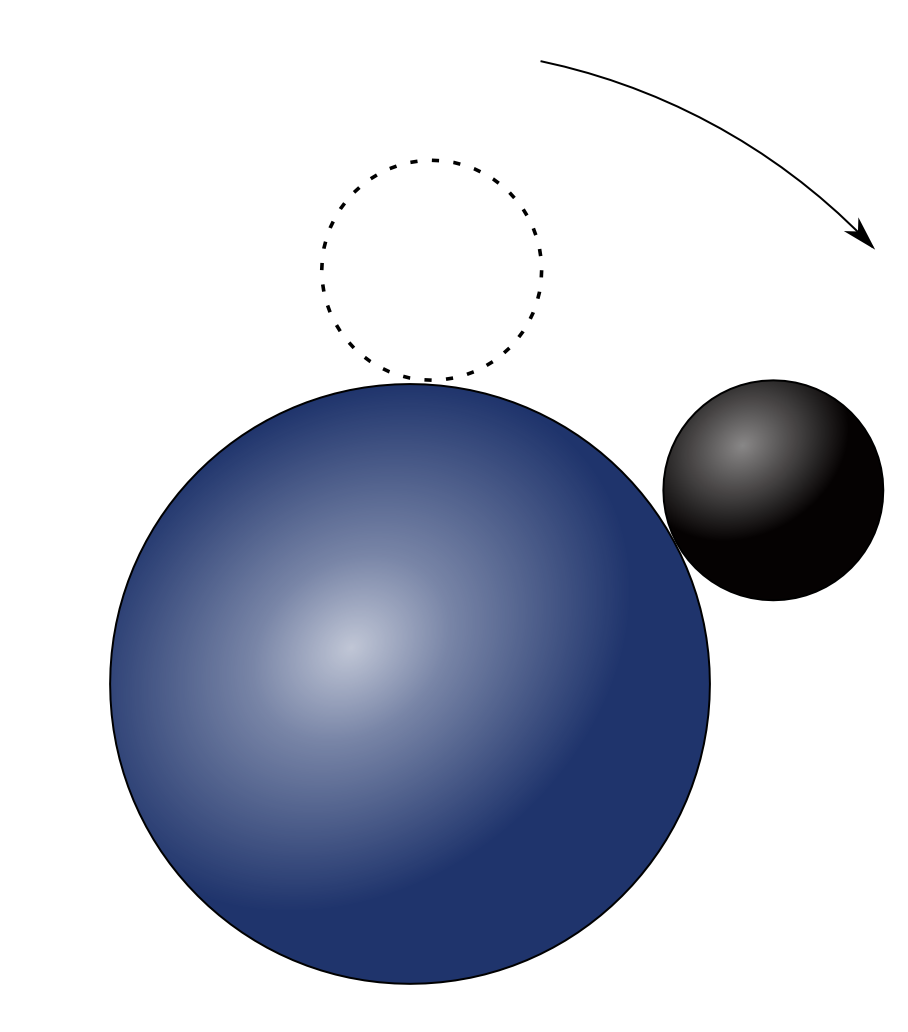
Huerta and I have also written about a curious connection between octonions, the exceptional group G2 and a ball rolling on another ball 3 times as big:
In the broad light of day mathematicians check their equations and their proofs, leaving no stone unturned in their search for rigour. But, at night, under the full moon, they dream, they float among the stars and wonder at the miracle of the heavens. They are inspired. Without dreams there is no art, no mathematics, no life. - Michael Atiyah
© 2023 John Baez
baez@math.removethis.ucr.andthis.edu