4.2 $\F _4$

The second smallest of the exceptional Lie groups is the 52-dimensional group $\F _4$. The geometric meaning of this group became clear in a number of nearly simultaneous papers by various mathematicians. In 1949, Jordan constructed the octonionic projective plane using projections in $\h _3(\O)$. One year later, Armand Borel [8] noted that $\F _4$ is the isometry group of a 16-dimensional projective plane. In fact, this plane is none other than than $\OP^2$. Also in 1950, Claude Chevalley and Richard Schafer [18] showed that $\F _4$ is the automorphism group of $\h _3(\O)$. In 1951, Freudenthal [35] embarked upon a long series of papers in which he described not only $\F _4$ but also the other exceptional Lie groups using octonionic projective geometry. To survey these developments, one still cannot do better than to read his classic 1964 paper on Lie groups and the foundations of geometry [38].

Let us take Chevalley and Schafer's result as the definition of $\F _4$:

$$\F _4 = \Aut (\h _3(\O)) .$$

Its Lie algebra is thus

$$\f _4 = \Der (\h _3(\O)).$$

As we saw in Section 3.4, points of $\OP^2$ correspond to trace-1 projections in the exceptional Jordan algebra. It follows that $\F _4$ acts as transformations of $\OP^2$. In fact, we can equip $\OP^2$ with a Riemannian metric for which $\F _4$ is the isometry group. To get a sense of how this works, let us describe $\OP^2$ as a quotient space of $\F _4$.

In Section 3.4 we saw that the exceptional Jordan algebra can be built using natural operations on the scalar, vector and spinor representations of $\Spin (9)$. This implies that $\Spin (9)$ is a subgroup of $\F _4$. Equation (3.4) makes it clear that $\Spin (9)$ is precisely the subgroup fixing the element

$$% latex2html id marker 1684 \left( \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right).$$

Since this element is a trace-one projection, it corresponds to a point of $\OP^2$. We have already seen that $\F _4$ acts transitively on $\OP^2$. It follows that

$$\OP^2 \iso \F _4 /\Spin (9) .$$

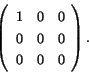
This fact has various nice spinoffs. First, it gives an easy way to compute the dimension of $\F _4$:

$$\dim(\F _4) = \dim(\Spin (9)) + \dim(\OP^2) = 36 + 16 = 52.$$

Second, since $\F _4$ is compact, we can take any Riemannian metric on $\OP^2$ and average it with respect to the action of this group. The isometry group of the resulting metric will automatically include $\F _4$ as a subgroup. With more work [5], one can show that actually

$$\F _4 = \Isom (\OP^2)$$

and thus

$$\f _4 = \isom (\OP^2).$$

Equation (4.2) also implies that the tangent space of our chosen point in $\OP^2$ is isomorphic to $\f _4/\so (9)$. But we already know that this tangent space is just $\O^2$, or in other words, the spinor representation of $\so (9)$. We thus have

$$\f _4 \iso \so (9) \oplus S_9$$

as vector spaces, where $\so (9)$ is a Lie subalgebra. The bracket in $\f _4$ is built from the bracket in $\so (9)$, the action $\so (9) \tensor S_9 \to S_9$, and the map $S_9 \tensor S_9 \to \so (9)$ obtained by dualizing this action. We can also rewrite this description of $\f _4$ in terms of the octonions, as follows:

$$\f _4 \iso \so (\O \oplus \R) \oplus \O^2$$

This last formula suggests that we decompose $\f _4$ further using the splitting of $\O \oplus \R$ into $\O$ and $\R$. It is easily seen by looking at matrices that for all $n,m$ we have

$$% latex2html id marker 1691\so (n+m) \iso \so (n) \oplus \so (m) \, \oplus\, V_n \tensor V_m.$$

Moreover, when we restrict the representation $S_9$ to $\so (8)$, it splits as a direct sum $S_8^+ \oplus S_8^-$. Using these facts and equation (4.2), we see

$$\f _4 \iso \so (8) \oplus V_8 \oplus S_8^+ \oplus S_8^-$$

This formula emphasizes the close relation between $\f _4$ and triality: the Lie bracket in $\f _4$ is completely built out of maps involving $\so (8)$ and its three 8-dimensional irreducible representations! We can rewrite this in a way that brings out the role of the octonions:

$$\f _4 \iso \so (\O) \oplus \O^3$$

While elegant, none of these descriptions of $\f _4$ gives a convenient picture of all the derivations of the exceptional Jordan algebra. In fact, there is a nice picture of this sort for $\h _3(\K)$ whenever $\K$ is a normed division algebra. One way to get a derivation of the Jordan algebra $\h _3(\K)$ is to take a derivation of $\K$ and let it act on each entry of the matrices in $\h _3(\K)$. Another way uses elements of

$$% latex2html id marker 1694 \sa _3(\K) = \{ x \in \K[3] \colon \; x^* = -x,\; \tr (x) = 0 \} .$$

Given $x \in \sa _3(\K)$, there is a derivation $\ad _x$ of $\h _3(\K)$ given by

$$\ad _x (a) = [x,a] .$$

In fact [4], every derivation of $\h _3(\K)$ can be uniquely expressed as a linear combination of derivations of these two sorts, so we have

$$\Der (\h _3(\K)) \iso \Der (\K) \oplus \sa _3(\K)$$

as vector spaces. In the case of the octonions, this decomposition says that

$$\f _4 \iso \g _2 \oplus \sa _3(\O) .$$

In equation (4.2), the subspace $\Der (\K)$ is always a Lie subalgebra, but $\sa _3(\K)$ is not unless $\K$ is commutative and associative — in which case $\Der (\K)$ vanishes. Nonetheless, there is a formula for the brackets in $\Der (\h _3(\K))$ which applies in every case [70]. Given $D,D' \in \Der (\K)$ and $x,y \in \sa _3(\K)$, we have

$$\begin{array}{lcl} [D,D'] &=& DD' - D'D \cr [D,\ad _x] &=&... ...yle{{1\over 3} \sum_{i,j = 1}^3 D_{x_{ij},y_{ij}} } \end{array}$$

where $D$ acts on $x$ componentwise, $[x,y]_0$ is the trace-free part of the commutator $[x,y]$, and $D_{x_{ij},y_{ij}}$ is the derivation of $\K$ defined using equation (4.1).

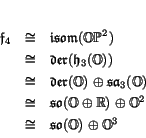
Summarizing these different descriptions of $\f _4$, we have:

Theorem 5.   The compact real form of $\f _4$ is given by

$$% latex2html id marker 1699 \begin{array}{lcl} \f _4 &\is... ...s \R) \oplus \O^2 \\ &\iso & \so (\O) \oplus \O^3 \end{array}$$

where in each case the Lie bracket is built from natural bilinear operations on the summands.

home