A one-dimensional projective space is called a projective line. Projective lines are not very interesting from the viewpoint of axiomatic projective geometry, since they have only one line on which all the points lie. Nonetheless, they can be geometrically and topologically interesting. This is especially true of the octonionic projective line. As we shall see, this space has a deep connection to Bott periodicity, and also to the Lorentzian geometry of 10-dimensional spacetime.
Suppose ![]() is a normed division algebra. We have already defined
is a normed division algebra. We have already defined
![]() when
when ![]() is associative, but this definition does not work well
for the octonions: it is wiser to take a detour through Jordan
algebras. Let
is associative, but this definition does not work well
for the octonions: it is wiser to take a detour through Jordan
algebras. Let ![]() be the space of
be the space of ![]() hermitian
matrices with entries in
hermitian
matrices with entries in ![]() . It is easy to check that this becomes a
Jordan algebra with the product
. It is easy to check that this becomes a
Jordan algebra with the product
![]() . We
can try to build a projective space from this Jordan algebra using the
construction in the previous section. To see if this
succeeds, we need to ponder the projections in
. We
can try to build a projective space from this Jordan algebra using the
construction in the previous section. To see if this
succeeds, we need to ponder the projections in ![]() . A little
calculation shows that besides the trivial projections 0 and 1, they
are all of the form
. A little
calculation shows that besides the trivial projections 0 and 1, they
are all of the form
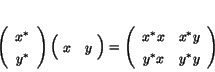
Given any nonzero element
![]() , we can normalize it and then
use the above formula to get a point in
, we can normalize it and then
use the above formula to get a point in ![]() , which we call
, which we call
![]() . This allows us to describe
. This allows us to describe ![]() in terms
of lines through the origin, as follows. Define an equivalence relation
on nonzero elements of
in terms
of lines through the origin, as follows. Define an equivalence relation
on nonzero elements of ![]() by
by
Be careful: when ![]() is the octonions, the line through the
origin containing
is the octonions, the line through the
origin containing ![]() is not always equal to
is not always equal to
We can make ![]() into a manifold as follows. By the above
observations, we can cover it with two coordinate charts: one containing
all points of the form
into a manifold as follows. By the above
observations, we can cover it with two coordinate charts: one containing
all points of the form ![]() , the other containing all points of the
form
, the other containing all points of the
form ![]() . It is easy to check that
. It is easy to check that
![]() iff
iff ![]() , so the transition function from the first chart to the second
is the map
, so the transition function from the first chart to the second
is the map
![]() . Since this transition function and its
inverse are smooth on the intersection of the two charts,
. Since this transition function and its
inverse are smooth on the intersection of the two charts, ![]() becomes a smooth manifold.
becomes a smooth manifold.
When pondering the geometry of projective lines it is handy to
visualize the complex case, since ![]() is just the familiar
'Riemann sphere'. In this case, the map
is just the familiar
'Riemann sphere'. In this case, the map
where we choose the sphere to have diameter 1. This map from ![]() to
to
![]() is one-to-one and almost onto, missing only the point at
infinity, or 'north pole'. Similarly, the map
is one-to-one and almost onto, missing only the point at
infinity, or 'north pole'. Similarly, the map
All these ideas painlessly generalize to ![]() for any normed division
algebra
for any normed division
algebra ![]() . First of all, as a smooth manifold
. First of all, as a smooth manifold ![]() is just a
sphere with dimension equal to that of
is just a
sphere with dimension equal to that of ![]() :
:
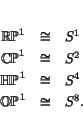
One of the nice things about ![]() is that it comes equipped with a
vector bundle whose fiber over the point
is that it comes equipped with a
vector bundle whose fiber over the point ![]() is the line
through the origin corresponding to this point. This bundle is called
the canonical line bundle,
is the line
through the origin corresponding to this point. This bundle is called
the canonical line bundle, ![]() . Of course, when we are working
with a particular division algebra, 'line' means a copy of this division
algebra, so if we think of them as real vector bundles,
. Of course, when we are working
with a particular division algebra, 'line' means a copy of this division
algebra, so if we think of them as real vector bundles,
![]() and
and ![]() have dimensions 1,2,4, and 8, respectively.
have dimensions 1,2,4, and 8, respectively.
These bundles play an important role in topology, so it is good to
understand them in a number of ways. In general, any ![]() -dimensional
real vector bundle over
-dimensional
real vector bundle over ![]() can be formed by taking trivial bundles
over the northern and southern hemispheres and gluing them together
along the equator via a map
can be formed by taking trivial bundles
over the northern and southern hemispheres and gluing them together
along the equator via a map
![]() . We must
therefore be able to build the canonical line bundles
. We must
therefore be able to build the canonical line bundles
![]() and
and ![]() using maps
using maps
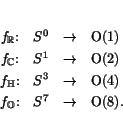
The importance of the map ![]() becomes clearest if we form the
inductive limit of the groups
becomes clearest if we form the
inductive limit of the groups ![]() using the obvious inclusions
using the obvious inclusions
![]() , obtaining a topological group
called
, obtaining a topological group
called ![]() . Since
. Since ![]() is included in
is included in ![]() ,
we can think of
,
we can think of ![]() as a map from
as a map from ![]() to
to ![]() .
Its homotopy class
.
Its homotopy class ![]() has the following marvelous property,
mentioned in the Introduction:
has the following marvelous property,
mentioned in the Introduction:
Another nice perspective on the canonical line bundles ![]() comes from
looking at their unit sphere bundles. Any fiber of
comes from
looking at their unit sphere bundles. Any fiber of ![]() is naturally
an inner product space, since it is a line through the origin in
is naturally
an inner product space, since it is a line through the origin in ![]() .
If we take the unit sphere in each fiber, we get a bundle of
.
If we take the unit sphere in each fiber, we get a bundle of
![]() -spheres over
-spheres over ![]() called the Hopf bundle:
called the Hopf bundle:
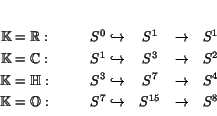
We can understand the Hopf maps better by thinking about inverse images
of points. The inverse image ![]() of any point
of any point ![]() is a
is a ![]() -sphere in
-sphere in ![]() , and the inverse image of any pair of
distinct points is a pair of linked spheres of this sort. When
, and the inverse image of any pair of
distinct points is a pair of linked spheres of this sort. When ![]() we get linked circles in
we get linked circles in ![]() , which form the famous Hopf link:
, which form the famous Hopf link:
When ![]() , we get a pair of linked 7-spheres in
, we get a pair of linked 7-spheres in ![]() .
.
To quantify this notion of linking, we can use the 'Hopf invariant'.
Suppose for a moment that ![]() is any natural number greater than one,
and let
is any natural number greater than one,
and let
![]() be any smooth map. If
be any smooth map. If ![]() is
the normalized volume form on
is
the normalized volume form on ![]() , then
, then ![]() is a closed
is a closed
![]() -form on
-form on ![]() . Since the
. Since the ![]() th cohomology of
th cohomology of ![]() vanishes,
vanishes,
![]() for some
for some ![]() -form
-form ![]() .
We define the Hopf invariant of
.
We define the Hopf invariant of ![]() to be the number
to be the number
To see how the Hopf invariant is related to linking, we can compute it
using homology rather than cohomology. If we take any two regular
values of ![]() , say
, say ![]() and
and ![]() , the inverse images of these points are
compact oriented
, the inverse images of these points are
compact oriented ![]() -dimensional submanifolds of
-dimensional submanifolds of ![]() . We
can always find an oriented
. We
can always find an oriented ![]() -dimensional submanifold
-dimensional submanifold
![]() that has boundary equal to
that has boundary equal to ![]() and that intersects
and that intersects
![]() transversely. The dimensions of
transversely. The dimensions of ![]() and
and ![]() add up
to
add up
to ![]() , so their intersection number is well-defined. By the
duality between homology and cohomology, this number equals the Hopf
invariant
, so their intersection number is well-defined. By the
duality between homology and cohomology, this number equals the Hopf
invariant ![]() . This shows that the Hopf invariant is an integer.
Moreover, it shows that when the Hopf invariant is nonzero, the inverse
images of
. This shows that the Hopf invariant is an integer.
Moreover, it shows that when the Hopf invariant is nonzero, the inverse
images of ![]() and
and ![]() are linked.
are linked.
Using either of these approaches we can compute the Hopf invariant of
![]() ,
, ![]() and
and ![]() . They all turn out to have Hopf invariant 1.
This implies, for example, that the inverse images of distinct points
under
. They all turn out to have Hopf invariant 1.
This implies, for example, that the inverse images of distinct points
under ![]() are nontrivially linked 7-spheres in
are nontrivially linked 7-spheres in ![]() . It
also implies that
. It
also implies that ![]() ,
, ![]() and
and ![]() give nontrivial elements of
give nontrivial elements of
![]() for
for ![]() , and
, and ![]() .
In fact, these elements
generate the torsion-free part of
.
In fact, these elements
generate the torsion-free part of
![]() .
.
A deep study of the Hopf invariant is one way to prove that any division
algebra must have dimension 1, 2, 4 or 8. One can show that if there
exists an ![]() -dimensional division algebra, then
-dimensional division algebra, then ![]() must be parallelizable: it must admit
must be parallelizable: it must admit ![]() pointwise linearly independent
smooth vector fields. One can also show that for
pointwise linearly independent
smooth vector fields. One can also show that for ![]() ,
, ![]() is
parallelizable iff there exists a map
is
parallelizable iff there exists a map
![]() with
with
![]() . The hard part is the final step: showing that a map from
. The hard part is the final step: showing that a map from
![]() to
to ![]() can have Hopf invariant 1 only if
can have Hopf invariant 1 only if ![]() , or
, or
![]() . Proving this requires algebraic topology that goes far beyond the
scope of this paper [2,9,52]. There is just one thing we
wish to note about this proof: it involves Bott periodicity, which we
describe in the next section. As we shall see, Bott periodicity has a
natural explanation in terms of the canonical line bundle over
. Proving this requires algebraic topology that goes far beyond the
scope of this paper [2,9,52]. There is just one thing we
wish to note about this proof: it involves Bott periodicity, which we
describe in the next section. As we shall see, Bott periodicity has a
natural explanation in terms of the canonical line bundle over ![]() .
There is thus a sense in which the existence of the octonions is
'responsible' for the nonexistence of division algebras in dimensions
other than 1, 2, 4, and 8!
.
There is thus a sense in which the existence of the octonions is
'responsible' for the nonexistence of division algebras in dimensions
other than 1, 2, 4, and 8!
© 2001 John Baez