3.3
In Section 3.1 we sketched a systematic approach to projective
lines over the normed division algebras. The most famous example is the
Riemann sphere, ![]() . As emphasized by Penrose [72], this space
has a fascinating connection to Lorentzian geometry -- or in other words,
special relativity. All conformal transformations of the Riemann
sphere come from fractional linear transformations
. As emphasized by Penrose [72], this space
has a fascinating connection to Lorentzian geometry -- or in other words,
special relativity. All conformal transformations of the Riemann
sphere come from fractional linear transformations
In fact, these results are not special to the complex case: the same
ideas work for the other normed division algebras as well! The algebras
![]() and
and ![]() are related to Lorentzian geometry in 3, 4, 6, and
10 dimensions, respectively [63,64,65,78,86]. Even
better, a full explanation of this fact brings out new relationships
between the normed division algebras and spinors. In what follows we
explain how this works for all 4 normed division algebras, with special
attention to the peculiarities of the octonionic case.
are related to Lorentzian geometry in 3, 4, 6, and
10 dimensions, respectively [63,64,65,78,86]. Even
better, a full explanation of this fact brings out new relationships
between the normed division algebras and spinors. In what follows we
explain how this works for all 4 normed division algebras, with special
attention to the peculiarities of the octonionic case.
To set the stage, we first recall the most mysterious of the four
infinite series of Jordan algebras listed at the beginning of Section
3: the spin factors. We described these quite concretely, but
a more abstract approach brings out their kinship to Clifford algebras.
Given an ![]() -dimensional real inner product space
-dimensional real inner product space ![]() , let the spin
factor
, let the spin
factor ![]() be the Jordan algebra freely generated by
be the Jordan algebra freely generated by ![]() modulo
relations
modulo
relations
Though Jordan algebras were invented to study quantum mechanics, the
spin factors are also deeply related to special relativity. We can
think of
![]() as Minkowksi spacetime, with
as Minkowksi spacetime, with
![]() as space and
as space and ![]() as time. The reason is that
as time. The reason is that ![]() is naturally
equipped with a symmetric bilinear form of signature
is naturally
equipped with a symmetric bilinear form of signature ![]() , the Minkowski metric:
, the Minkowski metric:
When ![]() is at least 2-dimensional, we can build a projective space from
the Jordan algebra
is at least 2-dimensional, we can build a projective space from
the Jordan algebra ![]() . The result is none other than the heavenly
sphere! To see this, note that aside from the elements 0 and 1, all
projections in
. The result is none other than the heavenly
sphere! To see this, note that aside from the elements 0 and 1, all
projections in ![]() are of the form
are of the form
![]() where
where ![]() has norm one. These are the points of our projective
space, but as we have seen, they also correspond to points of the
heavenly sphere. Our projective space has just one line, corresponding
to the projection
has norm one. These are the points of our projective
space, but as we have seen, they also correspond to points of the
heavenly sphere. Our projective space has just one line, corresponding
to the projection ![]() . We can visualize this line as the
heavenly sphere itself.
. We can visualize this line as the
heavenly sphere itself.
What does all this have to do with normed division algebras? To answer
this, let ![]() be a normed division algebra of dimension
be a normed division algebra of dimension ![]() . Then
the Jordan algebra
. Then
the Jordan algebra ![]() is secretly a spin factor! There is an
isomorphism
is secretly a spin factor! There is an
isomorphism
These facts have a number of nice consequences. First of all, since the
Jordan algebras
![]() and
and ![]() are isomorphic, so are
their associated projective spaces. We have seen that the former space
is the heavenly sphere
are isomorphic, so are
their associated projective spaces. We have seen that the former space
is the heavenly sphere
![]() , and that the latter is
, and that the latter is
![]() . It follows that
. It follows that
Secondly, it follows that the determinant-preserving linear
transformations of ![]() form a group isomorphic to
form a group isomorphic to ![]() .
How can we find some transformations of this sort? If
.
How can we find some transformations of this sort? If ![]() , this
is easy: when
, this
is easy: when
![]() and
and
![]() , we again have
, we again have
![]() , and
, and
For the other two normed division algebras the above calculation
involving determinants breaks down, and it even becomes tricky to define
the group ![]() , so we start by working at the Lie algebra level.
We say a
, so we start by working at the Lie algebra level.
We say a ![]() matrix with entries in the normed division algebra
matrix with entries in the normed division algebra
![]() is traceless if the sum of its diagonal entries is zero. Any
such traceless matrix acts as a real-linear operator on
is traceless if the sum of its diagonal entries is zero. Any
such traceless matrix acts as a real-linear operator on ![]() . When
. When
![]() is commutative and associative, the space of operators coming from
is commutative and associative, the space of operators coming from
![]() traceless matrices with entries in
traceless matrices with entries in ![]() is closed under
commutators, but otherwise it is not, so we define
is closed under
commutators, but otherwise it is not, so we define ![]() to be the
Lie algebra of operators on
to be the
Lie algebra of operators on ![]() generated by operators of this
form. This Lie algebra in turn generates a Lie group of real-linear
operators on
generated by operators of this
form. This Lie algebra in turn generates a Lie group of real-linear
operators on ![]() , which we call
, which we call ![]() . Note that
multiplication in this group is given by composition of real-linear
operators, which is associative even for
. Note that
multiplication in this group is given by composition of real-linear
operators, which is associative even for ![]() .
.
The Lie algebra ![]() comes born with a representation:
its fundamental representation as real-linear operators on
comes born with a representation:
its fundamental representation as real-linear operators on ![]() ,
given by
,
given by
Now let us return to the case ![]() . One can prove that the
representation of
. One can prove that the
representation of ![]() on
on ![]() is determinant-preserving
simply by checking that
is determinant-preserving
simply by checking that

We conclude with some words about how all this relates to spinors. The
machinery of Clifford algebras and spinors extends effortlessly from the
case of inner product spaces to vector spaces equipped with an
indefinite metric. In particular, the Lorentz group ![]() has
a double cover called
has
a double cover called ![]() , and this group has certain
representations called spinor representations. When
, and this group has certain
representations called spinor representations. When ![]() or
or ![]() ,
we actually have
,
we actually have
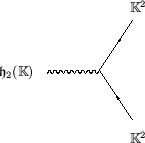
In the case ![]() , Penrose [72] has described a nice trick for
getting points on the heavenly sphere from spinors.
In fact, it also works for other normed division algebras:
if
, Penrose [72] has described a nice trick for
getting points on the heavenly sphere from spinors.
In fact, it also works for other normed division algebras:
if
![]() is nonzero, the hermitian matrix
is nonzero, the hermitian matrix
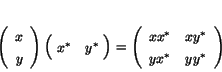
© 2001 John Baez