4.4
We begin with the 78-dimensional exceptional Lie group ![]() .
As we mentioned in Section 3.4, there is a nice description of a
certain noncompact real form of
.
As we mentioned in Section 3.4, there is a nice description of a
certain noncompact real form of ![]() as the group of collineations
of
as the group of collineations
of ![]() , or equivalently, the group of determinant-preserving
linear transformations of
, or equivalently, the group of determinant-preserving
linear transformations of ![]() . But before going into these,
we consider the magic square constructions of the Lie algebra
. But before going into these,
we consider the magic square constructions of the Lie algebra ![]() .
Vinberg's construction gives
.
Vinberg's construction gives
Starting from the Barton-Sudbery construction and using the concrete
descriptions of ![]() and
and ![]() from equation
(3), we obtain
from equation
(3), we obtain
If we define ![]() to be the simply connected group with Lie algebra
to be the simply connected group with Lie algebra
![]() , it follows from results of Adams that the subgroup generated by
the Lie subalgebra
, it follows from results of Adams that the subgroup generated by
the Lie subalgebra
![]() is isomorphic to
is isomorphic to
![]() . This lets us define the bioctonionic
projective plane by
. This lets us define the bioctonionic
projective plane by
Since ![]() is compact, we can put an
is compact, we can put an ![]() -invariant Riemannian metric on the bioctonionic
projective plane by averaging any metric with respect to the action
of this group. It turns out [5] that the isometry group of this
metric is exactly
-invariant Riemannian metric on the bioctonionic
projective plane by averaging any metric with respect to the action
of this group. It turns out [5] that the isometry group of this
metric is exactly ![]() , so we have
, so we have
Summarizing, we have 6 octonionic descriptions of ![]() :
:
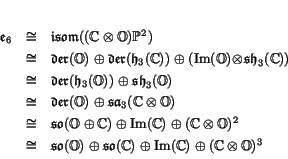
The smallest nontrivial representations of ![]() are 27-dimensional:
in fact it has two inequivalent representations of this dimension, which
are dual to one another. Now, the exceptional Jordan algebra is also
27-dimensional, and in 1950 this clue led Chevalley and Schafer [18]
to give a nice description of
are 27-dimensional:
in fact it has two inequivalent representations of this dimension, which
are dual to one another. Now, the exceptional Jordan algebra is also
27-dimensional, and in 1950 this clue led Chevalley and Schafer [18]
to give a nice description of ![]() as symmetries of this algebra.
These symmetries do not preserve the product, but only the determinant.
as symmetries of this algebra.
These symmetries do not preserve the product, but only the determinant.
More precisely, the group of determinant-preserving linear
transformations of ![]() turns out to be a noncompact real form of
turns out to be a noncompact real form of
![]() . This real form is sometimes called
. This real form is sometimes called ![]() , because its
Killing form has signature
, because its
Killing form has signature ![]() . To
see this, note that any automorphism of
. To
see this, note that any automorphism of ![]() preserves the
determinant, so we get an inclusion
preserves the
determinant, so we get an inclusion
We saw in Section 3.4 that the projective plane structure of
![]() can be constructed starting only with the determinant function
on the vector space
can be constructed starting only with the determinant function
on the vector space ![]() . It follows that
. It follows that ![]() acts as collineations on
acts as collineations on ![]() , that is, line-preserving
transformations. In fact, the group of collineations of
, that is, line-preserving
transformations. In fact, the group of collineations of ![]() is
precisely
is
precisely ![]() :
:
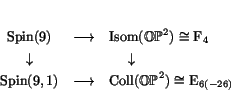
© 2001 John Baez