A basic test of general relativity is to check that it reduces to
good old Newtonian gravity in the limit where gravitational effects are
weak and velocities are small compared to the speed of light.
To do this, we can use our formulation of Einstein's equation
to derive Newton's inverse-square force law for a planet with mass ![]() and radius
and radius ![]() . Since we can only do this when gravitational effects
are weak, we must assume that the planet's radius is much greater than
its Schwarzschild radius:
. Since we can only do this when gravitational effects
are weak, we must assume that the planet's radius is much greater than
its Schwarzschild radius: ![]() in units where
in units where
![]() .
Then the curvature of space - as opposed to spacetime -
is small. To keep things simple, we make a couple of additional
assumptions: the planet has uniform density
.
Then the curvature of space - as opposed to spacetime -
is small. To keep things simple, we make a couple of additional
assumptions: the planet has uniform density ![]() , and the pressure
is negligible.
, and the pressure
is negligible.
We want to derive the familiar Newtonian result
To do this, let ![]() be a sphere of radius
be a sphere of radius ![]() centered on the planet. Fill
the interior of the sphere with test particles, all of which are initially
at rest relative to the planet. At first, this might seem like an
illegal thing to do: we know that notions like `at rest' only make sense
in an infinitesimal neighborhood, and
centered on the planet. Fill
the interior of the sphere with test particles, all of which are initially
at rest relative to the planet. At first, this might seem like an
illegal thing to do: we know that notions like `at rest' only make sense
in an infinitesimal neighborhood, and ![]() is not infinitesimal. But
because space is nearly flat for weak gravitational fields, we can
get away with this.
is not infinitesimal. But
because space is nearly flat for weak gravitational fields, we can
get away with this.
We can't apply our formulation of Einstein's equation directly to
![]() , but we can apply it to any infinitesimal sphere within
, but we can apply it to any infinitesimal sphere within
![]() . In the picture below, the solid black circle represents the
planet, and the dashed circle is
. In the picture below, the solid black circle represents the
planet, and the dashed circle is ![]() . The interior of
. The interior of ![]() has been
divided up into many tiny spheres filled with test particles. Green
spheres are initially inside the planet, and red spheres are outside.
has been
divided up into many tiny spheres filled with test particles. Green
spheres are initially inside the planet, and red spheres are outside.
![[01]](inversesquare1.gif)
Suppose we pick a tiny green sphere that lies within the planet's
volume, a distance less than ![]() from the center. Our formulation
of Einstein's equation
(2)
tells us that the fractional change in volume
of this sphere will be
from the center. Our formulation
of Einstein's equation
(2)
tells us that the fractional change in volume
of this sphere will be
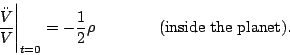

![[01]](inversesquare2.gif)
Because the volume occupied by the spheres of particles within
the planet went down, the whole big sphere of test particles had
to shrink. Now consider the following question:
what is the change in volume of the large sphere of test
particles? All the little green spheres shrank by the same fractional
amount:
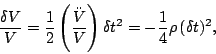
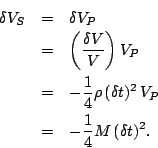
We can also express ![]() in terms of the change in
the sphere's radius,
in terms of the change in
the sphere's radius, ![]() :
:
© 2006 John Baez and Emory Bunn