To get M, we can also start with a 4-ball B4 and attach 8 copies of D2 × D2 to its boundary ∂B4 = S3. We attach these along solid tori as shown here:
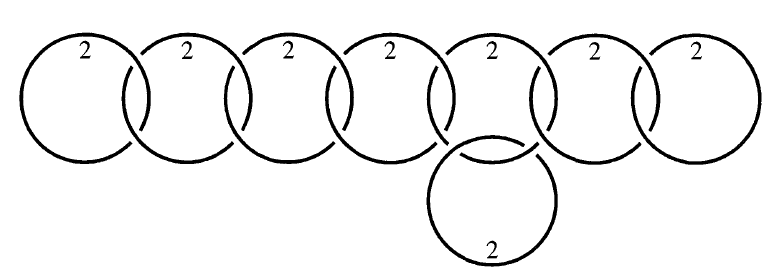
E8 again!
This is no coincidence: it's just a consequence of things we've already seen.
To get M, we can also start with a 4-ball B4 and attach 8 copies of D2 × D2 to its boundary ∂B4 = S3. We attach these along solid tori as shown here:

E8 again!
This is no coincidence: it's just a consequence of things we've already seen.
or
The picture of linked circles is from Section 8.3 here:
Another interesting thing you can learn about in Scorpan's book: the Poincaré homology sphere also bounds a topological (not smooth) 4-manifold with boundary that is contractible. Gluing this to M, we get a topological 4-manifold without any boundary. This is called the E8 manifold since the intersection pairing on its 2nd homology is the Cartan matrix of E8. This topological manifold cannot be smoothed!