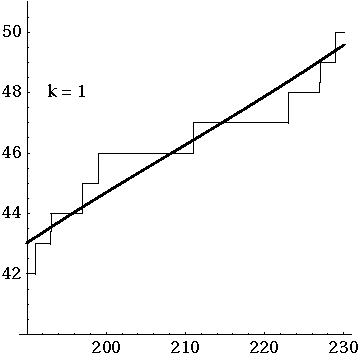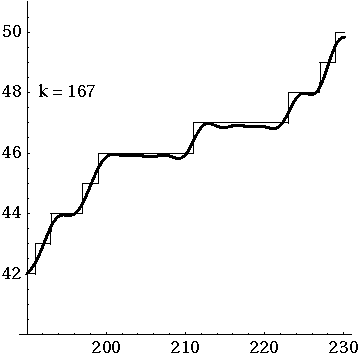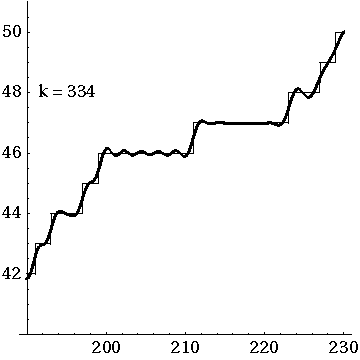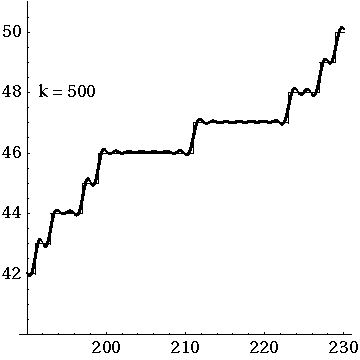

Underlying the Riemann Hypothesis there is a question whose full answer still eludes us: what do the zeros of the Riemann zeta function really mean? As a step toward answering this, André Weil proposed a series of conjectures that include a simplified version of the Riemann Hypothesis in which the meaning of the zeros becomes somewhat easier to understand. Grothendieck and others worked for decades to prove Weil's conjectures, inventing a large chunk of modern algebraic geometry in the process. This quest, still in part unfulfilled, led Grothendieck to dream of 'motives': mysterious building blocks that could explain the zeros (and poles) of Weil's analogue of the Riemann zeta function. This talk by a complete amateur will try to sketch some of these ideas in ways that other amateurs can enjoy.
Here's a video of this talk:
You can see my slides here — they're a series of webpages, so click "Next" to move on to the next slide.
You can also see my slides as a PDF, without the animations.
You can also read an expository paper I wrote based on this talk.