


|
|

|
We've been comparing two theories: stochastic mechanics and quantum mechanics. Last time we saw that any graph gives us an example of both theories! It's a bit peculiar, but today we'll explore the intersection of these theories a little further, and see that it has another interpretation. It's also the theory of electrical circuits made of resistors!
That's nice, because I'm supposed to be talking about 'network theory', and electrical circuits are perhaps the most practical networks of all:
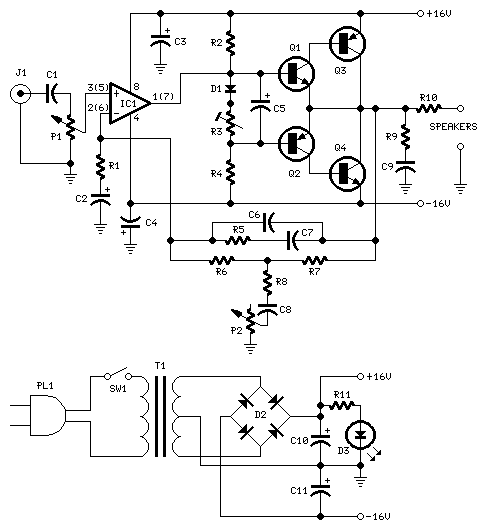
I plan to talk a lot about electrical circuits. I'm not quite ready to dive in, but I can't resist dipping my toe in the water today. Why don't you join me? It's not too cold!
and
That's sort of neat, so it's natural to wonder what are all the operators that are both infinitesimal stochastic and self-adjoint. They're called 'Dirichlet operators', and at least in the finite-dimensional case we're considering, they're easy to completely understand. Even better, it turns out they describe electrical circuits made of resistors!
Today let's take a lowbrow attitude and think of a linear operator $H : \mathbb{C}^n \to \mathbb{C}^n$ as an $n \times n$ matrix with entries $H_{i j}$. Then:
$$H_{i j} = \overline{H}_{j i}$$
$$\sum_i H_{i j} = 0$$
$$i \ne j \Rightarrow H_{i j} \ge 0 $$
What are Dirichlet operators like? Suppose $H$ is a Dirichlet operator. Then its off-diagonal entries are $\ge 0$, and since
$$ \sum_i H_{i j} = 0$$
its diagonal entries obey
$$ H_{i i} = - \sum_{ i \ne j} H_{i j} \le 0$$
So all the entries of the matrix $H$ are real, which in turn implies it's symmetric:
$$ H_{i j} = \overline{H}_{j i} = H_{j i} $$
So, we can build any Dirichlet operator $H$ as follows:
Note that because the entries are real, we can think of a Dirichlet operator as a linear operator $H : \mathbb{R}^n \to \mathbb{R}^n$. We'll do that for the rest of today.
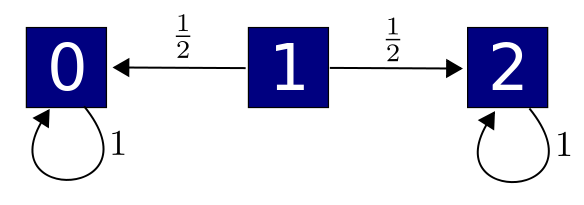
Now for the fun part. We can easily draw any Dirichlet operator! To this we draw $n$ dots, connect each pair of distinct dots with an edge, and label the edge connecting the $i$th dot to the $j$th with any number $H_{i j} \ge 0$.

This contains all the information we need to build our Dirichlet operator. To make the picture prettier, we can leave out the edges labelled by 0:

Like last time, the graphs I'm talking about are simple: undirected, with no edges from a vertex to itself, and at most one edge from one vertex to another. So:
Theorem. Any finite simple graph with edges labelled by positive numbers gives a Dirichlet operator, and conversely.
We already talked about a special case last time: if we label all the edges by the number 1, our operator $H$ is called the graph Laplacian. So, now we're generalizing that idea by letting the edges have more interesting labels.
What's the meaning of this trick? Well, we can think of our graph as an electrical circuit where the edges are wires. What do the numbers labelling these wires mean? One obvious possibility is to put a resistor on each wire, and let that number be its resistance. But that doesn't make sense, since we're leaving out wires labelled by 0. If we leave out a wire, that's not like having a wire of zero resistance: it's like having a wire of infinite resistance! No current can go through when there's no wire. So the number labelling an edge should be the conductance of the resistor on that wire. Conductance is the reciprocal of resistance.
So, our Dirichlet operator above gives a circuit like this:

Here Ω is the symbol for an 'ohm', a unit of resistance... but the upside-down version, namely ℧, is the symbol for a 'mho', a unit of conductance that's the reciprocal of an ohm.
Let's see if this cute idea leads anywhere. Think of a Dirichlet operator $H : \mathbb{R}^n \to \mathbb{R}^n$ as a circuit made of resistors. What could a vector $\psi \in \mathbb{R}^n$ mean? It assigns a real number to each vertex of our graph. The only sensible option is for this number to be the electric potential at that point in our circuit. So let's try that.
Now, what's
$$ \langle \psi, H \psi \rangle ?$$
In quantum mechanics this would be a very sensible thing to look at: it would be gives us the expected value of the Hamiltonian $H$ in a state $\psi$. But what does it mean in the land of electrical circuits?
Up to a constant fudge factor, it turns out to be the power consumed by the electrical circuit!
Let's see why. First, remember that when a current flows along a wire, power gets consumed. In other words, electrostatic potential energy gets turned into heat. The power consumed is
$$ P = V I $$
where $V$ is the voltage across the wire and $I$ is the current flowing along the wire. If we assume our wire has resistance $R$ we also have Ohm's law:
$$ I = V / R $$
so
$$ \displaystyle{ P = \frac{V^2}{R} } $$
If we write this using the conductance instead of the resistance, we get
$$ P = \textrm{conductance} \; V^2 $$
But our electrical circuit has lots of wires, so the power it consumes will be a sum of terms like this. We're assuming $H_{i j}$ is the conductance of the wire from the $i$th vertex to the $j$th, or zero if there's no wire connecting them. And by definition, the voltage across this wire is the difference in electrostatic potentials at the two ends: $\psi_i - \psi_j$. So, the total power consumed is
$$ \displaystyle{ P = \sum_{i \ne j} H_{i j} (\psi_i - \psi_j)^2 }$$
This is nice, but what does it have to do with $ \langle \psi , H \psi \rangle$?
The answer is here:
Theorem. If $H : \mathbb{R}^n \to \mathbb{R}^n$ is any Dirichlet operator, and $\psi \in \mathbb{R}^n$ is any vector, then
$$ \displaystyle{ \langle \psi , H \psi \rangle = -\frac{1}{2} \sum_{i \ne j} H_{i j} (\psi_i - \psi_j)^2 } $$
Proof. Let's start with the formula for power:
$$ \displaystyle{ P = \sum_{i \ne j} H_{i j} (\psi_i - \psi_j)^2 } $$
Note that this sum includes the condition $i \ne j$, since we only have wires going between distinct vertices. But the summand is zero if $i = j$, so we also have
$$ \displaystyle{ P = \sum_{i, j} H_{i j} (\psi_i - \psi_j)^2 }$$
Expanding the square, we get
$$ \displaystyle{ P = \sum_{i, j} H_{i j} \psi_i^2 - 2 H_{i j} \psi_i \psi_j + H_{i j} \psi_j^2 } $$
The middle term looks promisingly similar to $\langle \psi, H \psi \rangle$, but what about the other two terms? Because $H_{i j} = H_{j i}$, they're equal:
$$ \displaystyle{ P = \sum_{i, j} - 2 H_{i j} \psi_i \psi_j + 2 H_{i j} \psi_j^2 } $$
And in fact they're zero! Since $H$ is infinitesimal stochastic, we have
$$ \displaystyle{ \sum_i H_{i j} = 0 } $$
so
$$ \displaystyle{ \sum_i H_{i j} \psi_j^2 = 0 } $$
and it's still zero when we sum over $j$. We thus have
$$ \displaystyle{ P = - 2 \sum_{i, j} H_{i j} \psi_i \psi_j } $$
But since $\psi_i$ is real, this is -2 times
$$ \displaystyle{ \langle \psi, H \psi \rangle = \sum_{i, j} H_{i j} \overline{\psi}_i \psi_j } $$
So, we're done. █
An instant consequence of this theorem is that a Dirichlet operator has
$$ \langle \psi , H \psi \rangle \le 0 $$
for all $\psi$. Actually most people use the opposite sign convention in defining infinitesimal stochastic operators. This makes $H_{i j} \le 0$, which is mildly annoying, but it gives
$$ \langle \psi , H \psi \rangle \ge 0 $$
which is nice. When $H$ is a Dirichlet operator, defined with this opposite sign convention, $\langle \psi , H \psi \rangle$ is called a Dirichlet form.
Maybe it's a good time to step back and see where we are.
So far we've been exploring the analogy between stochastic mechanics and quantum mechanics. Where do networks come in? Well, they've actually come in twice so far:
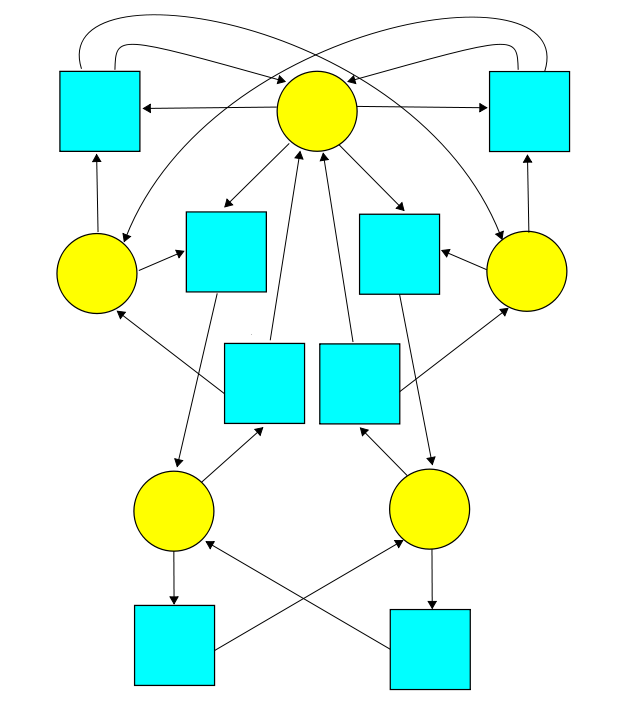
The different kinds of things are the yellow circles; we called them states, because sometimes we think of them as different states of a single kind of thing. The reactions where things turn into other things are the blue squares: we called them transitions. We label the transitions by numbers to say the rates at which they occur.
Now the dark blue boxes are states and the edges are transitions!
Today we looked at a special case of the second kind of network: the Dirichlet operators. For these the 'forward' transition rate $H_{i j}$ equals the 'reverse' rate $H_{j i}$, so our graph can be undirected: no arrows on the edges. And for these the rates $H_{i i}$ are determined by the rest, so we can omit the edges from vertices to themselves:

The result can be seen as an electrical circuit made of resistors! So we're building up a little dictionary:
This dictionary may seem rather odd—especially the third item, which looks completely different than the first two! But that's good: when things aren't odd, we don't get many new ideas. The whole point of this 'network theory' business is to think about networks from many different viewpoints and let the sparks fly!
Actually, this particular oddity is well-known in certain circles. We've been looking at the discrete version, where we have a finite set of states. But in the continuum, the classic example of a Dirichlet operator is the Laplacian $H = \nabla^2$. And then:
$$ \frac{d}{d t} \psi = \nabla^2 \psi $$
is fundamental to stochastic mechanics.
$$ \frac{d}{d t} \psi = -i \nabla^2 \psi $$
is fundamental to quantum mechanics.
$$ \nabla^2 \psi = -\rho $$
is fundamental to electrostatics.
Briefly speaking, electrostatics is the study of how the electric potential $\psi$ depends on the charge density $\rho$. The theory of electrical circuits made of resistors can be seen as a special case, at least when the current isn't changing with time.
I'll say a lot more about this... but not today! If you want to learn more, this is a great place to start:
• P. G. Doyle and J. L. Snell, Random Walks and Electrical Circuits, Mathematical Association of America, Washington DC, 1984.
This free online book explains, in a really fun informal way, how random walks on graphs, are related to electrical circuits made of resistors. To dig deeper into the continuum case, try:
• M. Fukushima, Dirichlet Forms and Markov Processes, North-Holland, Amsterdam, 1980.
You can also read comments on Azimuth, and make your own comments or ask questions there!

|
|

|