I will begin by stating the bare facts briefly, at the cost of some precision.
Any quantum-mechanical system possesses angular momentum, sometimes called
spin1.
Angular momentum is quantized, that is it is always an integer multiple of
![]() . (Here,
. (Here, ![]() , where
, where ![]() of course is Planck's
constant.) Traditionally,
of course is Planck's
constant.) Traditionally, ![]() stands for angular momentum2. If we use so-called natural units of measurement (and
we will), then
stands for angular momentum2. If we use so-called natural units of measurement (and
we will), then ![]() and possible values of
and possible values of ![]() are
are
![]() .
.
Say we measure the component of angular momentum along some axis, say the
![]() -axis. Let
-axis. Let ![]() stand for this component. 3 Then
stand for this component. 3 Then ![]() is also
quantized, and possible values for
is also
quantized, and possible values for ![]() are
are
The total magnitude of angular momentum is given by
![]() ; if this is measured somehow4, the result will be
; if this is measured somehow4, the result will be
![]() . In classical mechanics, we would get
. In classical mechanics, we would get ![]() and not
and not
![]() (as we will see in a moment).
(as we will see in a moment).
Suppose we combine two systems together, one with angular momentum ![]() ,
the other with angular momentum
,
the other with angular momentum ![]() . The resulting composite system will
have angular momentum equal to one of the values
. The resulting composite system will
have angular momentum equal to one of the values
This addition rule for angular momenta lies behind a wealth of physical
phenomena. A simple example: suppose an atom absorbs a photon. A photon
always has spin 1. Suppose the atom starts out in a state with ![]() .
After absorbing the photon, the atom must make a transition to a state with
.
After absorbing the photon, the atom must make a transition to a state with
![]() , or 2. The same conclusion holds when an atom emits a photon.
This three-way choice ultimately manifests itself as a triplet of spectral
lines.
, or 2. The same conclusion holds when an atom emits a photon.
This three-way choice ultimately manifests itself as a triplet of spectral
lines.
Now let's be a little more precise. In classical mechanics, angular
momentum is a vector, say j, with components ![]() in some
coordinate system, and magnitude
in some
coordinate system, and magnitude
![]() .
Any component, say
.
Any component, say ![]() , can range in value from
, can range in value from ![]() to
to ![]() .
.
In quantum mechanics, we have a (complex) Hilbert space of state-vectors
(say ![]() ) for any system. A state-vector
) for any system. A state-vector ![]() specifies a state of the
system, and
specifies a state of the
system, and ![]() and
and ![]() specify the same state if and only if
specify the same state if and only if ![]() for
some non-zero complex number
for
some non-zero complex number ![]() . Let
. Let ![]() be some classical, real-valued
variable that you can measure (like energy or momentum). The ``quantum
version'' of
be some classical, real-valued
variable that you can measure (like energy or momentum). The ``quantum
version'' of ![]() is a Hermitian operator on
is a Hermitian operator on ![]() . The eigenvalues of this
operator are the possible values you can get from measuring
. The eigenvalues of this
operator are the possible values you can get from measuring ![]() . The
quantum system has a definite value for
. The
quantum system has a definite value for ![]() if and only if the system is in
an eigenstate of the operator. If not, the act of measurement will serve
to cast the system into such an eigenstate, with probabilities that can be
computed by the rules of quantum mechanics.
if and only if the system is in
an eigenstate of the operator. If not, the act of measurement will serve
to cast the system into such an eigenstate, with probabilities that can be
computed by the rules of quantum mechanics.
Applying this prescription to angular momentum, we see that ![]() all must be Hermitian operators. It turns out now that the Hilbert space
of quantum states decomposes, in the most general case, into a direct sum:
all must be Hermitian operators. It turns out now that the Hilbert space
of quantum states decomposes, in the most general case, into a direct sum:
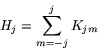
Each ![]() is of course invariant under
is of course invariant under ![]() , i.e., we have an
invariant direct-sum decomposition of
, i.e., we have an
invariant direct-sum decomposition of ![]() for the operator
for the operator ![]() . The
. The
![]() are not invariant under
are not invariant under ![]() or
or ![]() , but it turns out
that the
, but it turns out
that the ![]() are invariant under all three operators
are invariant under all three operators ![]() ,
, ![]() ,
and
,
and ![]() . Put another way, the invariant direct-sum decompositions for
. Put another way, the invariant direct-sum decompositions for
![]() and
and ![]() have the same
have the same ![]() 's but different
's but different ![]() 's.
's.
Finally, the operator
![]() is itself a Hermitian
operator; each
is itself a Hermitian
operator; each ![]() is an eigenspace, with eigenvalue
is an eigenspace, with eigenvalue ![]() .
.
This excursion into Hilbert spaces should make mathematically-minded folk
more comfortable with the catalog of ``spin facts''. The space ![]() is
just the space of states that have ``spin
is
just the space of states that have ``spin ![]() ''; the subspace
''; the subspace ![]() is
the space with component
is
the space with component ![]() along the
along the ![]() -axis. I haven't discussed the
combination rules; this translates into statements about the direct-sum
decomposition of tensor products. Nor have I explained the curious
appearence of the term
-axis. I haven't discussed the
combination rules; this translates into statements about the direct-sum
decomposition of tensor products. Nor have I explained the curious
appearence of the term ![]() ; this is bound up with the
non-commutativity of
; this is bound up with the
non-commutativity of ![]() ,
, ![]() ,
, ![]() .
.
Historically, the rules for spin came from playing with experimental data. The rules worked but remained mysterious. The birth of quantum mechanics came later, at the hands of Heisenberg, Schrödinger, and Dirac. Spin fell into place soon after that.
Quantum mechanics is mysterious, of course, as numerous philosophical treatises attest. But during the crucial period from Bohr's first great work (in 1913) to Heisenberg's discovery of matrix mechanics (in 1925), certain technical facts sowed confusion above and beyond the general quantum ``spookiness''. I will single out one of these for special attention: the spin of the electron. In 1926, Goudsmit and Uhlenbeck proposed (correctly) that the electron has spin one-half. Only integer spin quantum systems have classical counterparts, as we will see. The fractional spin of the electron lurked amid the general confusion during the heyday of the ``old quantum theory'' (1913-1925), bedevilling physicists. (Goudsmit and Uhlenbeck actually made their proposal in the language of the old quantum theory, not the newly minted quantum mechanics. The next year Pauli showed how to incorporate spin into quantum mechanics.)
In these notes, I will roam through the history of the old quantum theory, zeroing in on the adumbrations of modern quantum spin. (I will intersperse remarks on what the pioneers were ``really doing''.) I will not lay out the whole array of modern mathematical toys that makes Everything Clear. The reader whose appetite has been whetted must turn to standard textbooks for that. But I will try paint an impressionistic picture of the luminous synthesis, with a few broad brush strokes and one or two detailed pointillistic patches.
© 2001 Michael Weiss