The Hydrogen Atom, Then and Now

Let us look at a simple model of hydrogen atom: we neglect the spin of the proton and the electron, and relativistic effects. What remains is a point charge in an inverse-square force field-- the classical Kepler problem.

With these simplifications, the states of the hydrogen atom can be specified by giving three integer labels $(n,l,m)$, with:

$$\begin{eqnarray*} n & = & 1,2,\ldots\\ l & = & 0,1,\ldots, n-1\\ m & = & -l,-(l-1),\ldots,(l-1), l\\ \end{eqnarray*}$$

The labels $(n,l,m)$ are called quantum numbers, and made their debut in Sommerfeld's elliptical orbit model. They correspond to certain classical features of the orbit:

$$\begin{eqnarray*} n & \leftrightarrow & \rm\sqrt{semimajor\ axis}\\ l & \left... ...mentum\\ m & \leftrightarrow & \rm orientation\ of\ the\ orbit \end{eqnarray*}$$

Sommerfeld's quantum conditions stated that these three classical quantities were restricted to integer values (and in fact the collection of values given above).⁶ I should really say ``integer multiples of $\hbar$'', but from now on I will adopt so-called natural units of measurement, which are chosen so that $\hbar=1$.

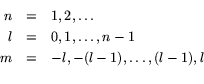
I should make one refinement to this description of the ``old quantum'' viewpoint. The quantum conditions apply only to so-called stationary orbits. Bohr offered no details for what happened during a transition from one stationary orbit to another (a ``quantum jump''), nor could he explain why these orbits were stationary. Initially, physicists probably regarded these questions as topics for future research.

In the post-1925 reformulation, we have to solve a particular instance of Schrödinger's equation, subject to certain boundary conditions. The space of all solutions is a Hilbert space, with a basis $\{v_{nlm}\}$. The vector $v_{nlm}$ is simultaneously an eigenvector of three operators:

$E$, the energy
$L$, the magnitude of the orbital angular momentum
$L_z$, the $z$-component of the orbital angular momentum

So we can say that if the hydrogen atom is in state $v_{nlm}$, then it has a definite energy, and its angular momentum has a definite magnitude and $z$-component. In fact, the eigenvalues for $v_{nlm}$ are:

$$\begin{eqnarray*} E v_{nlm} & = & \frac{R}{n^2}v_{nlm}\\ L v_{nlm} & = & \sqrt{l(l+1)}v_{nlm}\\ L_z v_{nlm} & = & m v_{nlm}\\ \end{eqnarray*}$$

where $R$ is a physical constant known as Rydberg's constant.

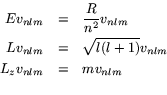
The modern equivalent of the old notion of ``stationary orbit'' is ``eigenstate of the energy operator''. Such eigenstates do not change with time, and they possess a definite value for the energy. (These facts are closely related.) Schrödinger's equation, in fact, amounts to $Ev=\lambda v$, where $E$ is the energy operator.

Figure 1: Term Scheme for Hydrogen

Figure 1 gives a pictorial representation of the basis $\{v_{nlm}\}$ in a form known as a term scheme. The horizontal lines stand for basis vectors (or equivalently, stationary quantum states); height gives energy, and transitions are indicated by slanted lines. (Only three transitions are pictured, to avoid clutter.)

From this simple diagram, many treasures flow. The next few paragraphs give a taste.

© 2001 Michael Weiss

home