|
|
|
|
Math is eternal, but I'll start with some news that may be time-sensitive. Betelgeuse is shrinking!
1) Stefan Scherer, Shrinking Betelgeuse, http://backreaction.blogspot.com/2009/06/shrinking-betelgeuse.html
Betelgeuse is that big red star in the shoulder of Orion. It's a red supergiant, one of the largest stars known. It's only 20 times the mass of the Sun, but it's about 1000 times as big across - about 5 times the size of the Earth's orbit. For more of a sense of what that means, watch this video. If you've got kids, have them watch it too:
2) Hansie0Slim, Largest stars this side of the Milky Way, http://www.youtube.com/watch?v=u70UBs7BWY8
But, it's shrinking. These authors claim its radius has shrunk 15% since 1993:
3) C. H. Townes, E. H. Wishnow, D. D. S. Hale and B. Walp, A systematic change with time in the size of Betelgeuse, The Astrophysical Journal Letters 697 (2009), L127-L128.
That's about 1000 kilometers per hour!
Of course, it's a bit tricky to estimate the size of Betelgeuse - besides being rather far, it's so diffuse that its surface isn't very precisely defined. And it's a variable star, so maybe a little shrinkage isn't a big deal. But the two known cycles governing its oscillations have periods of one year and 6 years. So, the authors of the above paper think this longer-term shrinkage has some other cause.
It could be just another cycle, with a longer period. But there's another possibility that's a lot more exciting. Maybe Betelgeuse is about to collapse and go supernova!
Indeed this seems likely in the long term, since that's the usual fate of such massive stars. And the long term may not even be so long, since Betelgeuse is about 8.5 million years old - quite old for stars this big, which live fast and go out in a blaze of glory.
What if Betelgeuse went supernova? How would it affect the US economy, and the next Presidential election? Could this be the Republican party's best hope?
Sorry, I'm being a bit parochial... let me try that again. How would it affect the insignificant inhabitants of a puny speck called Earth, located about 500 or 600 light years away from Betelgeuse? According to Brad Schaefer at Louisiana State University, it would be "brighter than a million full moons", but it wouldn't hurt us - in part because of the distance, and in part because we're not lined up with its pole.
(Perhaps just to build up the suspense, Schaefer added that Betelgeuse could already have gone supernova, in which case we're just waiting for its light to reach us.)
Actually, I have trouble believing that Betelgeuse gone supernova would be brighter than a million full moons. First of all, the full moon is 1/449,000 times as bright as the Sun. So, "brighter than a million full moons" is just an obscure way of saying "more than twice as bright as the Sun."
Second, let's try the calculation ourselves. There are various kinds of supernovae, with different luminosities. I guess Betelgeuse is most likely to become a type II supernova. Such supernovae show quite a bit of variation in their behavior. But anyway, it seems they get to be 1 billion times as bright as the Sun, or maybe at most - let's look at a worst-case scenario - 10 billion times as bright. So, between 109 and ten times that.
On the other hand, Betelgeuse is about 600 light years away, and there are 63,239 astronomical units in a light year, so it's about
600 × 63,000 ≅ 4 × 107
times as far away as the Sun - no point trying to be too precise here. Brightness scales as one over distance squared, so supernova Betelgeuse should look between
109 / (4 × 107)2 ≅ 7 × 10-7
as bright as the Sun, and ten times that bright.
As I mentioned, the full Moon is about 2 × 10-6 times as bright as the Sun. So, supernova Betelgeuse should be roughly between 1/3 as bright as the full Moon, and 3 times as bright. This is a rough calculation, but I've done it a few different ways and gotten similar answers. So, it's safe to say that "brighter than a million full moons" is a vast exaggeration.
Whew.
It's worth recalling that not too long ago, a supernova exploded at a roughly comparable distance from us, forming the "Local Bubble" - a peanut-shaped region of hot thin gas about 300 light years across, containing our Sun. The gas in the Local Bubble is about 1000 times less dense than ordinary interstellar space, and vastly hotter.
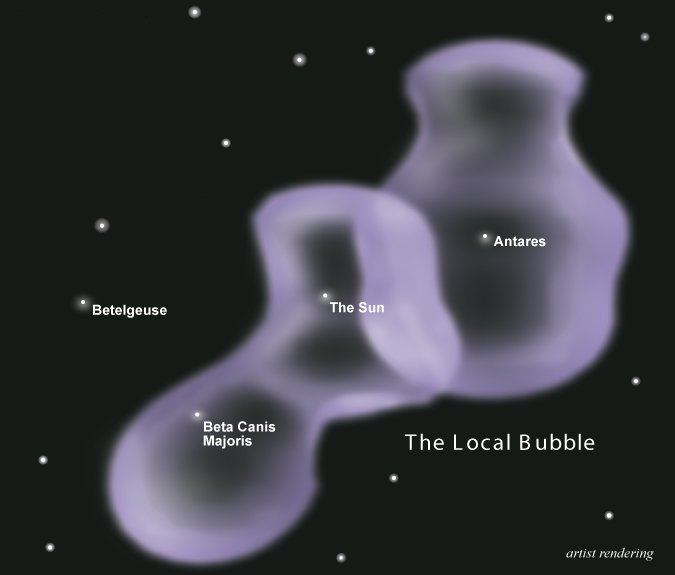
What do I mean by "not too long ago"? Well, nobody is sure, but back in "week144" I reported a bunch of evidence for a theory that the Local Bubble was formed just 340,000 years ago, when a star called Geminga went supernova, perhaps 180 light years away.
Now I'm getting a sense that the situation is more complex. It seems our Sun is near the boundary of the Local Bubble and another one, called the "Loop I Bubble". This other bubble seems to have formed earlier - perhaps 2 million years ago, at the Pliocene-Pleistocene transition, when a bunch of ultraviolet-sensitive marine creatures mysteriously died:
4) NASA, Near-earth supernovas, http://science.nasa.gov/headlines/y2003/06jan_bubble.htm
The Loop I Bubble may have been caused by a supernova in "Sco-Cen", a cloud in the directions of Scorpius and Centaurus. It's about 450 light years away now, but it used to be considerably closer.
In the last few million years, some wisps of interstellar gas have drifted into the Local Bubble. Our solar system is immersed in one of these filaments, charmingly dubbed the "local fluff". It's much cooler than the hot gas of the Local Bubble: 7000 Kelvin instead of roughly 1 million. It's also much denser - about 0.1 atoms per cubic centimeter instead of 0.05 or so. But Sco-Cen is sending interstellar cloudlets in our direction that are denser still, by a factor of 100. These might actually have some effect on the Sun's magnetic field when they reach us.
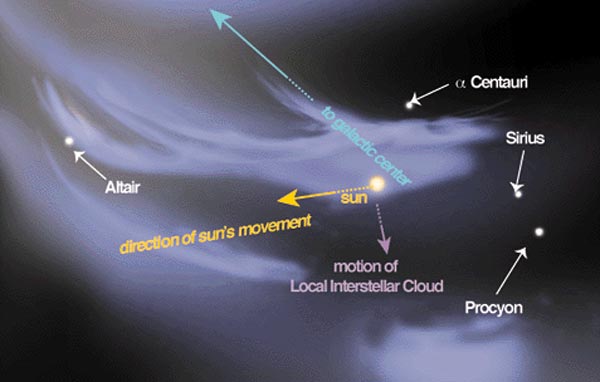Map of the local interstellar medium within 10 years of the Sun, I'm sure we'll get a clearer story as time goes by. In 2003, NASA launched a satellite called the Cosmic Hot Interstellar Plasma Spectrometer, or CHIPS for short, to study this sort of thing:
5) NASA/UC Berkeley, Overview of CHIPS Science, http://chips.ssl.berkeley.edu/science.html
It sounds pretty interesting. Unfortunately the latest news on the CHIPS homepage dates back to 2005, before they'd done much science. What's up?
You can't do much about Betelgeuse. But you can do something about mathematics! For example, if you're into categories or n-categories, you can help out the nLab:
6) nLab, http://ncatlab.org/nlab
The nLab is like the library, or laboratory, in the back room of the n-Category Café. The nCafé is a place to chat: it's a blog. The nLab is a place to work: it's a wiki. It's been operating since November 2008. There's quite a lot there by now, but it's really just getting started.
Check it out! You'll find explanations of many concepts, which you may be able to improve, and the beginnings of some big projects, which you may want to join.
So far the main contributors include Urs Schreiber, Mike Shulman, Toby Bartels, Tim Porter, Ronnie Brown, Todd Trimble, David Roberts, Andrew Stacey, Bruce Bartlett, Zoran Škoda, Eric Forgy and myself. Jim Dolan recently joined in with a page on algebraic geometry for category theorists - I'll say more about this someday. And like the nCafé, technical aspects of the nLab are largely run by Jacques Distler - it uses some wiki software called Instiki which he is helping develop.
Finally, a bit of actual math. Here's a paper by the fellow I'm working with here in Paris, and a grad student of his:
7) Paul-André Mélliès and Nicolas Tabareau, Free models of T-algebraic theories computed as Kan extensions, available at http://hal.archives-ouvertes.fr/hal-00339331/fr/
I really need to understand this for my work with Mike Stay.
In "week200" I talked about Lawvere's work on algebraic theories; I'll assume you read that and pick up from there. In its narrowest sense, an "algebraic theory" is a category with finite products where every object is a product of copies of some fixed object c. We use algebraic theories to describe various types of mathematical gadgets: to be precise, any type of gadget that consists of a set with a bunch of n-ary operations satisfying a bunch of purely equational laws.
For any type of gadget like this, there's an algebraic theory C; I explained how you get this back in "week200". If we have a functor
F: C → Set
that preserves finite products, then F(c) becomes a specific gadget of the given type. Conversely, any specific gadget of the given type determines a functor like this.
So, we define a "model" of the theory C to be a functor
F: C → Set
that preserves finite products. But actually, this is just a model of C in the world of sets! We could replace Set by any other category with finite products, say X, and define a "model of the theory C in the environment X" to be a functor
F: C → X
that preserves finite products.
For example, if C is the theory of groups and X is Set, a model of C in X is a group. If instead X is the category of topological spaces, a model of C in X is a topological group. And so on. In general people call a model of this particular theory C in any old X a "group object in X".
But as you might fear, we want to understand more than a single model of C in X. As category theorists, we want to understand the whole category of models of C in X. This category, which I'll call Mod(C,X), has:
For example, if C is the theory of groups and X is the category of topological spaces, Mod(C,X) is the category of topological groups and continuous homomorphisms.
So far I've just been reviewing at a fast pace. What happens next? Well, there's always a forgetful functor
R: Mod(C,X) → X
sending any model to its underlying object in X. But what we'd really like is for R to have a left adjoint
L: X → Mod(C,X)
sending any object of X to the free gadget on that object. Then we could follow L by R to get a functor
RL: X → X
called a "monad". One reason this would be great is that monads are another popular way to study algebraic gadgets. I explained monads very generally back in "week89", and said how to get them from adjoint functors in "week92"; in "week257" I gave some links to some great videos by the Catsters explaining monads and what they're good for. So, I won't say more about monads now: I'll just assume you love them. Given this, you must be dying to know when the functor R has a left adjoint.
In fact it does whenever X has colimits that distribute over the finite products! For example, it does when X = Set. And Mélliès and Tabareau give a very nice modern explanation of this fact before generalizing the heck out of it.
The key is to note that
R: Mod(C,X) → X
is just an extreme case of forgetting some of the structure on an algebraic gadget: namely, forgetting all of it. More generally, suppose we have any map of algebraic theories
Q: B → C
that is, a finite-product-preserving functor that sends the special object b in B to the special object c in C. Then composition with Q gives a functor
Q*: Mod(C,X) → Mod(B,X)
For example, if B is the theory of groups and C is the theory of rings, C is "bigger", so we get an inclusion
Q: B → C
and then Q* is the functor that takes a ring object in X and forgets some of its structure, leaving us a group object in X. But when B is is the most boring algebraic theory in the world, the "theory of a bare object", then Q* forgets everything: it's our forgetful functor
R: Mod(C,X) → Mod(B,X) = X
So, we should ask quite generally when any functor like
Q*: Mod(C,X) → Mod(B,X)
has a left adjoint. And, the answer is: it always does!
The proof uses a left Kan extension followed by what Mélliès and Tabaraeu call a "miracle" - see page 5 of their paper. And, it's this miracle they want to understand and generalize.
Here's the basic idea. If we write Hom(C,X) for the category with
Hom(C,X) → Hom(B,X)
and this has a left adjoint
Hom(B,X) → Hom(C,X)
using a well-known trick called "Kan extension", or more precisely "left Kan extension". Since Mod(B,X) is included in Hom(B,X), we can compose this inclusion with the functor above:
Mod(B,X) → Hom(B,X) → Hom(C,X)
And now comes the miracle: this composite functor actually lands us in Mod(C,X), which sits inside Hom(C,X). This gives us a functor
Mod(B,X) → Mod(C,X)
which turns out to be what we wanted: the left adjoint of
Q*: Mod(C,X) → Mod(B,X)
Kan extensions are a very general concept, so the hard part is understanding and generalizing this miracle.
To do this Mélliès and Tabareau first generalize algebraic theories to "T-algebraic theories" where T is any pseudomonad on Cat. I already said that monads are a trick for studying very general algebraic gadgets. Similarly, pseudomonads are a trick for studying very general categorified algebraic gadgets, like "categories with finite products" or "monoidal categories" or "braided monoidal categories" or "symmetric monoidal categories".
Each of these types of categories allows us to define a type of "theory":
8) John Baez, Universal algebra and diagrammatic reasoning, available as http://math.ucr.edu/home/baez/universal/
Take my word for it: they're great. In particular, they're more "quantum" in flavor than algebraic theories. So, we would like to generalize Lawvere's original results to these other kinds of theories, which are all examples of "T-algebraic theories". But, it's not automatic! For example, it doesn't always work with PROPs.
A typical kind of algebraic gadget we could define with a PROP is a "bialgebra". While there's always a free group on a set, there's not usually a free bialgebra on a vector space! The problem is not the category of vector spaces: it's that bialgebras have not only "operations" like multiplication, but also "co-operations" like comultiplication.
So, Mélliès and Tabareau have their work cut out for them. But they tackle it very elegantly, using profunctors and a certain generalization thereof: Richard Wood's concept of "proarrow equipment". This lets them generalize the "miracle" to any situation where we have a little T-algebraic theory sitting inside a bigger one
Q: B → C
and the bigger one only has extra operations, not co-operations.
"Proarrow equipment" sounds pretty scary - it's taken me about a decade to overcome my fear of it. So I'll stop my summary here, right around page 12 of the paper - right when the fun is just getting started!
Addenda: Charles McElwain kindly responded to my plea for information about what would happen if Betelgeuse went supernova. He wrote:
As you mention, there's not a lot of (quality) work out there. Most of what I found briefly would score fairly high on the "crank index".Using this and other information, I checked that if Betelguese went supernova, it would not be anywhere nearly as bright as "a million full moons".Of course, near supernovas have a positive and essential role in life on earth, in there *being* an earth, rather than just a star...
A few that I found that weren't immediately eliminated as cranks, that might repay further investigation:
9) Michael Richmond, Will a nearby supernova endanger life on Earth?, Available at http://stupendous.rit.edu/richmond/answers/snrisks.txt
Perhaps the closest to the number-crunching you're looking for.
10) S. E Thorsett, Terrestrial implications of cosmological gamma-ray burst models, Astrophys. J. 444 (1995), L53. Also available as arXiv:astro-ph/9501019.
Specifically, nitric oxide increases/ozone decreases.
11) Steven I. Dutch, Life (briefly) near a supernova, Journal of Geoscience Education, 2005. Available at http://nagt.org/files/nagt/jge/abstracts/Dutch_v53n1.pdf
The conceit here is what would happen if the Sun went supernova; acknowledged as impossible, but a very interesting exercise almost as a "Fermi problem", spinning out the real implications of the classic Arthur C. Clarke story "Rescue Party", and interesting also pedagogically.
You can see one of my calculations above.
Andrew Platzer looked into what happened to CHIPS, the satellite that was supposed to study hot gas in the Local Bubble. And, he found a fascinating newspaper article about this satellite's quixotic, sad, but ultimately rather mysterious quest. Andrew wrote:
I am interested in space and I did a little bit of googling about the CHIP satellite. Turns out it was turned off about a year ago after a 5 year mission. Unfortunately, it never detected the UV signal of the local bubble according to the article. There's a full story in local California newspaper:12) Chris Thompson, Goodbye Mr. CHIPS, East Bay Express, July 2, 2008. Also available at http://www.eastbayexpress.com/ebx/PrintFriendly?oid=780923
And a couple of papers in the arxiv by M. Hurwitz referencing CHIPS; the more recent one is about spectra of comets:
13) M. Hurwitz, T. P. Sasseen and M. M. Sirk, Observations of diffuse EUV emission with the Cosmic Hot Interstellar Plasma Spectrometer (CHIPS), Astrophys. J. 623 (2005), 911-916. Also available as arXiv:astro-ph/0411121
14) T. P. Sasseen, M. Hurwitz et al, A search for EUV emission from comets with the Cosmic Hot Interstellar Plasma Spectrometer (CHIPS), Astrophys. J. 650 (2006), 461-469. Also available as arXiv:astro-ph/0606466.
The null result seems interesting since a signal was expected.
Still up there. TLE from NORAD:
CHIPSAT 1 27643U 03002B 09177.47579469 .00000388 00000-0 34685-4 0 1094 2 27643 94.0213 313.0310 0014359 84.1512 276.1301 14.97271142352353Andrew Platzer
"TLE" refers to the "two-line element" format for transmitting satellite locations.
The short version of the CHIPS story - which completely leaves out all the fascinating twists and turns you'll find in that newspaper article above - is that this satellite failed to detect the extreme ultraviolet radiation (EUV) that people expected from the hot gas of the Local Bubble. It doesn't seem like a malfunction. So, something we don't understand is going on!
Todd Trimble gave a snappy proof that the forgetful functor from bialgebras to vector spaces has no left adjoint. If it did, it would need to preserve limits. In particular, it would send the terminal bialgebra to the terminal vector space. But the terminal bialgebra is 1-dimensional, while the terminal vector space is 0-dimensional - a contradiction.
For more discussion visit the n-Category Café.
The question you raise, "how can such a formulation lead to computations?" doesn't bother me in the least! Throughout my whole life as a mathematician, the possibility of making explicit, elegant computations has always come out by itself, as a byproduct of a thorough conceptual understanding of what was going on. Thus I never bothered about whether what would come out would be suitable for this or that, but just tried to understand - and it always turned out that understanding was all that mattered. - Grothendieck
© 2009 John Baez
baez@math.removethis.ucr.andthis.edu
|
|
|
|