




|
 
|

|
I should be finishing up some more papers, but let me take a little break, and tell you about an old dream that's starting to come true. People are finally starting to understand extended topological quantum field theories using n-categories!
Back in 1995, Jim Dolan and I argued that n-dimensional extended TQFTS were representations of a certain n-category called nCob in which:
And, we thought we could glimpse a purely algebraic description of nCob. We called this the "cobordism hypothesis", and we explained it here:
1) John Baez and James Dolan, Higher-dimensional algebra and topological quantum field theory, J. Math. Phys. 36 (1995), 6073-6105. Also available as q-alg/9503002.
I talked about this back in "week49". For more, try these talks:
2) Eugenia Cheng, n-Categories with duals and TQFT, 4 lectures at the Fields Institute, January 2007. Audio available at http://www.fields.utoronto.ca/audio/06-07/#crs-ncategories and lecture notes by Chris Brav at http://math.ucr.edu/home/baez/fields/eugenia.pdf
Now Jacob Lurie has come out with a draft of an expository paper that outlines a massive program, developed with help from Mike Hopkins, to reformulate the cobordism hypothesis using more ideas from homotopy theory, and prove it:
3) Jacob Lurie, On the classification of topological field theories, available as arXiv:0905.0465.
He's running around giving talks about this work, and you can see some here:
4) Jacob Lurie, TQFT and the cobordism hypothesis, four lectures at the Geometry Research Group of the University of Texas at Austin, January 2009. Videos available at http://lab54.ma.utexas.edu:8080/video/lurie.html and lecture notes by Braxton Collier, Parker Lowrey and Michael Williams at http://www.ma.utexas.edu/users/plowrey/dev/rtg/notes/perspectives_TQFT_notes.html
Excited by this new progress, I decided to run around giving some talks about it myself - just to explain the basic intuitions to people who'd never thought about this stuff before. You can see my slides here:
5) John Baez, Categorification and topology, available at http://math.ucr.edu/home/baez/cat/
A key feature of Lurie's approach is that instead of using n-categories he uses (∞,n)-categories, which are ∞-categories where everything is invertible above dimension n. This is what gets ideas from homotopy theory into the game. I should talk about this more someday.
Meanwhile, Chris Schommer-Pries has written a thesis on 2d extended TQFTs which follows an approach much closer to what Jim and I had originally imagined. You could say he gives more of an individually hand-crafted treatment of the n = 2 case, as compared with Lurie's high-tech industrial approach that clobbers all n at once:
6) Chris Schommer-Pries, The Classification of Two-Dimensional Extended Topological Field Theories, Ph.D. theis, U.C. Berkeley, 2009. Available at http://sites.google.com/site/chrisschommerpriesmath/
Instead of (∞,n)-categories, Schommer-Pries just uses n-categories - and since he's doing 2d TQFTs, that means 2-categories. Or more precisely, "weak" 2-categories, where all the laws hold only up to equivalence. Like most people, he calls these "bicategories". And one of the charms of his thesis is that he gives a detailed treatment of the n = 2 column of the periodic table of n-categories - which in his language looks like this:
k-tuply monoidal n-categories
n = 0 n = 1 n = 2
k = 0 sets categories bicategories
k = 1 monoids monoidal monoidal
categories bicategories
k = 2 commutative braided braided
monoids monoidal monoidal
categories bicategories
k = 3 " " symmetric sylleptic
monoidal monoidal
categories bicategories
k = 4 " " " " symmetric
monoidal
bicategories
k = 5 " " " " " "
A k-tuply monoidal n-category is an (n+k)-category that's boring at the bottom k levels. For example, a category with just one object is a monoid. As we increase k, we get more and more commutative flavors of n-category. But after k hits n+2, we expect that increasing k further has no effect. At this point we say our n-category is "stable".
If the cobordism hypothesis is true, nCob is a stable n-category. For n = 2, such a gadget is often called a "symmetric monoidal bicategory". Schommer-Pries shows that 2Cob is indeed a symmetric monoidal bicategory. Even better, he gives a "generators and relations" description of this gadget, which is just the sort of thing we need for the 2d version of the cobordism hypothesis:
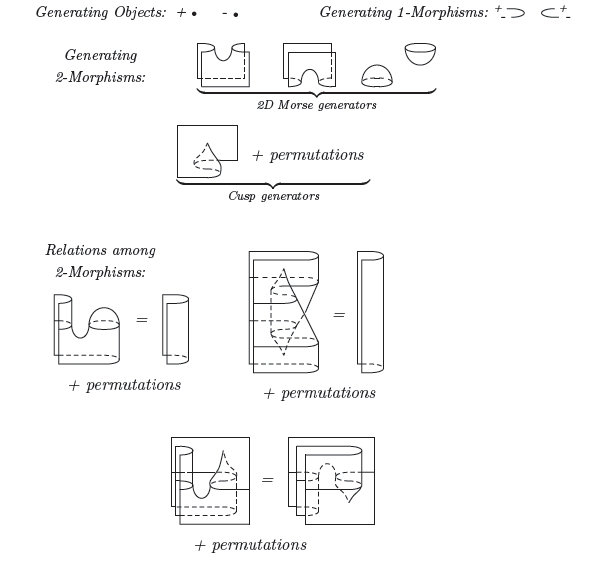
(Well, the really nice statement of the cobordism hypothesis involves framed oriented cobordisms, and we may need a topologist to tell us how those work - but there's also a version of the hypothesis for plain old oriented cobordisms, and that's what Schommer-Pries' thesis will give.)
For more on nCob as an n-category, try this:
7) Eugenia Cheng and Nick Gurski, Toward an n-category of cobordisms, Theory and Applications of Categories 18 (2007), 274-302. Available at http://www.tac.mta.ca/tac/volumes/18/10/18-10abs.html
I should add that a lot of the 2-category theory in Schommer-Pries' thesis relies on a thesis by a student of Ross Street:
8) Paddy McCrudden, Balanced coalgebroids, Theory and Applications of Categories 7 (2000), 71-147. Available at http://www.tac.mta.ca/tac/volumes/7/n6/7-06abs.html
Two students of mine should read the stuff about symmetric monoidal bicategories in this thesis! One is Alex Hoffnung, whose work on Hecke algebras uses the symmetric monoidal bicategory where:
The other is Mike Stay, whose work on computer science uses the symmetric monoidal bicategory where:
A profunctor is a categorified version of a matrix. More precisely, a profunctor from C to D is a functor
F: C × Dop → Set
so it's like a matrix of sets. A span of groupoids where the legs are fibrations is also a categorified version of a matrix, since by a theorem of Grothendieck we can reinterpret it as a weak 2-functor
F: C × Dop → Gpd
where now C and D are groupoids. So, both these students are studying aspects of "categorified matrix mechanics"... and we need symmetric monoidal bicategories to provide the proper context for such work. This should connect up to the 2d version of the cobordism hypothesis in some interesting ways.
As for your problems... I am so tired of mathematics and hold it in such low regard, that I could no longer take the trouble to solve them myself. - Descartes to Mersenne
© 2009 John Baez
baez@math.removethis.ucr.andthis.edu

|
 
|

|