2.3.2 Hypercharge and U(1)

In Section 2.2.2, we saw how to extend the notion of isospin to weak isospin, which proved to be more fundamental, since we saw in Section 2.3.1 how this gives rise to interactions among left-handed fermions mediated via $W$ bosons.

We grouped all the fermions into ${\rm SU}(2)$ representations. When we did this in Section 2.1, we saw that the ${\rm SU}(2)$ representations of particles were labeled by a quantity, the hypercharge $Y$, which relates the isospin $I_3$ to the charge $Q$ via the Gell-Mann-Nishijima formula

$$Q = I_3 + Y/2.$$

We can use this formula to extend the notion of hypercharge to weak hypercharge, a quantity which labels the weak isospin representations. For left-handed quarks, this notion, like weak isospin, coincides with the old isospin and hypercharge. We have weak hypercharge $Y = \frac{1}{3}$ for these particles:

$$\begin{array}{ccccrcr} Q(u_L) &=& I_3(u_L) + Y/2 & = & \frac... ...= & -\frac{1}{2}+ \frac{1}{6}& =& -\frac{1}{3}. \\ \end{array}$$

But just as weak isospin extended isospin to leptons, weak hypercharge extends hypercharge to leptons. For left-handed leptons the Gell-Mann-Nishijima formula holds if we set $Y = -1$:

$$\begin{array}{ccccrcr} Q(\nu_L) &=& I_3(\nu_L) + Y/2 & = & \... ...) + Y/2 & = & -\frac{1}{2}- \frac{1}{2}&=& -1 . \\ \end{array}$$

Note that the weak hypercharge of quarks comes in units one-third the size of the weak hypercharge for leptons, a reflection of the fact that quark charges come in units one-third the size of lepton charges. Indeed, thanks to the Gell-Mann-Nishijima formula, these facts are equivalent.

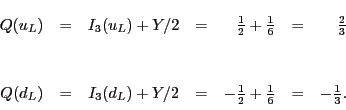
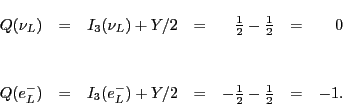
For right-handed fermions, weak hypercharge is even simpler. Since $I_3 = 0$ for these particles, the Gell-Mann-Nishijima formula reduces to

$$Q = Y/2.$$

So, the hypercharge of a right-handed fermion is twice its charge. In summary, the fermions have these hypercharges:

The First Generation of Fermions -- Hypercharge
Name	Symbol	$Y$
Left-handed leptons	$\left( \! \begin{array}{c} \nu_L \\ e^-_L \end{array} \! \right)$	$-1$
Left-handed quarks	$\left( \! \begin{array}{c} u_L \\ d_L \end{array} \! \right)$	$\frac{1}{3}$
Right-handed neutrino	$\nu_R$	$0$
Right-handed electron	$e^-_R$	$-2$
Right-handed up quark	$u_R$	$\frac{4}{3}$
Right-handed down quark	$d_R$	$-\frac{2}{3}$

But what is the meaning of hypercharge? We can start by reviewing our answer for the quantity $I_3$. This quantity, as we have seen, is related to how particles interact via $W$ bosons, because particles with $I_3 = \pm \frac{1}{2}$ span the fundamental representation of ${\rm SU}(2)$, while the $W$ bosons span the complexified adjoint representation, which acts on any other representation. Yet there is a deeper connection.

In quantum mechanics, observables like $I_3$ correspond to self-adjoint operators. We will denote the operator corresponding to an observable with a caret, for example $\hat{I}_3$ is the operator corresponding to $I_3$. A state of specific $I_3$, like $\nu_L$ which has $I_3 = \frac{1}{2}$, is an eigenvector,

$$\hat{I}_3 \nu_L = \frac{1}{2}\nu_L$$

with an eigenvalue that is the $I_3$ of the state. This makes it easy to write $\hat{I}_3$ as a matrix when we let it act on the ${\mathbb{C}}^2$ with basis $\nu_L$ and $e^-_L$, or any other doublet. We get

$$\hat{I}_3 = \left(\begin{array}{cc} \frac{1}{2}& 0 \\ 0 & -\frac{1}{2}\end{array} \right).$$

Note that this is an element of ${\mathfrak{su}}(2)$ divided by $i$. So, it lies in $\sl (2,{\mathbb{C}})$, the complexified adjoint representation of ${\rm SU}(2)$. In fact it equals $\frac{1}{2}W^0$, one of the gauge bosons. So, up to a constant of proportionality, the observable $\hat{I}_3$ is one of the gauge bosons!

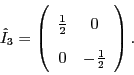
Similarly, corresponding to hypercharge $Y$ is an observable $\hat{Y}$. This is also, up to proportionality, a gauge boson, though this gauge boson lives in the complexified adjoint rep of ${\rm U}(1)$.

Here are the details. Particles with hypercharge $Y$ span irreps ${\mathbb{C}}_Y$ of ${\rm U}(1)$. Since ${\rm U}(1)$ is abelian, all of its irreps are one-dimensional. By ${\mathbb{C}}_Y$ we denote the one-dimensional vector space ${\mathbb{C}}$ with action of ${\rm U}(1)$ given by

$$\alpha \cdot z = \alpha^{3Y} z.$$

The factor of $3$ takes care of the fact that $Y$ might not be an integer, but is only guaranteed to be an integral multiple of $\frac{1}{3}$. For example, the left-handed leptons $\nu_L$ and $e^-_L$ both have hypercharge $Y = -1$, so each one spans a copy of ${\mathbb{C}}_{-1}$:

$$\nu_L \in {\mathbb{C}}_{-1}, \quad e^-_L \in {\mathbb{C}}_{-1}$$

or, more compactly,

$$\nu_L, e^-_L \in {\mathbb{C}}_{-1} \otimes {\mathbb{C}}^2$$

where ${\mathbb{C}}^2$ is trivial under ${\rm U}(1)$.

In summary, the fermions we have met thus far lie in these ${\rm U}(1)$ representations:

The First Generation of Fermions -- ${\rm U}(1)$ Representations
Name	Symbol	${\rm U}(1)$ rep
Left-handed leptons	$\left( \! \begin{array}{c} \nu_L \\ e^-_L \end{array} \! \right)$	${\mathbb{C}}_{-1}$
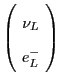Left-handed quarks	$\left( \! \begin{array}{c} u_L \\ d_L \end{array} \! \right)$	${\mathbb{C}}_{\frac{1}{3}}$
Right-handed neutrino	$\nu_R$	${\mathbb{C}}_{0}$
Right-handed electron	$e^-_R$	${\mathbb{C}}_{-2}$
Right-handed up quark	$u_R$	${\mathbb{C}}_{\frac{4}{3}}$
Right-handed down quark	$d_R$	${\mathbb{C}}_{-\frac{2}{3}}$

Now, the adjoint representation $\u (1)$ of ${\rm U}(1)$ is just the tangent space to the unit circle in ${\mathbb{C}}$ at 1. It is thus parallel to the imaginary axis, and can be identified as $i{\mathbb{R}}$. Is is generated by $i$. $i$ also generates the complexification, ${\mathbb{C}}\otimes \u (1) \cong {\mathbb{C}}$, though this also has other convenient generators, like 1. Given a particle $\psi \in {\mathbb{C}}_Y$ of hypercharge $Y$, we can differentiate the action of ${\rm U}(1)$ on $\psi$

$$e^{i\theta} \cdot \psi = e^{3iY\theta} \psi$$

and set $\theta = 0$ to find out how $\u (1)$ acts:

$$i \cdot \psi = 3iY \psi .$$

Dividing by $i$ we obtain

$$1 \cdot \psi = 3Y \psi .$$

In other words, we have

$$\hat{Y} = \frac{1}{3}\in {\mathbb{C}}$$

as an element of the complexified adjoint rep of ${\rm U}(1)$.

Particles with hypercharge interact by exchange of a boson, called the $B$ boson, which spans the complexified adjoint rep of ${\rm U}(1)$. Of course, since ${\mathbb{C}}$ is one-dimensional, any nonzero element spans it. Up to a constant of proportionality, the $B$ boson is just $\hat{Y}$, and we might as well take it to be equal to $\hat{Y}$, but calling it $B$ is standard in physics.

The $B$ boson is a lot like another, more familiar ${\rm U}(1)$ gauge boson--the photon! The hypercharge force which the $B$ boson mediates is a lot like electromagnetism, which is mediated by photons, but its strength is proportional to hypercharge rather than charge.