Next: 2.3.2 Hypercharge and U(1) Up: 2.3 The Fundamental Forces Previous: 2.3 The Fundamental Forces
The tale we told of isospin in Section 2.1 only concerned
the strong force, which binds nucleons together into nuclei. We learned
about an approximation in which nucleons live in the fundamental rep
![]() of the isospin symmetry group
of the isospin symmetry group ![]() , and that they interact by exchanging
pions, which live in the complexified adjoint rep of this group,
namely
, and that they interact by exchanging
pions, which live in the complexified adjoint rep of this group,
namely
![]() .
.
But this tale is mere prelude to the modern story, where weak isospin,
defined in Section 2.2.2, is the star of the show. This story
is not about the strong force, but rather the weak force. This story
parallels the old one, but it involves left-handed fermions instead of nucleons.
The left-handed fermions, with
![]() , are paired up into
fundamental representations of
, are paired up into
fundamental representations of ![]() , the weak isospin symmetry
group. There is one spanned by left-handed leptons:
, the weak isospin symmetry
group. There is one spanned by left-handed leptons:
Because these particles are paired up in the same ![]() representation,
physicists often write them as doublets:
representation,
physicists often write them as doublets:
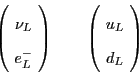
The particles in these doublets then interact via the exchange of ![]() bosons,
which are the weak isospin analogues of the pions. Like the pions, there are
three
bosons,
which are the weak isospin analogues of the pions. Like the pions, there are
three ![]() bosons:
bosons:
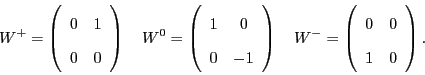
![\includegraphics[scale=0.75]{W+d_vertex}](img217.png)
Again, Feynman diagrams are the physicists' way of drawing
intertwining operators. Since all the
![]() 's are acted on by the same
's are acted on by the same
![]() , they can interact with each other via
, they can interact with each other via ![]() boson exchange. For
example, quarks and leptons can interact via
boson exchange. For
example, quarks and leptons can interact via ![]() 's:
's:
![\includegraphics[scale=0.75]{qlW_exchange}](img218.png)
![\includegraphics[scale=0.75]{betadecay}](img219.png)
The fact that only left-handed particles are combined into doublets reflects
the fact that only they take part in weak interactions. Every right-handed
fermion, on the other hand, is trivial under ![]() . Each one spans the
trivial rep,
. Each one spans the
trivial rep, ![]() . An example is the right-handed electron
. An example is the right-handed electron
In summary, left-handed fermions are grouped into doublets (nontrivial
representations of ![]() on
on
![]() ), while right-handed fermions are
singlets (trivial representations on
), while right-handed fermions are
singlets (trivial representations on ![]() ). So, the left-handed ones
interact via the exchange of
). So, the left-handed ones
interact via the exchange of ![]() bosons, while the right-handed ones do not.
bosons, while the right-handed ones do not.
| The First Generation of Fermions --
|
|||
| Name | Symbol | ||
| Left-handed leptons |
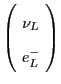 |
|
|
| Left-handed quarks |
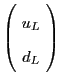 |
|
|
| Right-handed neutrino | |||
| Right-handed electron | |||
| Right-handed up quark | |||
| Right-handed down quark | |||
2010-01-11