Next: 3.3 The Pati-Salam Model Up: 3 Grand Unified Theories Previous: 3.1 The SU(5) GUT
We now turn our attention to another grand unified theory. Physicists
call it the `![]() theory', but we shall call it the
theory', but we shall call it the
![]() theory, because the Lie group involved is really
theory, because the Lie group involved is really
![]() , the double cover of
, the double cover of ![]() . This theory appeared in a
1974 paper by Georgi [10], shortly after his paper with
Glashow on the
. This theory appeared in a
1974 paper by Georgi [10], shortly after his paper with
Glashow on the ![]() theory. However, Georgi has said that he conceived
of the
theory. However, Georgi has said that he conceived
of the
![]() theory first. See Zee [40], Chapter VII.7,
for a concise and readable account.
theory first. See Zee [40], Chapter VII.7,
for a concise and readable account.
The ![]() GUT has helped us explain the pattern of hypercharges in the
Standard Model, and thanks to the use of the exterior algebra,
GUT has helped us explain the pattern of hypercharges in the
Standard Model, and thanks to the use of the exterior algebra,
![]() , we
can interpret it in terms of a binary code. This binary code explains another
curious fact about the Standard Model. Specifically, why is the number of
fermions a power of 2? There are 16 fermions, and 16 antifermions, which
makes the
Standard Model rep have dimension
, we
can interpret it in terms of a binary code. This binary code explains another
curious fact about the Standard Model. Specifically, why is the number of
fermions a power of 2? There are 16 fermions, and 16 antifermions, which
makes the
Standard Model rep have dimension
In actuality, however, the existence of a right-handed neutrino (or its antiparticle, the left-handed antineutrino) has been controversial. Because it transforms trivially in the Standard Model, it does not interact with anything except perhaps the Higgs.
The right-handed neutrino certainly improves the aesthetics of the
![]() theory. When we include this particle (and its antiparticle),
we obtain the rep
theory. When we include this particle (and its antiparticle),
we obtain the rep
More importantly, there is increasing indirect evidence from experimental particle physics that right-handed neutrinos do exist. For details, see Pati [27]. If this is true, the number of fermions really could be 16, and we have a ready-made explanation for that number in the binary code.
However, this creates a new mystery. The
![]() works nicely with the representation
works nicely with the representation
![]() , but
, but ![]() does
not require this. It works just fine with the smaller rep
does
not require this. It works just fine with the smaller rep
Let us look for a group that extends ![]() and has an irrep whose
dimension is some power of 2. The dimension is a big clue. What
representations have dimensions that are powers of 2? Spinors.
and has an irrep whose
dimension is some power of 2. The dimension is a big clue. What
representations have dimensions that are powers of 2? Spinors.
What are spinors? They are certain representations of ![]() ,
the double cover of the rotation group in
,
the double cover of the rotation group in ![]() dimensions, which do not factor
through the quotient
dimensions, which do not factor
through the quotient ![]() . Their dimensions are always a power of two.
We build them by exhibiting
. Their dimensions are always a power of two.
We build them by exhibiting ![]() as a subgroup of a
Clifford algebra. Recall that the Clifford algebra
as a subgroup of a
Clifford algebra. Recall that the Clifford algebra ![]() is
the associative algebra freely generated by
is
the associative algebra freely generated by
![]() with relations
with relations
We can use this method to get a rep of
![]() on
on
![]() that extends the rep of
that extends the rep of ![]() on this space.
In fact, quite generally
on this space.
In fact, quite generally
![]() acts on
acts on
![]() . Then, because
. Then, because
To see this, we use operators on
![]() called `creation and annihilation operators'. Let
called `creation and annihilation operators'. Let
![]() be the
standard basis for
be the
standard basis for
![]() . Each of these gives a creation operator:
. Each of these gives a creation operator:
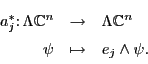
In physics, we can think of the basis vectors ![]() as particles.
For example, in the binary code approach to the
as particles.
For example, in the binary code approach to the ![]() theory we imagine five particles from which the observed
particles in the Standard Model are composed: up, down, red, green
and blue. Taking the wedge product with
theory we imagine five particles from which the observed
particles in the Standard Model are composed: up, down, red, green
and blue. Taking the wedge product with ![]() `creates a particle'
of type
`creates a particle'
of type ![]() , while the adjoint `annihilates a particle' of type
, while the adjoint `annihilates a particle' of type ![]() .
.
It may seem odd that creation is the adjoint of annihilation,
rather than its inverse. One reason for this is that the creation
operator, ![]() , has no inverse. In some sense, its adjoint
, has no inverse. In some sense, its adjoint ![]() is the best substitute.
is the best substitute.
This adjoint does do what want, which is to delete any particle of type
![]() . Explicitly, it deletes the `first' occurence of
. Explicitly, it deletes the `first' occurence of ![]() from any basis
element, bringing out any minus signs we need to make this respect the
antisymmetry of the wedge product:
from any basis
element, bringing out any minus signs we need to make this respect the
antisymmetry of the wedge product:
Now, whenever we have an inner product space like
![]() , we get an inner
product on
, we get an inner
product on
![]() . The fastest, if not most elegant, route to this inner
product is to remember that, given an orthonormal basis
. The fastest, if not most elegant, route to this inner
product is to remember that, given an orthonormal basis
![]() for
for
![]() , the induced basis, consisting of elements of the form
, the induced basis, consisting of elements of the form
![]() , should be orthonormal in
, should be orthonormal in
![]() . But choosing an
orthonormal basis defines an inner product, and in this case it defines an
inner product on the whole exterior algebra, one that reduces to the usual one
for the grade one elements,
. But choosing an
orthonormal basis defines an inner product, and in this case it defines an
inner product on the whole exterior algebra, one that reduces to the usual one
for the grade one elements,
![]() .
.
It is with respect to this inner product on
![]() that
that ![]() and
and ![]() are adjoint. That is, they satisfy
are adjoint. That is, they satisfy
These operators satisfy the following relations:
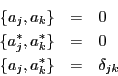
As an algebra,
![]() is generated by the standard basis vectors of
is generated by the standard basis vectors of
![]() . Let us call the elements of
. Let us call the elements of
![]() corresponding to these
basis vectors
corresponding to these
basis vectors
![]() . From the definition of
the Clifford algebra, is easy to check that
. From the definition of
the Clifford algebra, is easy to check that
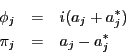
Now for ![]() we may define
we may define
![]() to be the universal cover of
to be the universal cover of
![]() , with group structure making the covering map
, with group structure making the covering map
![\begin{displaymath}
\xymatrix{
{\rm Spin}(2n) \ar[d]^p \\
{\rm SO}(2n)
}
\end{displaymath}](img506.png)
This construction of
![]() is fairly abstract. Luckily, we can realize
is fairly abstract. Luckily, we can realize
![]() as the multiplicative group in
as the multiplicative group in
![]() generated by products
of pairs of unit vectors. This gives us the inclusion
generated by products
of pairs of unit vectors. This gives us the inclusion
In fact, both these representations of
![]() are irreducible, and
are irreducible, and
![]() acts faithfully on their direct sum
acts faithfully on their direct sum
![]() . Elements of these
two irreps of
. Elements of these
two irreps of
![]() are called left- and right-handed
Weyl spinors, respectively, while elements of
are called left- and right-handed
Weyl spinors, respectively, while elements of
![]() are called
Dirac spinors.
are called
Dirac spinors.
All this works for any ![]() , but we are especially interested in the
case
, but we are especially interested in the
case ![]() . The big question is: does the Dirac spinor representation of
. The big question is: does the Dirac spinor representation of
![]() extend the obvious representation of
extend the obvious representation of ![]() on
on
![]() ?
Or, more generally, does the Dirac spinor representation of
?
Or, more generally, does the Dirac spinor representation of
![]() extend the representation of
extend the representation of ![]() on
on
![]() ?
?
Remember, we can think of a unitary representation as a group homomorphism
Proof. The complex vector space
![]() has an underlying
real vector space of dimension
has an underlying
real vector space of dimension ![]() , and the real part of the
usual inner product on
, and the real part of the
usual inner product on
![]() gives an inner product on this
underlying real vector space, so we have an inclusion
gives an inner product on this
underlying real vector space, so we have an inclusion
![]() . The connected component of the identity
in
. The connected component of the identity
in ![]() is
is ![]() , and
, and ![]() is connected, so this gives
an inclusion
is connected, so this gives
an inclusion
![]() and thus
and thus
![]() . Passing to Lie algebras,
we obtain an inclusion
. Passing to Lie algebras,
we obtain an inclusion
![]() .
A homomorphism of Lie algebras gives a homomorphism of the
corresponding simply-connected Lie groups, so this in turn gives
the desired map
.
A homomorphism of Lie algebras gives a homomorphism of the
corresponding simply-connected Lie groups, so this in turn gives
the desired map
![]() .
.
Next we must check that ![]() makes the above triangle commute.
Since all the groups involved are connected, it suffices to check
that this diagram
makes the above triangle commute.
Since all the groups involved are connected, it suffices to check
that this diagram
![\begin{displaymath}
\xymatrix{
{\mathfrak{su}}(n) \ar[r]^{d\psi} \ar[dr]_{d\rho}...
...k{so}}(2n) \ar[d]^{d\rho'} \\
& \u (\Lambda {\mathbb C}^n)
}
\end{displaymath}](img526.png)
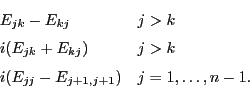
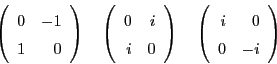
Now, it is easy to guess a formula for ![]() in terms of
creation and annihilation operators. After all, the
elementary matrix
in terms of
creation and annihilation operators. After all, the
elementary matrix ![]() satisfies
satisfies
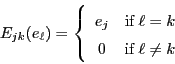
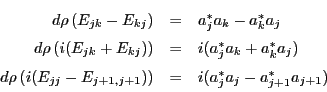
Now, the annihilation operators are a lot like derivations: they are
antiderivations. That is, if
![]() and
and
![]() , then
, then
So, ![]() can really be expressed in terms of annihilation and
creation operators as above. Checking that
can really be expressed in terms of annihilation and
creation operators as above. Checking that
![\begin{displaymath}
\xymatrix{
{\mathfrak{su}}(n) \ar[r]^{d\psi} \ar[dr]_{d\rho}...
...k{so}}(2n) \ar[d]^{d\rho'} \\
& \u (\Lambda {\mathbb C}^n)
}
\end{displaymath}](img526.png)
This theorem had a counterpart for the ![]() GUT--namely,
Theorem 1. There we saw a homomorphism
GUT--namely,
Theorem 1. There we saw a homomorphism ![]() that
showed us how to extend the Standard Model group
that
showed us how to extend the Standard Model group
![]() to
to ![]() , and
made this square commute:
, and
made this square commute:
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^\phi \ar[d] & {\rm SU...
...F^*) \ar[r]^-{{\rm U}(f)} & {\rm U}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img470.png)
![\begin{displaymath}
\xymatrix{
{\rm SU}(5) \ar[r]^{\psi} \ar[d]_\rho & {\rm Spin...
...bda {\mathbb C}^5) \ar[r]^1 & {\rm U}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img555.png)
![\begin{displaymath}
\xymatrix{
{G_{\mbox{\rm SM}}}\ar[r]^{\psi \phi} \ar[d] & {\...
... F^*) \ar[r]^-{{\rm U}(f)} & {\rm U}(\Lambda {\mathbb C}^5)
}
\end{displaymath}](img556.png)
2010-01-11